Dreifachzählung des SATOR-Quadrats
81 Buchstaben
1.
Die Untersuchung der
Palindromstruktur des SQ führt zu zwei Aussagen je Hälfte:
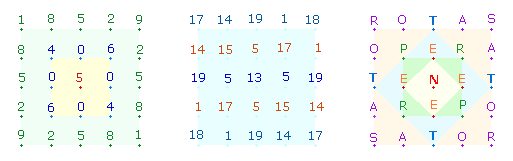
NET OPERA SATOR – Es webt die Werke der Schöpfer.
SATOR OPERA TENET (1) – Der Schöpfer erhält seine Werke.
TENET OPERA ROTAS (2) – er hält durch seine Sorge die Räder.
2.
Damit das Quadrat
nun nicht lediglich in zwei Teile zerfällt, binden die 5 Wörter des Quadrats die zweimal drei Wörter
zusammen.
Durch dreifache Zählung werden die 4 symmetrischen
Wörter je 3-mal und die Mittelachse
TENET viermal erfaßt, davon der
Mittelbuchstabe N fünfmal. Das ergibt an Buchstaben 3*4*5 = 60 + 4*5+1 = 21, zusammen 81 Buchstaben. Die Zahl 81 entspricht den 9*9 Zahlen der 1x1-Tabelle, aber besonders der Zahl der Elemente
des 5*5 Quadrats: 25 Punkte, 16 Quadrateinheiten + 40 Linien. Die Dreifachzählung liefert folgende Ergebnisse:
|
|
ZS |
*6 |
|
ZS |
*4 |
GS |
FS |
*6 |
|
FS |
*4 |
GS |
|
SATOR/ROTAS |
69 |
414 |
TENET |
61 |
244 |
|
54 |
324 |
TENET |
61 |
244 |
|
|
OPERA/AREPO |
52 |
312 |
1*N |
13 |
13 |
|
40 |
240 |
1*N |
|
13 |
|
|
|
|
726 |
|
|
257 |
983 |
|
564 |
|
|
257 |
821 |
|
983 = 7*139 |
||||||||||||
3.
Die 8 verschiedenen Buchstaben des SQ können zu dem Wort PENSATOR – der Ausgleichende geordnet werden. Die folgende Tabelle ermittelt die Häufigkeit
der 8 Buchstaben im Ausgangsquadrat von 25 Buchstaben:
|
|
P |
E |
N |
S |
sm |
A |
T |
O |
R |
sm |
GS |
|
ZW |
15 |
5 |
13 |
18 |
51 |
1 |
19 |
14 |
17 |
51 |
102 |
|
Hfk. |
2 |
4 |
1 |
2 |
9 |
4 |
4 |
4 |
4 |
16 |
25 |
|
ZS |
30 |
20 |
13 |
36 |
99 |
4 |
76 |
56 |
68 |
204 |
303 |
|
FS |
16 |
20 |
13 |
16 |
65 |
4 |
76 |
36 |
68 |
184 |
249 |
|
|
|
|
|
|
164 |
|
|
|
|
388 |
552 |
Die FW der ermittelten ZS+FS sind:
|
ZS |
99 |
204 |
303 |
FS |
65 |
184 |
249 |
|
FW |
17 |
24 |
41 |
FW |
18 |
29 |
47 |
|
|
116 |
228 |
344 |
|
83 |
213 |
296 |
|
296:344 = 8*(37:41) |
|||||||
37 und 41 bilden die Mitte der 26 Primzahlen von 1 bis 100.
4. Zu ermitteln ist nun die Häufigkeit der 8 Buchstaben in der Gesamtzahl von 81 Buchstaben:
|
|
P |
E |
N |
S |
sm |
A |
T |
O |
R |
Sm |
GS |
|
ZW |
15 |
5 |
13 |
18 |
51 |
1 |
19 |
14 |
17 |
51 |
102 |
|
Hfk. |
6 |
14 |
5 |
6 |
31 |
12 |
14 |
12 |
12 |
50 |
25 |
|
ZS |
90 |
70 |
65 |
108 |
333 |
12 |
266 |
168 |
204 |
650 |
983 |
|
FS |
48 |
70 |
65 |
48 |
231 |
12 |
266 |
108 |
204 |
590 |
821 |
|
|
138 |
140 |
130 |
156 |
564 |
24 |
532 |
276 |
408 |
1240 |
1804 |
|
1804 = 4*11*41; 564:1240 = 4*(141:310) |
|||||||||||
5. Daß die dreifache Sichtweise des SQ nicht einer phantasievollen Interpretation
entspricht, zeigt folgende Anordnung aller drei Versionen:
|
R |
O |
T |
A |
S |
|
O |
P |
E |
R |
A |
|
T |
E |
N|N |
E |
T |
|
A |
R |
E |
P |
O |
|
S |
A |
T |
O |
R |
|
R |
O |
T |
A |
S |
|
O |
P |
E |
R |
A |
|
T |
E |
N |
E |
T |
|
A |
R |
E |
P |
O |
|
S |
A |
T |
O |
R |
|
S |
A |
T |
O |
R |
|
O |
P |
E |
R |
A |
|
T |
E |
N |
E |
T |
|
T |
E |
N |
E |
T |
|
O |
P |
E |
R |
A |
|
R |
O |
T |
A |
S |
Die erste Version beginnt im Mittelpunkt: Jeweils ein N setzt sich nach rechts und links fort und wendet sich S-förmig der nächsten Zeile zu. Die zweite Version ist dieselbe mit nur einem N, die Leseweise ist traditionell von links nach rechts, bedarf aber der Interpretation durch S-förmigen Verlauf, die in der dritten Version von links nach rechts verwirklicht ist.
Jede der 5 Spalten enthält 16 Buchstaben, die mittlere 17. Die ZS+FS der 5 Spalten sind:
|
1 |
2 |
3 |
4 |
5 |
sm |
FW |
|
239 |
159 |
209 |
163 |
213 |
983 |
983 |
|
189 |
116 |
209 |
134 |
173 |
821 |
821 |
|
428 |
275 |
418 |
297 |
386 |
1804 |
1804 |
|
|
25*11 |
38*11 |
27*11 |
|
|
|
Die Buchstaben der inneren drei Spalten haben jeweils eine durch 11 teilbare ZS+FS, die ZS+FS der äußeren Buchstabenspalten ergänzen sich durch 428+386 = 814 zu 74*11 und Umkehrungzahl des mittleren Ergebnisses. Die ungeraden Spalten bilden die Punkte, die geraden die Linien des Kreisdurchmessers. Das durch 11 teilbare 3:2 Spaltenverhältnis ist demnach 112:52 = 4*(28:13) = 4*41. Die Linien der Verhältniszahl 13 übernehmen im DR-Kreuz aus 41 Elementen die Punkte.
Beachtenswert sind die FW der ZS und FS:
|
1 |
2 |
3 |
4 |
5 |
sm |
FW |
|
239 |
56 |
30 |
163 |
74 |
562 |
283 |
|
16 |
33 |
30 |
69 |
173 |
321 |
110 |
|
255 |
89 |
60 |
212 |
247 |
883 |
393 |
Die FW der vier Summen betragen 1804+393 = 2197 = 13*13*13. 3*13 ist auf die Elemente dreier hexagonaler Doppeldreiecke und auf die Punkte dreier DR-Kreuze beziehbar:
|
|
6. Die ZS+FS der Dreifachzählung des unten stehenden linken 1x1 Modells beträgt 305+257 = 562 = 2*281 >283:
Wie die obere Hexagongrafik zeigt, entsprechen den Einzelziffern der ZS+FS 562 die Elemente eines hexagonalen Doppeldreiecks. Die Addition von 562+283 = 845 = 5*13*13 >31 führt von 13 zur Umkehrsumme 31.
Erstellt: Mai 2018
