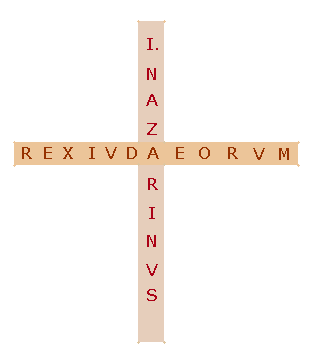zurück

weiter

Gematrische Untersuchung der beiden lateinischen Kreuzesinschriften

III. Das Prinzip der Zwei

IV. Die Verknüpfung der Zahlenwerte

V. 2-stellige Kreiszahlen und 3-stellige Rückkehrzahlen

VI. Beziehung der beiden Zahlenwerte durch Aufgliederung

III. Das Prinzip der Zwei

Die gematrische Verbindung der beiden Kreuzinschriften ging von der stillschweigenden Annahme aus, daß sie nach göttlicher Vorsehung einander zugeordnet sind, also zusammen eine Sinneinheit bilden. Beide sind in sich selbst stimmig, bedürfen einander also nicht unbedingt als Ergänzung. Wenn sie aber zusammengehören, eröffnen sie konsequenterweise neue Sinnaspekte, indem das Ganze in besonderer Weise ins Blickfeld rückt.

Inhaltliche Parallelstrukturen sind ein bedeutendes Prinzip biblischer Poesie, besonders in den Psalmen. Parallelismus membrorum – Parallelismus der Glieder ist der Fachausdruck dafür. Ein Gedanke wird in zwei Halbversen zweimal ausgedrückt, entweder auf ähnliche, oder gegensätzliche Weise, z.B.:

Jesaja 1,3: "Ein Rind kennt seinen Besitzer und ein Esel die Krippe seines Herrn."

Psalm 1,6:"Der Herr kennt den Weg der Gerechten, aber der Gottlosen Weg vergeht."

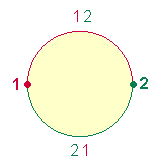
Das dahinter stehende Prinzip ist offensichtlich das der Teilung eines Ganzen in zwei Hälften. Es ist das Ursprungsprinzip jeder weiteren Differenzierung. Teilt man eine Kreislinie in zwei Hälften, wiederholt die zweite Hälfte spiegelbildlich die erste:

Die beiden Kreisbogenhälften haben nun durch ihre zwei Begrenzungspunkte eine gemeinsame Mitte. Darin ist gleichzeitig ein trinitarisches Prinzip verwirklicht: Die beiden göttlichen Personen werden durch die dritte miteinander verbunden:

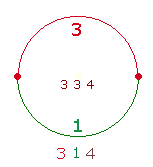
Eine Kreisbogenhälfte ist durch eine Linie und zwei Begrenzungspunkte definiert. Für die zweite Hälfte bleibt nur noch ein Element übrig Das Verhältnis ist dann 3:1. Dasselbe gilt auch umgekehrt von der unteren Kreisbogenhälfte. Auch kann sich eine Hälfte durch die andere definieren lassen. Dann ist das Verhältnis jeweils 1:3. Diesen Grundverhältnissen steht die Ganzheit von 4 Elementen gegenüber. Die Zusammensetzung der Ziffern 3 1 4 gibt bezeichnenderweise die ersten 3 Zahlen des Kreisfaktors p wieder. Wird jeder Hälfte die Definition 3 zuerkannt, erhält man mit 3+3+4 bereits die Summe 10 des Dezimalsystems. Tatsächlich führt der Faktorenwert (FW) von 334 = 2*167 = 169 = 13*13 wieder zum genannten Grundverhältnis zurück.

Von diesen Zusammenhängen aus ist es nicht weit bis zu der Überlegung, daß jeder Gedanke ein synonymes Spiegelbild hat. Indem der Sprecher dieses sucht, vergewissert er sich des gemeinsamen Dritten. Ebenso wird erst durch Aufzeigen eines Gegensatzes das Ganze im Gleichgewicht gehalten. Die Fähigkeit zur Unterscheidung von Gegensätzen ist eine Grundbedingung für freiheitliches Handeln.

Möglicherweise liegen diesem auffälligen Stilmittel des Parallelismus Modelle des Kreises und des Dezimalsystems zugrunde. Wenn es im alten Israel ein diesbezügliches mathematisches Denksystem gegeben hat, könnte seine Weitergabe mit der Zerstörung Jerusalems außerordentlich gelitten haben.

Vielleicht hat es einen tieferen Grund, daß der Davidstern, der sich ab dem 15. Jahrhundert zunehmend zu einem Symbol jüdischer Identität entwickelte, identisch mit dem Tetraktysstern ist, der die wesentlichen Modelle des Dezimalsystems enthält. Die beiden einander gegenüber liegenden Dreiecke erfüllen darin am auffälligsten das Prinzip der Zweiheit in der Ganzheit.

IV. Die Verknüpfung der Zahlenwerte

1. Die Zahlenwerte (ZW) der beiden Kreuzesinschriften, 326 und 269, zeigen bereits in der Zahlenfolge 26 und der Zusammengehörigkeit von 3 und 9 verwandte Züge. Sie sind beziehbar auf das Hexagon, auf die beiden Tetraktys und auf die drei Doppelrauten (DR).

Ich kann hier nur auf einige wenige Zahlenbedeutungen eingehen.

2. Die Zahlen 3+2 und 6 (=3+3) im ZW 326 geben den Doppelaspekt von Durchmesser- und Radialelementen wieder. Die Primfaktoren 2*163 weisen auf 2 Tetraktys mit ihrer Aufteilung von je 10 Punkten hin.

Aus 26 Elementen besteht ein Oktaeder, der sich aus 2 DR zusammensetzt. Wenn sich jede der 3 DR mit jeder verbindet, ergeben sich 3 Oktaeder.

Die Zahl 36 weist auf je 18 Rahmenelemente zweier Tetraktys hin. Der 18. Buchstabe ist das S, das im Namen IESUS zweimal vorkommt und sich auf seine Doppelnatur von Gott und Mensch beziehen könnte.

3. Der ZW 269 ist zerlegbar in 26, 69 und 29. Die Zahl 69 = 3*23 bezeichnet besonders die 3 numerierten Achsen des Hexagon, 26 ist der FW von 69.

Die Aufteilung (3+3)+9 = 6+9 zeigt der DR-Rahmen: 6 Elemente gehören dem äußeren Kreisring, 9 dem hexagonalen Teil der DR an.

Die Zahl 29 bezeichnet besonders das DR-Kreuz mit 29 Elementen des Rahmens.

4. Eine weitere Erhellung beider ZW ergibt sich aus der ZW/FW-Verrechnung:

	ZW	FW	Sm.	FW	Sm.
	326	165
	269	269
Sm.	595	434	1029	24
FW	29	40	69	26
Sm.			1098	50
FW			69	12	81

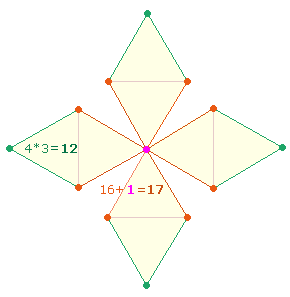
Die Faktoren der Zahl 595 sind 5*7*17 = 12+17 = 29. Diese Aufteilung ist beziehbar auf 12 Außen- und 17 Innenelemente des DR-Kreuzes:

Die den Zahlen 12 und 17 entsprechenden Buchstaben sind M R und verweisen auf MARIA, die Mutter Jesu, die Jesu Erlösungsaufgabe bis unters Kreuz mitgetragen hat.

Die Faktoren der Zahl 1029 sind 3*7*7*7. Sie weisen auf 3*21 Elemente der 3 DR hin. Die Schreibung 3*7³ gibt die 13 Punkte des Tetraktyssterns wieder.

Die FW 24+26 bilden das Verhältnis 2*(12+13). Das Hexagon und seine Erweiterung bestehen jeweils aus 12+13 Elementen, wenn auch dem äußeren Kreis ein Mittelpunkt zugestanden wird. Das dadurch wiedergegebene Flächenverhältnis ist 1:3.

Die Zahl 81 schließlich bezeichnet in ihren Einzelziffern 8 symmetrische Durchmesserelemente und den Mittelpunkt des Tetraktyssterns. In der Darstellung 3⁴ hat sie trinitarische Bedeutung.

V. 2-stellige Kreiszahlen und 3-stellige Rückkehrzahlen

1. Sobald man einen Punkt auf einer Kreislinie festlegt, kann dieser als Anfang und Ende einer Kreisbewegung angesehen weden. Ein weiterer Schritt ist die Kreislinienteilung durch einen zweiten Punkt. Wenn man beide Punkte numeriert und die Kreislinie zu einer geraden Strecke ausdehnt, tritt ein dritter Punkt hinzu, der die Ausgangszahl erhält. Zusammengesetzt ergibt sich daraus eine dreistellige Zahl, ihre Urgestalt ist 121 = 11*11:

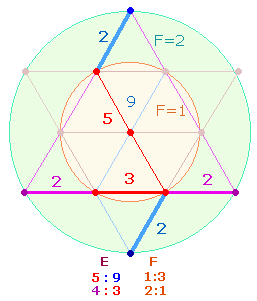
2. Nun sind die addierten ZW 595 (326+269) und FW 434 (165+269) der beiden Inschriften solche dreistellige Rückkehrzahlen. Man kann sie sich also auf zweistellige Kreiszahlen 59 und 43 zurückgesetzt vorstellen. Ihre Einzelziffern beziehen sich auf die Elemente (E) der Hexagon- und der DR-Achse sowie der Tetraktysseite und sind auf ihre trinitarischen Flächengrößen (F) umzusetzen:

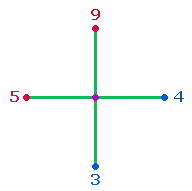
3. Die Einzelziffern können den äußeren Enden eines Achsenkreuzes zugeordnet werden:

Die Zahlen wurden kreisförmig angeordnet, da, wie sich später zeigen wird, ein Zahlenverhältnis gegen den Urzeigersinn zustande kommt, nämlich 49:53.

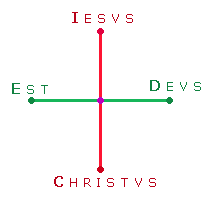
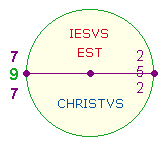
Wenn man die Zahlen der vertikalen und horizontalen Achse in Buchstaben umsetzt, erhält man IC und ED. Man kann diese Buchstaben als Initialen ansehen und sie zu der Aussage erweitern:

Die Wahrscheinlichkeit dieser Deutung erhält dadurch Überzeugungskraft, daß die Zahlensummen + Faktorensummen (ZS+FS) der beiden Achsen sich wie 2:1 verhalten:

	ZS	FS	Sm.		ZS	FS
IESUS	70	36		EST	42	32
CHRISTUS	112	76		DEUS	47	26
Sm.	182	112	294		89	58	147
294:147 = 7*21*(2:1) = 21²

Wie die Namen IESUS CHRISTUS hat auch EST den durchschnittlichen ZW 14 je Buchstabe. Dies ermöglicht die weitere Gleichung IESUS EST CHRISTUS. Die FS sind jeweils durch 4 teilbar: 4*(9+8+19) = 4*36 = 16*9. Die 16 Buchstaben der Gleichung haben also auch einen durchschnittlichen FW, sodaß der durchschnittliche Gesamtwert 23 beträgt.

Die 2*8 Buchstaben lassen sich auf die Rahmenlinien eines DR-Kreuzes eintragen. Ich möchte hier jedoch auf zwei Kreishälften zurückkommen. Nach Einziehung einer Kreisachse aus 5 Elementen besteht jede Kreishälfte (Bogen, Fläche, Achse) aus 2+5 = 7 Elementen, der ganze Kreis jedoch aus 9 Elementen. Auf diese Weise kommt die Summe (7+7)+9 = 23 zustande. Das Prinzip der Teilung besagt also auch, daß eine inhaltliche oder mathematische Gleichung eine Ganzheit bildet:

Daß das Ganze etwas anderes ist als zwei Hälften, zeigt sich darin, daß die Teilbarkeit durch 16 erst nach der Addition der beiden FS 68+76 möglich ist.

Die gematrische Gleichung IESUS EST CHRISTUS könnte bedeuten: Jesus ist (tatsächlich) der (verheißene) Messias. Gematrie erweist sich so als providentielles Verifikationsinstrument.

Erstellt: Dezember 2007

index