Die fehlenden stabilen Elemente 43 und 61
Zweimal
drei Stufen
I. Einleitung
III. Ineinanderfügung
I. Einleitung
1. Die Zahlen 43 und 61 bewirken nicht nur eine Dreiteilung der Zahlen von 1-83, sondern führen auch zu einer dreifachen Stufung, wenn die drei Zahlenreihen konzentrisch betrachtet werden. Denn die 17 Zahlen von 44-60 enden nach 8 Paaren und der Mittelpunktszahl 52, die 22 Zahlen von 62-83 nach 11 Paaren, und es bleiben noch 10 Paare der Zahlen 1-42 übrig.
2. Vorbild für die Dreistufung ist insbesondere die Tetraktys:
|
|
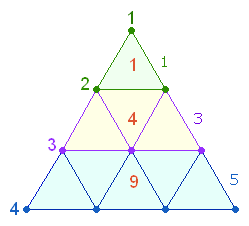
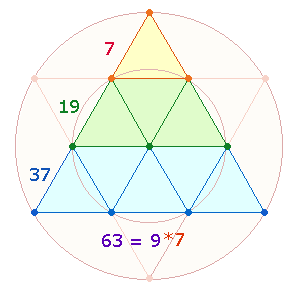
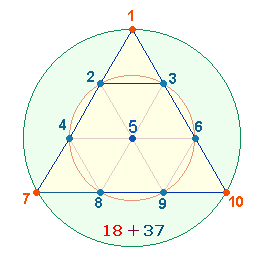
Mit vier Punkteebenen gehen drei Dreiecksebenen einher. Wenn die Dreiecke je fortschreitendem Rahmendreieck aufaddiert werden, ergibt sich die Zahl 1+4+9 = 14 gegenüber 9 realen Dreiecken. Berücksichtigt man Punkte, Linien und Dreiecke, beträgt die Aufaddierung 7+19+37 = 63:
|
|
Das Ergebnis ist insofern bemerkenswert, als die 7 Elemente des Dreiecks allen 9 Dreiecken zukommen.
Wenn die Meßzahl 7 für jedes Dreieck gilt, gibt es für jede der vier verschiedene Figuren des Hexagramms eine Diskrepanz zwischen der Zahl der Dreieck mal 7 und der tatsächlichen Zahl der Elemente. Das Hexagramm z.B. besteht aus 49 Elementen und enthält 12 Dreiecke, die einzeln gerechnet zusammen 84 Elemente ergeben. Der Differenzbetrag ist 35, sodaß von 12*7 Elementen 5*7 eingespart werden. Das Gesamtergebnis der vier Figuren ist:
|
|
Elemente |
3-Ecke |
mal 7 |
|
Hexagon |
25 |
6 |
42 |
|
Hexagramm |
49 |
12 |
84 |
|
2 Tetraktys |
74 |
18 |
126 |
|
3 Doppelrauten |
63 |
12 |
84 |
|
|
211 |
48 |
336 |
|
336-211 = 125 = 5³ |
|||
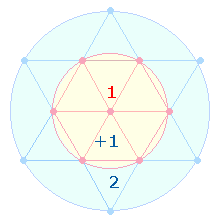
Den 7 Einzelfiguren entspricht die durchschnittliche Zahl von 48 Elementen. Die Gesamtzahl der 211 Elemente scheint wesentlich der Tatsache zu dienen, daß das Verhältnis des äußeren Hexagrammkreises zum hexagonalen Kreis (2+1):1 beträgt:
|
|
3. Die im ersten Teil durchgeführte Analyse der Stufen 2 und 1 ist auf alle drei Ebenen auszudehnen, bevor eine Berechnung der Ineinanderfügungen angegangen werden kann.
1. Die ZS+FS, von der Mitte und von den Rändern aus berechnet, sind:
|
St.3 |
Mitte |
Rand |
|
|
|
||||
|
|
ZS |
FS |
sm |
ZS |
FS |
sm |
SM |
SM |
GS |
|
|
2576 |
1164 |
3740 |
2576 |
1129 |
3705 |
5152 |
2293 |
7445 |
|
FW |
38 |
104 |
142 |
38 |
1129 |
1167 |
76 |
1233 |
1309 |
|
8754 = 3*2918; 1309
= 7*11*17 |
8754 |
||||||||
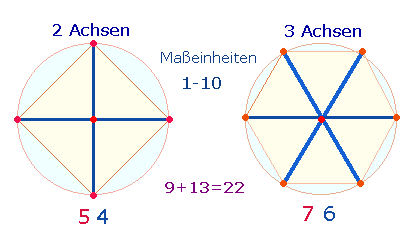
Die Einzelziffern der Zahl 2918 stellen 2+9 Punkte dar, die 1+8 Maßeinheiten begrenzen. Die FW-Summe 1309 bezieht sich auf die beiden Achsenkreuze, die 10 Maßeinheiten enthalten:
|
|
2. Die Werte der zweiten und ersten Stufe, die im ersten Teil ermittelt wurden, führen mit denen der dritten Stufe zu folgenden Ergebnissen:
|
St. |
2+1 |
3 |
sm |
|
ZS |
1612 |
5152 |
6764 |
|
FS |
975 |
2293 |
3268 |
|
FW-S |
619 |
1309 |
1928 |
|
|
3206 |
8754 |
11960 |
|
11960 = 40*13*23 >FW 47 |
|||
Die FW-S 619 ist der FW der Zahl 1234 und somit für das Dezimalsystem konstitutiv. Der FW 47 ist mit den beiden oben dargestellten Achsen in Verbindung zu bringen. Denn wenn man man jede der 5 Achsen, von denen jede aus 5 Elementen besteht, mit 5 multipliziert, erhält man durch Addition von 22+25 die Summe 47. Die beiden Teilsummen lassen sich durch das Produkt 260*46 bilden. Aber auch die Aufteilung 24+23 ist sinnvoll.
Die Zahlen 13 und 23 sind auf die Radialelemente und Durchmesserelemente des Hexagramms mit seinen beiden konzentrischen Kreisen zu beziehen. Sie geben beide 7 Flächeneinheiten wieder. Die Radialelemente der zweiten Radialhälfte werden durch 40 durch das Produkt 5*8 repräsentiert, das als 5+8 zu interpretieren ist.
3. Die gesamte FW-S 1928 stellt das Kreismodell des Dezimalsystems dar, das bereits im ersten Teil erklärt wurde.
Die Zahlenpaare 19 und 28 mit Umkehrmöglichkeit sind sowohl in der Tetraktys als auch in der Doppelraute zu finden. In Anknüpfung an oben Dargelegtes betragen die 10 Punkte, unnumeriert auf drei Ebenen aufaddiert, 3+6+10 = 19 und numeriert 6+21+55 = 82. Bei zwei Tetraktys sind beide Summierungen zu verdoppeln.
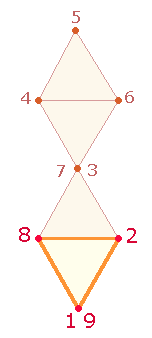
Numeriert man die 7 Punkte der Doppelraute schleifenförmig, setzen sich die Einzelziffern der unteren beiden Ebenen zu 19 und 82 zusammen:
|
|
4. Da die Zahlen 1 und 3 für die Ebenen 2 und 1 eine zentrale Rolle spielten, stellt sich die Frage, ob die Produktzahl 13 eine verbindende Rolle in den 3 Ebenen spielt. Tatsächlich erweist sich 13 als gemeinsamer Faktor der ZS+FW-S und FS+FW-S:
|
St. |
3 |
2 |
1 |
sm |
|
ZS |
2576 |
376 |
430 |
3382 |
|
FW |
38 |
53 |
50 |
141 |
|
141 = 3*47; 3523 = 13*271 |
3523 |
|||
Die Summe 3523 ist auf 7046 und 13*542 zu verdoppeln.
|
St. |
3 |
2 |
1 |
sm |
|
FS Mi. |
1164 |
231 |
239 |
1634 |
|
FW |
104 |
21 |
239 |
364 |
|
364 = 13*28 |
1998 |
|||
|
1998 = 54*37 |
||||
|
St. |
3 |
2 |
1 |
sm |
|
FS Ra. |
1129 |
237 |
268 |
1634 |
|
FW |
1129 |
82 |
71 |
1282 |
|
2916 = 54*54 |
2916 |
|||
Beide Summen sind durch 54 teilbar, das Zahlenverhältnis beträgt 54*(37:54) = 54*91 = 378*13. Das FS:ZS-Verhältnis ist demnach 13*(378:542) = 13*920 = 40*13*23. Die interne Differenz beträgt 164 = 4*41.
Die Zahl 54, als 2*27 zu verstehen, bezieht sich auf 25+2 Elemente des Hexagons und 24+3 seiner Erweiterung. Ein Zusatzelement ist der Kreisbogen und die Kreisfläche. Bei der Erweiterung ist der Mittelpunkt zu wiederholen, um den zweiten konzentrischen Kreis zu bilden.
Die Zahl 378 ist die Summe der Zahlen 1-27. Das Produkt 14*27 ist aufgeteilt zu denken in 7+7 und 13+(7+7). Die Einzelziffern beziehen sich auf die Punkte des Hexagons, der Erweiterung und des ganzen Hexagramms. Die Aufteilung gibt 1+3 und 3+4 Flächeneinheiten der beiden konzentrischen Kreise wieder.
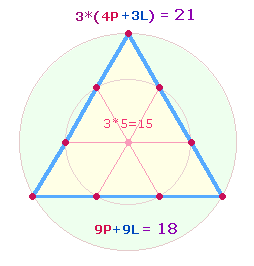
Die Aufteilung der Zahl 378 in 18*21 kann in Bezug zum Tetraktysrahmen gesehen werden, dessen Elemente entweder insgesamt oder je einzelner Seite gezählt werden können, entweder als 9 Punkte + 9 Linien oder als dreimal 4 Punkte + 3 Linien:
|
|
1. Den zwei Tetraktys entsprechend sind zwei Ineinanderfügungen zu ermitteln, konzentrisch von der Mitte und von den Ränder aus. ZS und FS werden getrennt bestimmt:
|
|
ZS |
Mitte |
FS |
|
|
||||
|
St. |
1 |
2 |
3 |
sm |
1 |
2 |
3 |
sm |
GS |
|
1 |
430 |
– |
– |
430 |
239 |
– |
– |
239 |
669 |
|
1+2 |
430 |
376 |
– |
806 |
239 |
231 |
– |
470 |
1276 |
|
1+2+3 |
430 |
376 |
2576 |
3382 |
239 |
231 |
1164 |
1634 |
5016 |
|
|
1290 |
752 |
2576 |
4618 |
717 |
462 |
1164 |
2343 |
6961 |
|
4618 = 2*2309; 2343 = 3*11*71 |
|||||||||
|
|
ZS |
Rand |
FS |
|
|
||||
|
St. |
1 |
2 |
3 |
sm |
1 |
2 |
3 |
sm |
GS |
|
1 |
430 |
– |
– |
430 |
268 |
– |
– |
268 |
698 |
|
1+2 |
430 |
376 |
– |
806 |
268 |
237 |
– |
505 |
1311 |
|
1+2+3 |
430 |
376 |
2576 |
3382 |
268 |
237 |
1129 |
1634 |
5016 |
|
|
1290 |
752 |
2576 |
4618 |
804 |
474 |
1129 |
2407 |
7025 |
|
2407 = 61*79; 7025 =
281*25 > FW 291 |
|||||||||
Die ZS beider Zählungen sind gleich, die Differenz der Gesamt-FS beträgt 64 und ebenso der Gesamt-ZS+FS.
2. Die Faktoren der beiden Gesamtergebnisse 6961+7025 = 13986 sind 378*37 = FW 18+37 = 55. Die Zahl 378 wurde oben erklärt. 37 ist die Zahl der Tetraktyselemente. Die Addition 18+37 ist in der numerierten Tetraktys anzutreffen, wenn die drei Eckpunkte und die sieben hexagonalen Punkte getrennt gezählt werden:
|
|
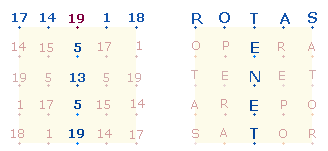
3. Die Primzahl 6961 ist bemerkenswert, da 69 und 61 zwei zentrale ZS des SATOR-Quadrats sind:
|
|
Die Mitte der T-Form bildet der Buchstabe T mit dem ZW 19 selbst, und alle drei Zahlenwerte sind im FW 619 der Zahl 1234 enthalten.
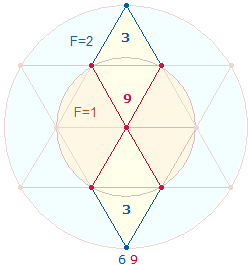
Die Einzelziffern der Summen 6961 und 7025 sind in der Doppelraute (DR) präsent. Es geht dabei stets um ihre Aussage hinsichtlich der beiden Kreisflächenverhältnisse 2:1 und 3:1. Der DR-Rahmen besteht aus 15 Elementen, 3+3 davon gehören dem Erweiterungsring an, 9 dem hexagonalen Bereich:
|
|
Die 3+3 Punkte der DR erfassen beide konzentrischen Kreise als Ganzheit und vertreten daher die Flächengröße 3, während der Mittelpunkt nur dem hexagonalen Bereich zuzuordnen ist und daher 1 Flächeneinheit bezeichnet.
Die Einzelziffern der zweiten Gesamt-Summe 7025 beziehen sich ebenfalls auf die DR. Dabei geben die Ziffern 7 und 2+5 die Flächengröße 3 und 2+1 wieder. Beide Gesamtsummen 6961 und 7025 vertreten demnach 7+6 = 13 Flächeneinheiten.
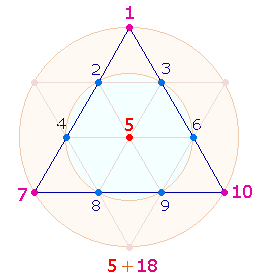
4. Die FW der beiden Gesamtsummen sind 6961+291 = 7252 = 2*2*7*7*37 = FW 55. Sowohl der Faktor 37 als auch der FW 55 weisen auf eine zweite numerierte Tetraktys hin. Das FS:ZS-Verhältnis ist 14*37* (14:27) = 518*41. Die Aufteilung 5+18 fügt zu der Numerierungssumme 18 der drei Eckpunkte noch die Zahl 5 des Mittelpunktes hinzu:
|
|
Erstellt: August 2014