26 Primzahlen im Oktaeder
I. Einleitung
1. Zum Sinngefüge der Zahlen gehört die Wiederholung grundlegender Zahlenbedeutungen: Was etwa im Kreis und im Hexagon grundgelegt ist, kommt auch in der hexagonalen Erweiterung des Hexagramms mit seinen zwei Tetraktys und drei Doppelrauten (DR) zum Vorschein.
2. Aus einem Doppelrautenkreuz läßt sich ein Oktaeder bilden. Bei diesem Vorgang werden die äußeren Punkte zu jeweils einem verbunden, wodurch sich die Zahl von 9 Durchmesserelementen der Doppelraute, die dreifach links, rechts und in der Mitte zu zählen sind, auf je 8 verkürzt.
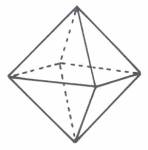
3. Der Oktaeder stellt das Endziel des Kreises und seiner dreiachsig-hexagonalen Entfaltung dar:
|
|
|
Wie die linke Kreisfigur ist auch der Oktaeder spiegelbildlich als zusammengesetzt aus zwei gegenüberstehenden Pyramiden zu denken. Die Besetzung der Oktaederelemente mit 26 Primzahlen wird zeigen, wie sich die Zahlenverhältnisse zweier Kreishälften wiederholen.
II. Anordnung auf 26
Elementen des Oktaeders
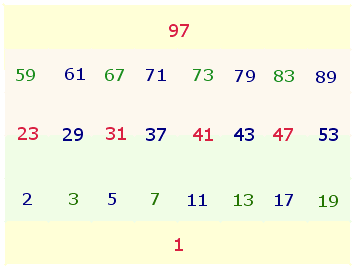
1. Entsprechend dem Aufbau des Oktaeders lassen sich die 26 Primzahlen von 1-100 von unten nach oben anordnen:
|
|
|
Die 6 Ecken sind rot, die 12 Kanten blau und die 8 Flächen grün gekennzeichnet. Als Fortsetzung der Zahl 1 ist hier eine Kante gewählt, auch eine Fläche ist möglich. Die Summe der 26 Primzahlen ist die Primzahl 1061. In zweistelliger Aufteilung ist ein DR-Kreuz vorstellbar aus 6+1 Punkten (61) und 7+1 Punkten (10+61 = 71).
Die Summen der 6+12+8 Zahlen sind:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FW |
|
E. |
1 |
23 |
31 |
41 |
47 |
97 |
|
|
|
|
|
|
240 |
16 |
|
K. |
2 |
5 |
11 |
17 |
29 |
37 |
43 |
53 |
61 |
71 |
79 |
89 |
497 |
78 |
|
F. |
3 |
7 |
13 |
19 |
59 |
67 |
73 |
83 |
|
|
|
|
324 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1061 |
110 |
|
497 = 71*7; 240:324 = 12*(20:27) = 564; 32+78 = 110 |
||||||||||||||
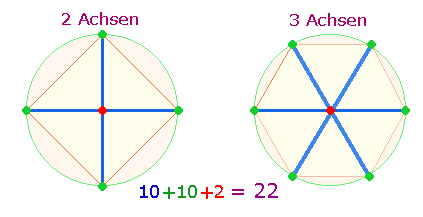
Die Einzelziffern des Produkts 71*7 geben die 15 Rahmenelemente der DR wieder. Die Verhältniszahlen 20:27 sind auf den Doppelaspekt von zwei Figuren aus zwei und drei Achsen beziehbar, die 10 Maßeinheiten grundlegen:
|
|
Zählt man für jede Achse einen Mittelpunkt, sind es 15 statt 12 Punkte:
|
ME |
10 |
10 |
20 |
|
Pu. |
12 |
15 |
27 |
|
|
22 |
25 |
47 |
Daß Ecken und Flächen gegenüber den Kanten eine Einheit bilden, zeigen die gleichen FW 16 und die FW-Addition 32+78: die Einzelziffern der beiden zweistelligen Zahlen ergänzen sich zu jeweils 10: 3+7, 2+8.
Für das Volumen steht die 27. Primzahl 101 zur Verfügung. Fügt man sie zu den Summen der Ecken und Flächen, erhält man 564+101 = 665 = 7*95. Es ergibt sich so das Verhältnis 497:665 = 7*(71:95) = 7*166 = 1162.
2. Befriedigende Zahlenverhältnisse ergeben sich, wenn man die 8*3 Zahlen addiert und sie zweimal konzentrisch einander zuordnet:
|
o. |
|
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
679 |
7*97 |
104 |
|
|
Mi. |
|
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
|
304 |
16*19 |
27 |
|
|
u. |
1 |
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
|
78 |
6*13 |
18 |
|
|
|
|
84 |
93 |
103 |
115 |
125 |
135 |
147 |
161 |
963 |
1061 |
|
149 |
1210 |
|
84+161
= 245; 103+135 = 238; 245:238 = 7*(35:34)
= 7*69 = 483 |
||||||||||||||
|
93+147 = 240; 115+125 = 240; 240+240 = 480; 483:480 = 3*(161:160) >
3+30+3+15 = 45+6 = 33+18 =51 |
||||||||||||||
Die oberste Summe setzt sich zusammen aus 8+1 Zahlen und 97*(6:1).
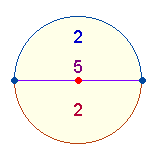
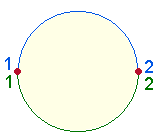
3. Die FS 149 und Gesamtsumme 1210 führt bereits zur Betrachtung der oben erwähnten Verhältnissen zweier Kreishälften. Die Einzelziffern der Palindromzahl 121 = 11*11 können zwei numerierte Teilungspunkte der Kreislinie darstellen:
|
|
|
Die zwei Kreisbogenhälften können durch 121 oder 12 und 21 wiedergegeben werden. Die zweite Kreisbogenhälfte kehrt spiegelbildlich zum Ausgangspunkt zurück. In der rechten Figur besteht jede Kreishälfte aus 2+5 Elementen: einer Kreislinien- und Flächenhälfte und dem Durchmesser. Zählt man die Durchmesserelemente zweimal, kommen 7+7 Elemente zustande, zählt man sie nur einmal, sind es 7+2 Elemente. Die Addition beider Aspekte ergibt 14+9 = 23. In dieser Weise ist hier die FS 149 zu verstehen. Die Einzelziffern stellen außerdem Quadrate der Zahlen 1 2 3 dar.
Logisch sinnvoll ergibt das Produkt 12*21 die in der rechten Figur untereinander geschriebenen Elemente als dreistellige Zahl 252.
Erstellt:
August 2014
Bearbeitet:
Juni 2019