Faktorenwerte von 11-100
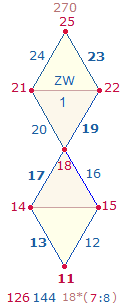
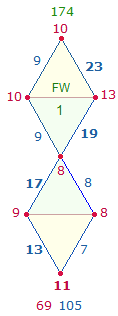
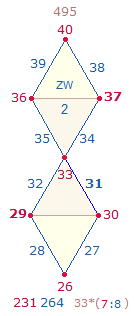
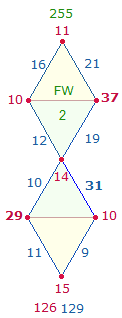
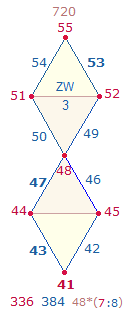
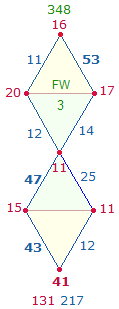
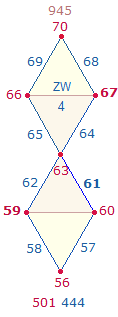
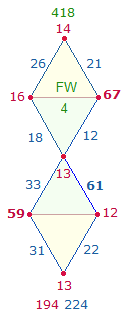
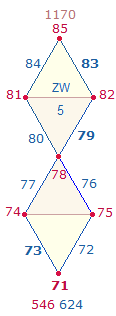
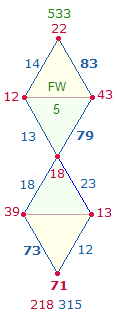
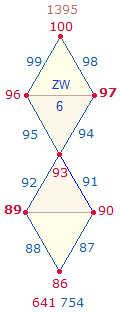
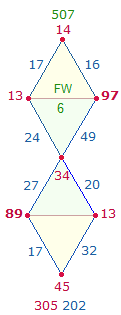
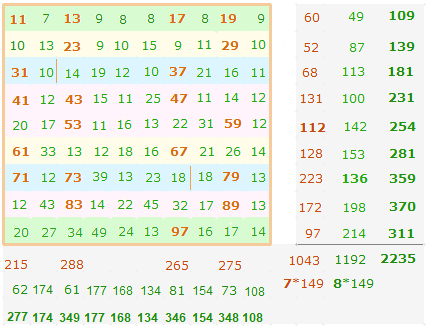
1. Die Zahlen 11-100 enthalten 21 Primzahlen und 69 zusammengesetzte Zahlen. Primzahlen haben gleiche Faktorenwerte (FW). Die Faktorensumme (FS) der 21 Primzahlen beträgt 1043 = 7*149, die Faktorensumme der 69 zusammengesetzten Zahlen 8*149. Als geometrisches Modell für 7 und 8 eignen sich die 7 Punkte und 8 Linien des Rahmens der Doppelraute (DR). Wenn man die FW der 90 Zahlen in 6*15 aufteilt und auf den Rahmenelementen von 6 DR einträgt, ist das überraschende Ergebnis, daß die FS der 7 Punkte 7*149 und die der 8 Linien 8*149 beträgt. Die ZW und FW werden nachfolgend dokumentiert, Primzahlen sind fettgedruckt:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Grafiken sind die ZW und FW der 6 DR auf je eine DR übertragen:
|
|
|
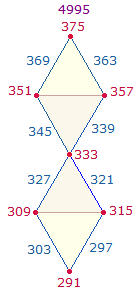
2. Die ZS schreiten um 6 Zähler je Gruppe voran. Die Gesamtsumme beträgt 45*111 = 15*333 = 4995. Die ZS von 6*2 spiegelsymmetrischen Paaren betragen jeweils 666, die ZS von zweimal je 2*3 "Dachelementen" 1998, die ZS der drei Schnittpunkte 999. Da die Dachelemente eine eigene Bedeutung besitzen, ist die Aufteilung in 12+3 Elemente sinnvoll: Die FS der 12 Dachelemente ist 1854 = 18*103 = FW 111, die ZS+FS 3996+1854 = 5850 = 45*130 = FW 31. Die FS der drei Schnittpunkte beträgt 381 = 3*127 = FW 130, die ZS+FS 999+381 = 1380 = 3*460 = 60*23. Für die 12 DR bedeutet dies eine durchschnittliche ZS+FS 115. Die beiden FS ergeben die FW 111+130 = 241, was dem Hauptfaktor der Gesamtsumme 7230 = 30*241 (s.u.) entspricht, die beiden ZS 3996 und 999 ergeben die FW 50+46 = 96, zusammen 337. Die Einzelziffern der Primzahl 337 geben die Punktestruktur des Tetraktyssterns wieder:
|
|
Die ZS+FS des unteren und oberen DR-Punktes betragen 666+283 = 949 = 73*13. Zu den Dachelementen hinzugerechnet, ergibt sich so 13*(450+73) = 13*523 = 6799. Übrig bleibt die ZS+FS 431 des Mittelpunktes.
Wie die ZS 4995 ist auch FS 2235 durch 15 teilbar. Das FS:ZS-Verhältnis ist daher 15*(149:333), der Differenzbetrag 15*184 = 120*23.
3. Die FS der Gruppen 2 3 6 und 1 4 5 ergeben jeweils Teilbarkeit durch 15 und konstitutive Verhältniszahlen: 255+348+507 = 1110; 174+418+533 = 1125; 1110:1125 = 15*(74:75), die ZS+FS derselben Gruppen Teilbarkeit durch 30:
|
|
2 |
3 |
6 |
sm |
1 |
4 |
5 |
sm |
GS |
|
FS |
255 |
348 |
507 |
1110 |
174 |
418 |
533 |
1125 |
2235 |
|
ZS |
495 |
720 |
1395 |
2610 |
270 |
945 |
1170 |
2385 |
4995 |
|
|
750 |
1068 |
1902 |
3720
|
444 |
1363 |
1703 |
3510 |
7230
|
|
3720:3510 = 30*(124:117)
= 30*241 |
|||||||||
|
124 = 4*31; 117
= 9*13; 533:1170 =
13*(41:90) = 13*131 |
|||||||||
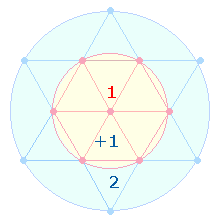
Den Einzelziffern der Umkehrfaktoren 31 und 13 liegt das Kreisflächenverhältnis 3:1 bzw. 1:3 der beiden konzentrischen Kreise des Tetraktyssterns zugrunde. Sie weisen auf das Urbild der Zahlen, den einen Gott in drei Personen hin:
|
|
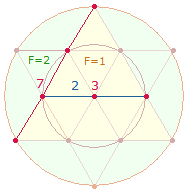
Die Einzelziffern der Gesamtsumme 7230 sind auf 7 Elemente einer Tetraktysseite und 2 Radialmaße und 3 Punkte einer Hexagonachse beziehbar, sie geben das Kreisflächenverhältnis 3:1 wieder:
|
|
Eine weitere Deutung folgt im Anschluß.
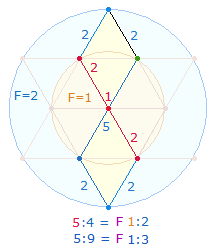
4. Die Einzelziffern von 149 verweisen auf 1+4 hexagonale Durchmesserelemente und 9 Elemente der DR-Zickzacklinie. 5:9 Durchmesserelementen entspricht so das trinitarische Flächenverhältnis 1:3 der beiden konzentrischen Kreise:
|
|
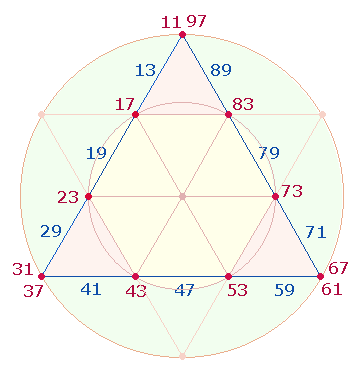
5. Von den 90 Zahlen zwischen 11-100 sind 21 Primzahlen und 69 zusammengesetzte Zahlen, die das Verhältnis 3*(7:23) bilden. Die 21 Primzahlen kann man auf je 4 Punkte und 3 Linien der drei Tetraktysseiten eintragen:
|
|
Es zeigt sich, daß entsprechend den 3 Linien und 4 Punkten je Tetraktysseite die Summe der Linien- und Punktezahlen 3*149 und 4*149 beträgt.
21 und 69 kann man auch zweistellig zu 2169 zusammensetzen, was durch 3 geteilt zu 723 führt. Die Faktoren der Umkehrung 6921 sind 9*769, die FW beider Zusammensetzungen 247+775 = 1022 = 14*73. Es ist an 2*7 Punkte des Tetraktyssterns und 7+3 Punkte der Tetraktys zu denken.
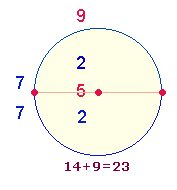
Nun kann 149 auch als 14+9 = (5+9)+(5+4) = 23 gelesen werden. Den beiden Klammerausdrücken entsprechen die Kreisflächenverhältnisse 1:3 und 1:2, und ergeben so zusammen 7 Flächeneinheiten. 9 ist FW von 14, zusammengesetzt aus 7+7. Der 7. Punkt des Erweiterungsbereichs ist für eine äußere Kreisbogenziehung erforderlich, damit das Kreisflächenverhältnis 3:1 ermöglicht wird.
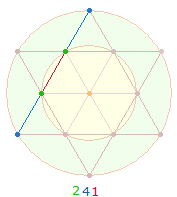
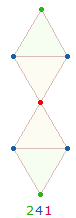
Die ZS+FS 7230 = 30*241 kann so in Verbindung zur Zahl 149 gebracht werden. 30*241 läßt sich aufteilen in 2*(24+1)*15. Zweimal 24+1 ist auf 25 hexagonale und 25 Erweiterungselemente des Tetraktyssterns, 15 auf die Rahmenelemente der DR beziehbar. Als Einzelziffern gibt 241 das Muster einer Tetraktysseite und der DR-Punkte ab:
|
|
|
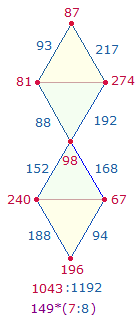
6. Die FS der zweimal zwei hexagonal gekreuzten Linien halten numerisch das Gleichgewicht zu den vier äußeren:
|
|
Alle vier Summen der hexagonalen Linien sind durch 8 teilbar und ergänzen sich reihum durch 8+2 zu jeweils 10, wodurch die 2 Querlinien mit eingebunden werden:
|
88 |
192 |
280 |
|
152 |
168 |
320 |
|
240 |
360 |
600 |
|
240:360 = 120*(2:3) |
||
|
280:320 = 40*(7:8) |
||
Die inneren und äußeren Linien halten das numerische Gleichgewicht durch angrenzende Verhältniszahlen: 600:592 = 8*(75:74) und bilden mit der Restsumme das Verhältnis 600:1635 = 15*(40:109).
7. Für die ZS und FS der 21 Primzahlen sowie der 69 zusammengesetzten Zahlen ergeben sich folgender FW:
|
PZ |
sm |
ZZ |
sm |
SM |
SM |
GS |
||
|
ZS |
FS |
|
ZS |
FS |
|
|
|
|
|
1043 |
1043 |
2086 |
3952 |
1192 |
5144 |
4995 |
2235 |
7320 |
|
156 |
156 |
312 |
40 |
155 |
195 |
|
507 |
|
|
312:195 =
3*13*(8:5) = 3*13² |
||||||||
|
3952 = 16*13*19; 3952+195 = 4147 = 11*13*29 >53 |
||||||||
1. Die ursprüngliche Anordnung der 90 ZW und FW in Doppelrautenkreuzen befindet sich nun an anderer Stelle.
2. Die Ordnung in den 9*10 Zahleneinheiten soll anhand der folgenden Grafik untersucht werden:
|
|
In fortlaufender Addition ergibt sich für die Primzahlen Teilbarkeit durch 7 nach der 6. und 12. Primzahl 29 und 53, bzw. nach der 9. und 15. von der obersten Zahl 97 aus gezählt: 112:931 = 7*(16:133); 364:679 = 7*(52:97). Teilbarkeit durch 8 ist der Mitte von 1192 am nächsten nach der Zahl 63, der 39. zusammengesetzten Zahl: 536:856 = 8*(67:82).
Teilbarkeit
durch 15 für addierte FS der Primzahlen und zusammengesetzten Zahlen
lassen sich horizontal in 9 Zehnereinheiten und
vertikal in 10 9-er Reihen nach Einerstellen
untersuchen. Die Zusammengehörigkeit der horizontalen
Reihen ist durch farbliche Unterlegung kenntlich gemacht. Zu nennen sind
zunächst die zwei konzentrisch-komplementären
Reihen 1+9 und 3+7. Ihre Summen sind 420+540 = 960 = 64*15. Eine zweite Summe 420 = 28*15 kommt durch 139+281 der Reihen 2
und 6 zustande. Übrig bleiben die Reihen 4+5+8 mit der Summe 855
= 57*15 = 45*19. Der benachbarte Faktor 56 ergibt sich aus 2*420
= 840 = 56*15. Übrig bleibt 540 = 36*15.
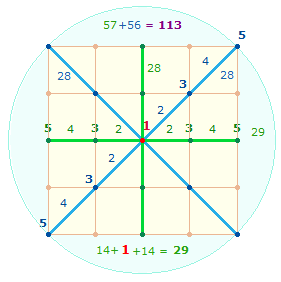
Die Addition 57+56 = 113 weist auf ein Quadrat hin, dessen
8 Achsenarme vom Mittelpunkt aus von 1-5
numeriert sind:
|
|
Es bleibt der Faktor 36
übrig, der als 4*9 Achsenelemente
interpretierbar ist, so daß ein solchermaßen zweifaches Quadrat zusammen aus 1+4 = 5 Mittelpunkten
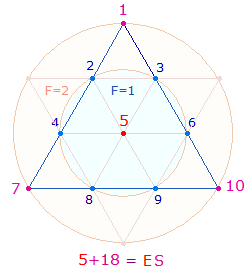
und je Achsenarm aus der Summe 14+4 = 18 besteht. 5+18
entspricht gematrisch lateinisches ES – Du bist mit hoher theologischer Bedeutung, da
beide Summanden in der numerierten Tetraktys vorzufinden sind:
|
|
Den 1+3 Punkten entspricht das Kreisflächenverhältnis 1:2, deutet
also sowohl auf den einen Gott in drei Personen als auch den 1+2 Personen selbst.
Die horizontalen Reihen der Primzahlen und der zusammengesetzten
Faktoren weisen zwei Besonderheiten auf: Erstens,
sie enthalten mit 112 und 136 je eine Zahl, die durch 7 bzw. 8 – wie
ihre Gesamtsummen – teilbar sind. Zweitens,
dieselben Zahlen wiederholen sich durch die FS
der ersten beiden Reihen: 60+52 = 112 und 49+87 = 136.
Das Verhältnis der beiden Zahlen 112:136 = 8*(14:17) = 8*31 weist in seinen Verhältniszahlen auf die 7 Punkte des Hexagons und 10
Punkte der Tetraktys hin sowie auf ihre FW 7+7 = 14.
Aus 7 Punkten besteht auch die Erweiterung
des Tetraktysstern, wenn zur Ziehung eines äußeren Kreisbogens der hexagonale
Mittelpunkt ein zweites Mal verwendet wird. Durch diesen zusätzlichen Punkt
wird das Kreisflächenverhältnis 3:1 des
äußeren Kreises zum inneren bewirkt. 8*31 ist
als 5:3 Radialelemente der DR-Zickzacklinie zu verstehen, die das
Kreisflächenverhältnis 3:1 wiedergeben.
Der Doppelung der Radialelemente entsprechen zweimalige FS 112 und 136.
Die Summen der vertikalen Reihen zeigen reizvolle Beziehungen:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
277 |
174 |
349 |
177 |
168 |
134 |
346 |
154 |
348 |
108 |
|
|
|
|
345 |
480 |
|
|
|
||
|
|
|
|
345:480 = 15*(23:32) |
|
|
|
|||
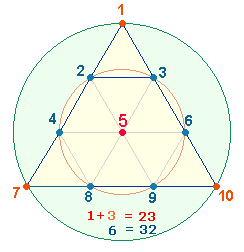
Die vier konzentrischen Innenglieder sind paarweise durch 15 teilbar und ergeben die Umkehrfaktoren 23:32, die als Summe der Zahlen 1-10 in einer numerierten Tetraktys dargestellt werden können:
|
|
Die zwei linken Summen sind durch 3 teilbar, die zwei rechten nicht. Ebenso sind von den zweimal drei Außengliedern drei durch 3 teilbar und drei nicht, und zwar so, daß sich jeweils eine andersartige Zahl zu zwei gleichartigen gesellt. Wenn die nicht durch 3 teilbaren Summen der Außenglieder zu den durch 3 teilbaren Innengliedern hinzugefügt werden, und dies ebenso umgekehrt geschieht, ergibt sich das angrenzende Verhältnis (780+345): (480+630) = 1125:1110 = 15*(75:74).
Die Summen der vier Primzahlreihen sind konzentrisch – von außen nach innen – durch 7 teilbar: 215+275 = 490; 288+265 = 553; 490:553 = 7*(70:79).
Dasselbe Verhältnis – mit Umstellung der Verhältniszahlen – ist auch bei den FS der zusammengesetzten Zahlen zu finden:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
62 |
174 |
61 |
177 |
168 |
134 |
81 |
154 |
73 |
108 |
|
297 |
560 |
335 |
|||||||
Die sechs konzentrischen Außenglieder bilden mit den vier Innengliedern das Verhältnis 632:560 = 8*(79:70).
3. Die Zahlenordnung ist auf Symmetrie und Komplementarität angelegt, wie es dem Wesen des Kreises entspricht. Die FW haben als Summen zwar ihre eigenen Ordnungen, aber sie sind andererseits untrennbar mit ihren ZW verbunden. Dies zeigt sich eindrucksvoll an den Zahlen von 11-100, wenn man ihre ZW und FW in zwei komplementären Reihen addiert, z.B. 11+11 = 22; 100+14 = 114; 111+25 = 136. Die beiden Reihen kommen nach 22 Paaren zur Hälfte der 90 Zahlen mit den ZW 33 und 78. Um genau zu zwei Hälften von je 45 Zahlen zu gelangen, muß 33 oder 78 für die erste Hälfte ausgewählt werden. Es sind 78+18, die für ein ideales Zahlenverhältnis sorgen. Die in 10-er Einheiten angegebenen FS können in obiger Grafik nachgeprüft werden. Jedes komplimentäre Paar hat die ZS 111:
|
|
ZS |
sm |
FS |
sm |
GS |
||
|
|
2*20 Z |
5 Z |
|
2*20 Z |
5 Z |
|
|
|
1.H. |
2220 |
300 |
2520 |
929 |
151 |
1080 |
3600 |
|
|
30 Z |
15 Z |
|
30 Z |
15 Z |
|
|
|
2.H. |
1665 |
810 |
2475 |
766 |
389 |
1155 |
3630 |
|
|
3885 |
1110 |
4995 |
1695 |
540 |
2235 |
7320 |
|
3600:3630 = 30*(120:121); |
|||||||
|
2475:2520 =
45*(55:56) ;1080:1555 = 15*(72:77) |
|||||||
|
1080:2520 = 360*(3:7); 1155:2475 = 165*(7:15) |
|||||||
Die
beiden Gesamt-ZS+FS 3600
und 3630 bilden angrenzenden
Konstitutivzahlen 120:121.
Ermöglicht wird dies durch die Differenz 75 der beiden FS 1080 und 1155,
sodaß die um 45 kleinere ZS schließlich um 30 höher liegt als
die ZS+FS der ersten Hälfte. Die Einzelziffern der
Verhältniszahlen 72:77 gibt zwei
Aspekte von Elementen zweier Kreishälften wieder:
|
|
Eine Kreishälfte besteht aus 7 Elementen: aus 5 Durchmesserelementen, einer halben Kreislinie und halben Kreisfläche. Es bleiben weitere 2 Elemente für die zweite Kreishälfte. Es können jedoch auch für jede Kreishälfte 7 Elemente gezählt werden. Auf diese Weise läßt sich die Zahl 149 aus 14+9 Elementen zweier Kreishälften zusammensetzen.
Das Verhältnis 72:77 kommt außerdem nach 5 konzentrischen PZ-Paaren zustande: 83+421 = 504:539 = 7*(72:77), das Umkehrverhältnis nach 18 konzentrischen Faktorenpaaren der zusg. Zahlen: 616:576 = 77:72. Die Addition der vier Verhältniszahlen führt zu 1120:1115 = 5*(224:223) = 5*447.
Das ermittelte ZS+FS-Verhältnis 3600:3630 kam aus (22+23)+(23+22) Zahlen zustande. Den Einzelziffern entsprechen 4 Erweiterungselemente der DR-Zickzacklinie und 5 hexagonale Durchmesserelemente:
|
|
Bei
fortlaufender Addition der ZS+FS
gelangt man nach 47 Zahlen, d.h.
einschließlich 57, zu 2410, einem Drittel der ZS+FS-Gesamtsumme.
Eine Wiederholung dieser Summe ist nur unter Weglassung des letzten FW möglich. Die folgende Tabelle dokumentiert die
dreimal 2410 ZS+FS:
|
|
11-57 |
58-80/81 |
81/82-100 |
|
|||
|
Anzahl |
47 |
47 |
24 |
23 |
19 |
20 |
180 |
|
|
ZS |
FS |
ZS |
FS |
ZS |
FS |
|
|
|
1598 |
812 |
1668 |
742 |
1729 |
681 |
7230 |
|
812:742 = 14*(58:53) = 14*111 |
|||||||
4. 13 konzentrische Paare zusammengesetzter Faktoren (von außen nach innen) ergeben 126:321 = 3*(42:107) = 3*149 = 447. 26:43 zus.gesetzten Faktoren entspricht also (etwa) das Verhältnis (3:5)*149. Der Grund könnte darin liegen, daß 3:5 Radialelemente einer DR-Zickzacklinie das Kreisflächenverhältnis 1:3 wiedergeben. Die Einzelziffern weisen in einzigartiger Weise auf die 15 Rahmenelemente hin durch 2*4 Linien und 7 Punkte.
Nach 5 PZ-Paaren und 17 Paaren zusg. Faktoren ergibt sich Teilung durch 15: 504+591 = 1195:1140 = 15*(73:76). 44 und 46 sind die Konstitutivzahlen für 90.
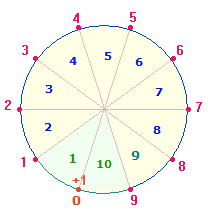
5. Warum sind die 90 Zahlen von 11-100 so bedeutsam? Aus zwei Gründen: Erstens, die Multiplikation 9*10 entspricht 9 Durchmesserelementen und 2*5 Radialelementen der DR-Zickzacklinie im Tetraktysstern. Zweitens, sie setzen auf zweistelliger Ebene die Grundzahlen von 1-9 fort. Diesseits und jenseits von 1 und 9 ist die 0 als Begrenzungspunkt Beginn und Ende von 10 Maßeinheiten, wie sich auf einer Kreislinie erkennen läßt:
|
|
|
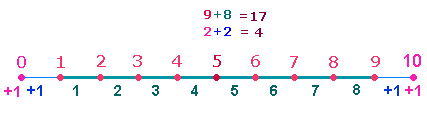
In der Streckendarstellung sind 11 Begrenzungspunkte für 10 Maßeinheiten erforderlich. Dieses Erfordernis erfüllt die DR mit 10 Maßeinheiten; den 7 Punkten sind noch die 4 Dreiecksflächen zuzufügen. Die FS der Zahlen 1-10 und 101-110 sind:
|
|
PZ |
zsgZ |
|
|
1-10 |
18 |
28 |
46 |
|
101-110 |
420 |
142 |
562 |
|
|
438 |
170 |
608 |
|
11-100 |
1043 |
1192 |
2235 |
|
|
1481 |
1362 |
2843 |
Die Gesamtsumme 2843 ist eine Primzahl, die 2+8 Linien und 4+3 Punkte der DR wiedergibt. Den Einzelziffern der PZ-Summe 1481 – ebenfalls eine Primzahl – entsprechen 1+4 Durchmesserelemente des Hexagons und 8+1 der DR-Zickzacklinie in der Bedeutung von 1:3 Kreisflächeneinheiten.
Schließlich ist auch noch an die nächste Zahl 111 zu denken, die die drei göttlichen Personen darstellt. Die Faktoren der FS 2883 = 3*31*31 = FW 65. Die Faktoren weisen auf den einen Gott in drei Personen hin.
Erstellt: Januar 2021