Prime
Number 1
|
|
1. A prime number,
according to worldwide consensus, is a number greater than 1 that is divisible only by itself and by 1. That excludes 1 as
a prime number. But truth does not depend on human decisions: Whether 1 IS prime or not,
is a logical and an ontological problem. In fact, according to Wikipedia-information 1 could be found in lists of prime numbers until
1956. It is to be considered whether the current definition of prime numbers
has the right logic on its side.
2. The reason generally
forwarded for the exclusion of number 1 from
the class of prime numbers is that the factors of composite numbers would not
be written unequivocally as 2*3 for example,
but also as 1(n)*2*3.
So what happens is
that in order to make the definition of prime numbers as simple as possible,
number 1 must quit the field. In fact,
according to the prevailing definitions, there aren't just two, but three groups of numbers: "composite,
prime, and the unit 1". This makes things
complicated again.
3. What seems necessary
is a CHANGE OF PERSPECTIVE: the priority of
definition should not lie with the prime numbers,
but the composite numbers. A composite
number is to be understood as a particular positions in a multiplication
series, starting with number 1: Any individual
number is to be defined as an individual, for example, 5
and it's 1*5. If it is doubled and trebled, it's 2*5 = 10 and 3*5 = 15. The
first factor of the multiplication series is called MULTIPLIER,
the second MULTIPLICAND. So 10 would be the second successive result in
multiplying 5. The multiplicator 1 is IMMANENT to
the initial multiplicand number and so need not be placed in front of it.
The basic number 1 itself can be multiplier
as well as multiplicand. As a multiplier it
occurs only once, and a multiplicand it is a constant in successive groups of
ones: 1*1, 2*1, 3*1. As to number 1 the application of both multiplier and multiplicand
constitutes a SQUARE 1*1, and equal progression of multipliers and multiplicands
creates more squares: 2*2, 3*3 etc.
4. Composite numbers and
prime numbers consequently should be defined as follows:
A composite number
consists of two or more factors greater than 1
within an imaginal series of multiplication,
for example 3*5 from preceding 2*5 or 3*4. Its
result 15 can start another series of
multiplication with multiplicands greater than 1.
A prime number does not contain two
or more factors greater than 1. It is the
beginning of a multiplication series (1)*PN, 2*PN etc.
As the current definition of prime numbers is
inadequate, it has to be reformulated. The order should be composite numbers first and prime numbers second:
|
|
The new definition eliminates the
aspect of division as unessential.
5.
For mathematicians numbers are a matter of axiomatic theory, i.e., they
do not concern themselves with the origins of numbers and their possible
meanings and structures. So it eludes their attention that the decimal system
contains innumerable well-ordered proportions and relationships. What could be
the sense of two classes of numbers if there didn't exist a wise system of
order. One example is the composite numbers (CN)
and prime numbers (PN) of 1-13 in subsequent additions:
|
CN |
|
|
|
4 |
|
6 |
|
8 |
9 |
10 |
|
12 |
|
49 |
|
PN |
1 |
2 |
3 |
|
5 |
|
7 |
|
|
|
11 |
|
13 |
42 |
|
49:42 = 7*(7:6) |
||||||||||||||
6:7 numbers bring about an inversive
relation of 7:6.
Without 1 no relation would be possible.
Furthermore, every NUMERIC
VALUE (NV) is matched by a FACTORAL VALUE
(FV). The relationship of the two values can be written as an equation: 6 = 2*3: NV = 6, FV = 2+3 = 5;
5 = (1)*5: NV = 5, FV = 5; 1 = (1)*1: NV = 1, FV = 1. Numerical
values and fact oral values of prime numbers
are identic. As to the numbers 1-13 the
following relations emerge:
|
|
CN |
sm |
PN |
sm |
GS |
|||||||||||
|
NV |
4 |
6 |
8 |
9 |
10 |
12 |
49 |
1 |
2 |
3 |
5 |
7 |
11 |
13 |
42 |
91 |
|
FV |
4 |
5 |
6 |
6 |
7 |
7 |
35 |
1 |
2 |
3 |
5 |
7 |
11 |
13 |
42 |
77 |
|
|
48 |
36 |
84 |
36 |
48 |
84 |
168 |
|||||||||
|
35:42 = 7*(5:6); 77:91 = 7*(11:13) |
||||||||||||||||
The numeric sums (NS) + factoral sums (FS) of the 6 CN
and 7 PN are
equally 84. The NS+FS of the first
9 (4-9, 1-7) and the last 4 (10-13) numbers are 84 (48+36;
36+48) again.
The total of numbers within the decimal system proves
to be a network of innumerable relations, which would seriously be impaired without 1 understood as prime number.
6.
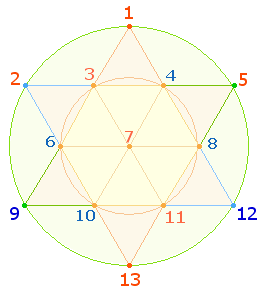
On an ontological level the FIRST of
all numbers is the origin of everything being. Among geometrical figures the CIRCLE symbolises eternity most clearly. It can be
subdivided by three axes and completed into a hexagon
and furthermore EXTENDED into a hexagram containing two TETRACTYS.
A tetractys is an equilateral triangle consisting of 1+2+3+4
points, well-known from the Greek mathematician Pythagoras. The entire figure
of hexagram consists of 13 points:
|
|
The 13 numbers are placed from left to right and top
to bottom. The inner and outer
circle are in ratio 1:3.
There are composite numbers (blue) and prime
numbers (orange) both on the 6 extension
points and the 7 hexagonal points. It has to
be examined what ORDER there exists between
the two classes of numbers.
To begin
with, the regular numeration results in a regular ratio 6:7 of the two sums 42 and 49 correspondent to the 6
numbers in the extension area and 7 in the
hexagonal areas. The composite and prime numbers in both areas are divisible by
7:
|
|
extension |
sm |
hexagonal |
sm |
tot. |
||||||
|
cn |
9 |
12 |
|
|
21 |
4 |
6 |
8 |
10 |
28 |
49 |
|
pn |
1 |
2 |
5 |
13 |
21 |
3 |
7 |
11 |
|
21 |
42 |
|
|
|
|
|
|
42 |
|
|
|
|
49 |
91 |
The table
is arranged according to composite numbers (cn) and prime numbers (pn). The two
sums form the ratio 42:49, which can be written as 7*(6:7).
The sum 42 of the 6
extension numbers is the same as the 7 prime
numbers between 1 and 13, and vice versa the 7 hexagonal numbers agree with the sum 49 of the 6
composite numbers.
written:
September 2018