Primzahl 1
1. Eine Primzahl ist nach geltender Definition größer als 1 und nur durch sich selbst und durch 1 teilbar. Als Grund für den Ausschluß der 1 aus der Klasse der Primzahlen wird insbesondere fehlende Eindeutigkeit hinsichtlich der zusammengesetzten Zahlen angeführt, z.B. 6 könne dann sowohl als 2*3 als auch als 1(n)*2*3 dargestellt werden.
Der Zahl 1 wird also um einer Regelvereinfachung willen die Eigenschaft einer Primzahl abgesprochen. Die Mathematiker verlagern damit aber nur das Problem. Es entsteht nämlich die unbefriedigende Situation, daß alle Zahlen nun in drei Gruppen einzuteilen sind, in zusammengesetzte Zahlen, in Primzahlen und die singuläre Zahl 1. Eine einheitliche Sicht aller Zahlen ist damit nicht zu erreichen.
Laut dem englischsprachigen Wikipedia-Eintrag wurden bis 1956 Primzahllisten veröffentlicht, die mit 1 begannen. Heute aber wird die Zahl 1 im Internet so häufig und hartnäckig als Primzahl abgelehnt, daß man meinen könnte, die Autoren wollten ihre eigenen Zweifel bekämpfen.
2. Es stellt sich daher die Frage, ob die bisherige Definition überhaupt der logisch richtige Weg ist, wenn also die Zahlen von oben nach unten statt von unten nach oben definiert werden und der Definition der Primzahlen der Vorzug vor der Definition der zusammengesetzten Zahlen gegeben wird. Der natürliche Definitionsweg ist eher von den zusammengesetzten Zahlen aus zu gehen, so daß ihre Faktoren nicht als Teiler, sondern als multiplikative Bestandteile anzusehen sind. Denn Teilung setzt vorherige Multiplikation voraus.
Demnach sollte man zusammengesetzte Zahlen, wie bereits angedeutet, als multiplikative Reihen verstehen, die jeweils mit 1 als Multiplikator beginnen. Eine beliebige Ausgangszahl, die als einmal und erstmals vorkommend vorzustellen ist, kann sich verdoppeln und verdreifachen usw., so daß die Reihe entsteht (1*)5 = 5, 2*5 = 10, 3*5 = 15 usw. Die Zahl 10 bildet so die zweite Stelle des Multiplikanden 5. Die Zahl 1 ist der zu multiplizierenden Ausgangszahl immanent und muß ihr nicht als Multiplikator vorangestellt werden.
Die Zahl 1 selbst kann als Multiplikator und als Multiplikand auftreten. Der Multiplikator sei die Ausgangsmultiplikation aller fortlaufenden Zahlen, die durch den Multiplikanden bezeichnet werde, also 1*1, 1*2, 1*3 ..., 1*99 usw. In ihrem ersten Auftreten kann die Zahl 1 sie selbst sein oder im Zusammenwirken von Multiplikator und Multiplikand ein QUADRAT bilden, das durch gleichmäßiges Fortschreiten von Multiplikator und Multiplikand zu weiteren Quadraten führt: 2*2, 3*3 usw.
Zusammengesetzte Zahlen und Primzahlen sind demnach folgendermaßen zu beschreiben:
Eine zusammengesetzte Zahl bezeichnet die Position einer Multiplikationsreihe aus zwei oder mehr Faktoren größer 1 und ist gleichzeitig Ausgangspunkt einer weiteren Multiplikationsreihe. Eine Primzahl dagegen ist nur Ausgangszahl einer Multiplikationsreihe, also (1*)PZ.
Die zwei erforderlichen Definitionsformeln sollten folgendermaßen lauten:
|
|
Die neue Definition macht den Teilungsaspekt der geltenden entbehrlich. Die bisherige Definition widerstrebt dem gesunden Menschenverstand und erscheint als eine künstliche, realitätsferne Festlegung.
3. Noch einleuchtender ist die Umkehr der Rollen durch 1*1, 1*2, 1*3 usw., wenn man von zwei Aspekten der Zahlen ausgeht: Unter dem ersten Aspekt bilden die Zahlen ein apriorisches Beziehungs- und Bedeutungsgefüge, dessen Sinn in sich selbst besteht. Es sind die Zahlen an sich.
Unter dem zweiten Aspekt sind diese Zahlen an sich Zählmittel sowohl für apriorische Formstrukturen, z.B. von 8 Flächen des Würfels als auch für alles sonstige Zählbare.
Gleiches und Unterschiedenes kann addiert werden: Die Addition von 5 Äpfeln und 8 Nüssen ergibt 13, 7 Tugenden und 7 Laster 14.
Jede Zählbarkeit beginnt mit 1. Vom Standpunkt her, daß Einzelnes nicht für sich allein steht, sondern zu einer Art bzw. einem Oberbegriff gehört, ist Zusammengehöriges mit 1 gleichzusetzen. Es ergibt sich so für den Beginn eines jeden Zählvorganges 1*1 Art/Zusammengehöriges. Das erstmalige Auftreten von Zusammengehörigem erhöht sich zählenderweise jeweils um 1 und ist dann so darstellbar: (1+1)*1, (1+1+1)*1 usw. 5 Äpfel + 8 Nüsse sind so 5*Art 1 + 8*Art 2 = 13*1 Eßbares.
Auf diese Weise beginnt jede Zählung mit 1*1, und so kann 1 durch sich selbst und durch 1 geteilt werden, wenn man bei der herkömmlichen Definition unbedingt bleiben will.
4. Mathematiker beschäftigen sich nicht mit Ordnungen von Zahlen und mit proportionalen Verhältnissen von Zahlensummen. Eine organische Sichtweise des Zahlensystems ist ihnen fremd. Dennoch besteht dieses in vielfältigen Beziehungsgefügen. Welchen Sinn hätten die beiden Klassen von Zahlen, wenn zwischen ihnen nicht eine weise Ordnung bestünde? Es sollen hierfür zwei Beispiele linearer Zahlenfolge angeführt werden:
·
Zusammengesetzte Zahlen (ZZ)
und Primzahlen (PZ) können ein Zahlenverhältnis
bilden, wie z.B. die Zahlen 1-13:
|
ZZ |
|
|
|
4 |
|
6 |
|
8 |
9 |
10 |
|
12 |
|
49 |
|
PZ |
1 |
2 |
3 |
|
5 |
|
7 |
|
|
|
11 |
|
13 |
42 |
|
49:42 = 7*(7:6) |
||||||||||||||
6:7 Zahlen bilden das Umkehrverhältnis 7:6. Kein Verhältnis wäre möglich ohne Zuordnung der 1 zu den Primzahlen.
·
Wie zusammengesetzte Zahlen und Primzahlen so
können auch deren Faktoren addiert werden.
Die Beziehung von Zahlenwert (ZW) und Faktorenwert (FW)
läßt sich als Gleichung darstellen: 6 = 2*3: ZW = 6, FW = 2+3 = 5; 5 = (1)*5: ZW = 5, FW = 5; 1 = (1)*1: ZW = 1, FW = 1. ZW und FW von
Primzahlen sind also identisch. Im Falle der Zahlen 1-13
ergeben sich folgende Zahlenverhältnisse:
|
|
ZZ |
sm |
PZ |
sm |
GS |
|||||||||||
|
ZW |
4 |
6 |
8 |
9 |
10 |
12 |
49 |
1 |
2 |
3 |
5 |
7 |
11 |
13 |
42 |
91 |
|
FW |
4 |
5 |
6 |
6 |
7 |
7 |
35 |
1 |
2 |
3 |
5 |
7 |
11 |
13 |
42 |
77 |
|
|
48 |
36 |
84 |
36 |
48 |
84 |
168 |
|||||||||
|
35:42 = 7*(5:6); 77:91 = 7*(11:13) |
||||||||||||||||
Die ZS+FS der ZZ und PZ sind jeweils 84, ebenso die ZS+FS der ersten 9 und der letzten 4 Zahlen.
Unzählige weitere
proportionale Beziehungen zwischen FS und ZS können ermittelt werden, wenn 1 als
Primzahl verstanden wird.
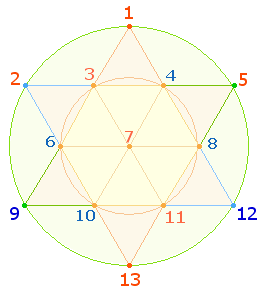
5. Auf ontologischer Ebene ist die Zahl 1 Ursprung alles Seins. Unter den geometrischen Figuren symbolisiert der Kreis am sinnfälligsten die Unendlichkeit, aus der vor Milliarden von Jahren die Endlichkeit hervorging. Der Kreis läßt sich weiter zum Hexagon und dieses zum Tetraktysstern entwickeln. Die Tetraktys ist ein Zahlendreieck aus 1+2+3+4 Punkten, das bei dem Mathematiker Pythagoras eine zentrale Rolle einnimmt. Die ganze Figur umfaßt zwei Tetraktys und besteht aus 13 Punkten:
|
|
Die 13 Zahlen sind
von oben nach unten der Reihe nach auf den Punkten eingetragen. Das Flächenverhältnis des inneren zum äußeren Kreis beträgt 1:3. Zusammengesetzte (blau) und Primzahlen (rot)
befinden sich sowohl auf den 7 hexagonalen
als auch auf den 6 Erweiterungspunkten. Zu
untersuchen ist, welche ORDNUNG zwischen den
beiden Bereichen herrscht:
Zunächst bedingt die fortlaufende Numerierung
der spiegelsymmetrischen Punkte von außen nach innen das ZS-Verhältnis 42:49 =
7*(6:7) entsprechend der Anzahl der Punkte. Es
zeigt sich, daß die ZS der zusammengesetzten
und der Primzahlen jeweils durch 7 teilbar
sind:
|
|
außen |
sm |
innen |
sm |
GS |
||||||
|
ZZ |
9 |
12 |
|
|
21 |
4 |
6 |
8 |
10 |
28 |
49 |
|
PZ |
1 |
2 |
5 |
13 |
21 |
3 |
7 |
11 |
|
21 |
42 |
|
|
|
|
|
|
42 |
|
|
|
|
49 |
91 |
Die 6
äußeren Zahlen übernehmen also die ZS der 7 Primzahlen und die 7 hexagonalen Zahlen die ZS
der 6 zusammengesetzten Zahlen. Die ZS+FS sind:
|
|
außen |
innen |
|
||||
|
|
ZZ |
PZ |
sm |
ZZ |
PZ |
sm |
GS |
|
ZS |
21 |
21 |
42 |
28 |
21 |
49 |
91 |
|
FS |
13 |
21 |
34 |
22 |
21 |
43 |
77 |
|
|
34 |
42 |
76 |
50 |
42 |
92 |
168 |
|
76:92 = 4*(19:23) |
|||||||
6. Die gefunden Summen sind nun auf die beiden Tetraktys anwendbar, dabei gelten die hexagonalen Summen für beide Tetraktys, während 2*3 Eckpunkte jeweils einer zuzuordnen sind:
|
|
Tetraktys 1 |
Tetraktys 2 |
|
||||
|
|
au. |
in. |
sm |
au. |
in. |
sm |
GS |
|
ZZ |
21 |
28 |
49 |
0 |
28 |
28 |
77 |
|
PZ |
1 |
21 |
22 |
20 |
21 |
41 |
63 |
|
sm |
22 |
49 |
71 |
20 |
49 |
69 |
140 |
|
77:63 = 7*(11:9) |
|||||||
Erstellt: September 2018