Entwicklung des Dezimalsystems
IX. Strecken-und Kreismodell
B. Vier
Doppelzählungen im Tetraktysstern
Wie die Dezimalstrecke von 0-10 durch die Zusammenführung
beider Enden zu einem Kreis um einen Begrenzungspunkt verringert wird, so läßt
sich eine Abfolge von Begrenzungspunkten und Maßeinheiten in einer
geschlossenen geometrischen Figur als eine Strecke denken, die einen
Begrenzungspunkt mehr benötigt.
Im
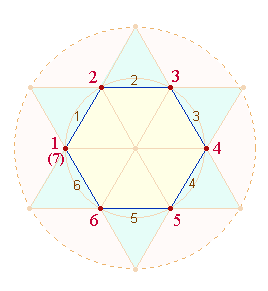
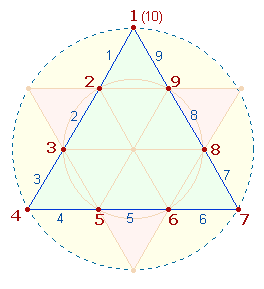
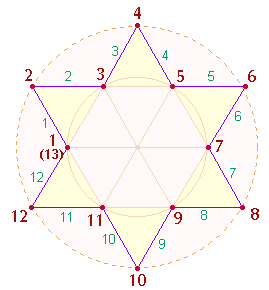
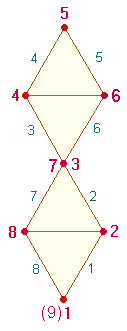
Tetraktysstern gibt es vier geschlossene Abfolgen von Punkten und Linien: die
Umgrenzung des Hexagons, den Tetraktysrahmen, die Doppelraute und den Umriß des
Tetraktyssterns. Sie enthalten 6, 9, 8 und 12 Maßeinheiten, zusammen 35. Beachtet
man, daß es 2 Tetraktys (9) und 3 Doppelrauten (8) gibt, entspricht das Verhältnis (6+9):(8+12) = 15:20 = 5*(3:4) der
Häufigkeit des jeweiligen Zahlenpaares. Durch die Addition von 1*9+2*8 = 25
erhält man 35+25 = 60 Maßeinheiten im Verhältnis 5*(7:5).
Im Streckenformat kommen zu den 60 Punkten noch 7 Punkte
hinzu, so daß das Streckenformat 67 Punkte + 60 Maßeinheiten = 127 Elemente enthält.
|
|
|
|
|
|
C. Die Streckenelemente 19 und 21
Die vier
Numerierungen ermöglichen zahlreiche sinnvolle Berechnungen. Eine davon
erscheint mir besonders bedeutsam und soll ausführlicher dargestellt werden:
1. Wenn man die
Numerierungen der Punkte (P) und der Maßeinheiten (ME) addiert, erhält man für
die Zahlen 6,8,9,12 jeweils die Werte 21+36+45+78 = 180*2 = 360. Der
Durchschnittswert der vier Numerierungen beträgt 180/4 = 45, das entspricht der Addition der Zahlen 1 bis 9. Die 4 Numerierungen
weisen daher das trinitarische Verhältnis 3:1 auf.
2. Im
Streckenformat kommt zur jeweils letzten Zahl noch ein Begrenzungspunkt (BP)
hinzu: 7+9+10+13 = 39. Der Gesamtwert für die BP beträgt demnach
180+39 = 219.
Die Zahl 219 weist bereits auf die Elemente 21 und (1)9 hin. Die Teilungsfaktoren
sind 3*73. Die Einerzahlen 3, 7, 3 geben die Punkteverteilung der Tetraktys und
des Tetraktyssterns wieder: 3 Eckpunkte der Tetraktys, 7 Hexagonpunkte und drei
Eckpunkte für die zweite Tetraktys. Da sich die beiden Tetraktys
gegenüberstehen, lassen sich die 3 Zahlen im Umkehrformat darstellen 37/(7)3.
Zwei weitere Umkehrzahlen ergeben sich aus dem Faktorenwert (FW) von 219 =
3+73 = 76. Die FW von 76 und der Umkehrzahl 67 sind 23+67 = 90. Das Produkt 9*10 führt wieder zur Zahl 19 und die FW
von 9 und 10, 6+7 = 13, zur Anzahl der Punkte des
Dezimalsterns zurück.
Die Zahlen 6 und 7 sind in zweifacher Hinsicht bedeutsam für die beiden
Tetraktysrahmen:
Eine Seite
des Tetraktysrahmens besteht aus 4P+3L = 7 Elementen, der gesamte Rahmen aus
3*7 = 21 Elementen, beide Rahmen aus 6*7 = 42
Elementen. Die Zählung jeder Rahmenseite bewirkt, daß die Eckpunkte dopelt
gerechnet werden. Je Tetraktysrahmen ergibt sich dadurch das Verhältnis 21:18
bzw. 18:21, d.h. 3*(7:6) bzw. 3*(6:7).
3. Durch die
Addition der ME- + BP-Werte erhält man 180+219 = 399. Die Zahl 399 wiederholt in ihrer Produktaufteilun 21*19 die Bestandteile
von 219. Man erkennt aus den Einerzahlen 3,9,9 leicht die 9 Punkte und 9 Linien
des Tetraktysrahmens und die zusätzlichen 3 Eckpunkte.
Möglich, aber schwieriger ist die Zuordnung zu 2
Doppelrauten (DR), die zur Bildung eines Oktaeders führen. Zwei DR bestehen aus
3*(9+9) Ebenen (links, Mitte, rechts). Eine DR besteht aus 21 Elementen,durch
die Rundung entfallen 2 Punkte, die von den 21 Elementen abgezogen werden. Die
Zahl 19 kann sich auf die Doppelzählung der 9 Durchmesserelemente + 10 Radialelementen,
die Zahl 21 auf die Numerierung von 9 DM-Elementen (2+3+|2+3+1+3+2|+3+2)
beziehen.
4. Es besteht
nun die Aufgabe zu erklären, nach welchen Gesichtspunkten man die Produktzahlen
21*19 mit den jeweils 37 Elementen der beiden
Dezimaldreiecke (Tetraktys) in Übereinstimmung bringen kann.
In beiden Fällen geht es um einen zusätzlichen
Begrenzungspunkt für 10 ME bzw. 9 ME. Die einfachste Lösung ist, sich auf die
zwei Zählmöglichkeiten eines Tetraktysrahmens zu beziehen, indem man für die
Zahl 21 11P+10L annimmt und die Zahl 18 (9P+9L) um den Mittelpunkt erweitert.
Nach einer anderen Sichtweise geht man nur von den Punkten beider Dezimaldreiecke aus, einmal von den 2*9 = 18 Punkten beider
Tetraktysrahmen + gemeinsamem Mittelpunkt und einmal von 2*10 Punkten. Wie
kommt man nun zum 21. Punkt?
5. Die konkret
gestellte Frage soll auf abstrakter und prinzipieller Ebene beantwortet werden.
Jede Zahl besteht zunächst absolut für sich. Innerhalb der Existenz von Raum
und Zeit jedoch hat sie einerseits Zählfunktion ohne Beziehung zu Maßen,
andererseits dient sie der Bestimmbarkeit von
Maßeinheiten, wodurch es zur Doppelung von BP und ME kommt. Damit die Zahl des Begrenzungspunktes sich mit
der Zahl der vollendeten Maßeinheit deckt, bedarf es eines ideellen
Anfangspunktes, der nicht-zählbaren Null. Macht man die Null aber zählbar und
ersetzt sie durch die Zahl 1, ist der BP jeweils um 1 Zähler höher als das
erreichte Maß.
Die Formel für das ungerade Endergebnis von Zahl+Maß
lautet daher: 1+(2*Zahl) oder abstrakter: Zahl+1, da sich die Anzahl der BP mit den ME deckt, in ihnen also enthalten ist.
Im Mittelpunkt + den gleichvielen Punkten und Linien
(9+9) des Tetraktysrahmens ist die genannte Formel vollkommen verwirklicht.
6. Die beiden
Tetraktys sind in sich sichtbares geometrisches Zeichen und Programm für die
Verbindung von Zahl und Maß. Daher kann man die 10 Punkte der ersten Tetraktys
als Zahl und die 10 Punkte der gegenüberliegenden als Maß betrachten. Den
zusätzlichen Begrenzungspunkt erhält man, wenn man den Beginn der Zählung 1 und das Ende der Zählung – hier 20 – addiert. Damit ist auch gesagt, daß
es sich um eine Zahlenreihe von 1 bis 20 handelt.
Die beiden
Zahlen 219 und 180 scheinen das Problem des Zusatzpunktes sowie – in sehr
abstrakter Weise – der Zahlen 19 und 21 zu verdeutlichen, wenn man sie der
ZW/FW-Verrechnung unterzieht:
|
|
ZW |
FW |
Sm. |
Verhältnis |
|
|
219 |
76 |
|
|
|
|
180 |
15 |
|
|
|
Sm. |
399 |
91 |
490 |
10*49 |
|
FW |
29 |
20 |
49 |
1*49 |
Die Zahl 49 dürfte sich auf die 49 Elemente des Dezimalsterns
beziehen. Das Verhältnis 1:10 bezeichnet den ersten und letzten Punkt und damit
11 Begrenzungspunkte. Es könnte auch die Zahl der Maßeinheiten von 1 bis 10 bedeuten und damit gleichzeitig die
11 Begrenzungspunkte mit einschließen.
7. Im lateinischen
Alphabet wird das Prinzip, erster Zähler+letzter Zähler ergibt zusätzlichen BP,
in den Buchstaben A für 1. Punkt der
oberen Tetraktys und V für den 20. Punkt der unteren Tetraktys verwirklicht. Das "Doppelzeichen" X als Ergebnis von 1+20 trägt den 21 Elementen der DR Rechnung, zusammen
ergeben die Buchstaben AVX zwei
Doppelrauten, die auf die Bildung eines Oktaeders hinzielen.
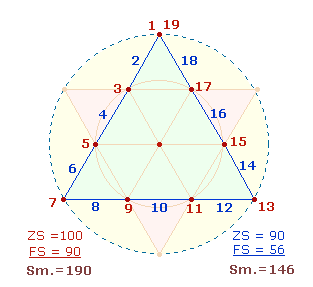
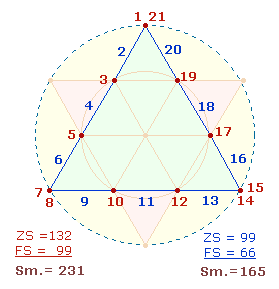
8. Die enge Beziehung zwischen 19 und 21 läßt sich erkennen, wenn man das Dezimaldreieck einmal von 1 bis 19 und
einmal von 1 bis 21 numeriert und ZW und FW nach Punkten und Linien
unterscheidet. Bei beiden Zahlenreihen zeigt sich nämlich, daß die ZW+FW der Liniennumerierung der Faktorensumme aller
Zahlen entspricht und ebenso die ZW+FW der Punktenumerierung der Zahlensumme aller Zahlen:
|
|
|
Die Gesamtsumme aller Zahlen und Faktoren beträgt 732 = 12*61. Die Faktorensummen der
Liniennumerierung ergeben 56+66 = 122 = 2*61, also ein
Sechstel der Gesamtsumme.
9. Wenn der
Tetraktysstern die Zahlen 19 und 21 als wesentliche Pfeiler des Dezimalsystems erweisen, dann bedeutet der
Kunstname VESTA nicht nur V EST A – V ist A, sondern in persönlicher Anrede ES TAV – Du bist das TAV: Gott wird angesprochen in zwei der bedeutendsten
Ordnungszahlen des Dezimalsystems, die im griechischen Buchstaben TAU vereint sind.
Erstellt: August 2001
Erweitert: Mai 2005