PENSATOR
II. Die 3
konzentrischen Zahlenpaare und die Zahlen 1-33
a) Achsenkreuze
d) 17 und 16
a) Achsenkreuze
1.
Die 3 konzentrischen Zahlenpaare (18-33, 19-32,
20-31) orientieren
sich an der Konzentrik der Grundzahlen 1-9 mit den Randzahlen 1-3 und 9-7. Die Zyklik des Dezimalsystems ist besonders in den Umkehrzahlen 12 und 21 erkennbar.
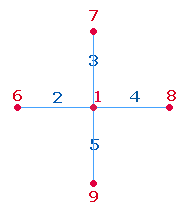
Die Mitte beider Zahlen, 16 und 17, haben ihre geometrische Gestalt im Achsenkreuz
5 mit 9 Punkten und 8 Linien je
Achse, insgesamt 17 Punkten und 16 Linien.
Es
handelt sich um das dritte Achsenkreuz, das sich aus dem Grundachsenkreuz von 5 Punkten und 4 Linien
entwickelt:
|
|
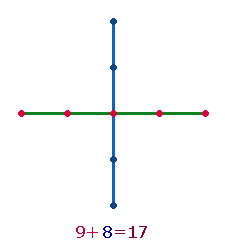
Die Zahl 9 ist der Ausgangspunkt für das
zweite Achsenkreuz, es besteht aus 9 Punkten und 8 Linien. Nun besteht eine Achse aus 9 Elementen:
|
|
2.
Die Zahl 17 ist wiederum Ausgangspunkt für das oben bereits erwähnte
Achsenkreuz aus 17 Punkten und 16 Linien. Die Zahl der Punkte ab
dem Mittelpunkt bestimmt die Bezeichnung Achsenkreuz 5 (AK5). Das AK4 mit 25 Elementen ist bei diesem
Entwicklungsschritt übersprungen. Jedes größere Achsenkreuz wird um 8 Elemente erweitert.
Folgende
zwei Aspekte sind im Hinblick auf das SATOR Quadrats zu beachten :
Erstens, werden nur die Punkte eines
Achsenkreuzes numeriert, wird es auf die Elemente seiner vorherige Stufe
zurückgesetzt.
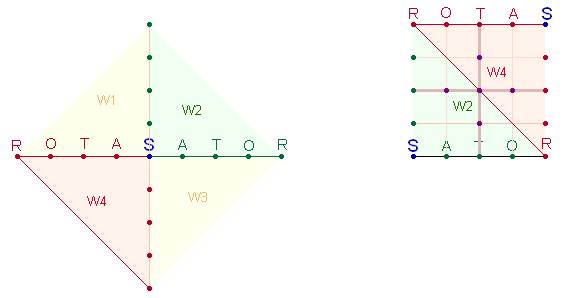
Zweitens, das Achsenkreuz aus 17 Punkten und 16 Linien ist mit dem SATOR Quadrat in logische Verbindung
zu bringen. Dies geschieht so: Verbindet man die Achsenenden durch Linien,
entsteht ein Rautenquadrat aus 4 rechtwinkligen Dreiecken. Durch Verschieben
eines Winkeldreiecks gegen das andere entsteht ein Quadrat, dessen weitere
Struktur durch horizontale und vertikale Verbindungslinien ergänzt zu denken
ist. Die Mittelachse dieses Quadrats fällt auf die Zahl der 9 Ausgangselemente zurück, erstens weil durch die Verschiebung die
Achsenkreuzachse halbiert wird – denn zwei Winkeldreiecke fallen nach dem
Verschieben weg – und zweitens, weil nur die Punkte mit Buchstaben besetzt werden:
|
|
3.
Die Summe der Zahlen von 1-33 ist 33*17 = 561.
Addiert man die Einzelziffern der ZS der 5 Wörter des SATOR-Quadrats (69,52,61,52,69),
erhält man 51 = 3*17. Das bedeutet, daß die 5 ZS mit ihren Umkehrzahlen 33*17 = 561
ergeben. Wenn wie bei den auf- und absteigenden Zahlen 69 und 52 die Differenz der
Einzelziffern gleich ist, ist auch die Umkehrsumme gleich: 69+52 = 121 und 96+25 = 121. Die
Differenz der beiden Gesamtsummen ergibt sich durch Hinzufügung der dritten
Zahl: 242+61 = 303; 242+16 = 258.
4.
Wenn die Zahl 17 die Mitte zwischen 1 und 33 einnimmt, ergibt sich die
Symmetrie 1-16 |17| 18-33.
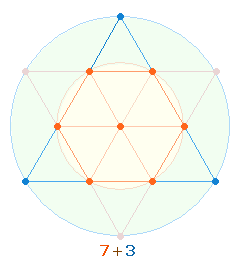
Man kann also für die Zahlen 1-16 ebenfalls drei konzentrische Zahlenpaare bilden: (1-16, 2-15, 3-14). Man erhält auf diese Weise
zweimal drei Randzahlen und – mit 17 – 7 Mittelpunktszahlen in der Folge 3-7-3, die der
Anordnung der beiden Tetraktys entspricht: jeweils 3 Eckpunkte und 7 Hexagonpunkte:
|
|
3 |
|
3 |
|
1 |
|
3 |
|
3 |
|
||||||||
|
Zahl |
1 |
2 |
3 |
6 |
14 |
15 |
16 |
45 |
17 |
57 |
18 |
19 |
20 |
96 |
31 |
32 |
33 |
221 |
|
FW |
1 |
2 |
3 |
6 |
9 |
8 |
8 |
25 |
17 |
36 |
8 |
19 |
9 |
55 |
31 |
10 |
14 |
139 |
|
sm |
6+55 = 61; 25+36
= 61 |
360 |
||||||||||||||||
Ohne die 17 des Mittelpunktes
beträgt konzentrisch von außen nach innen jede der beiden 6-er Einheiten die ZS+FS 102+61 = 163. Die Einzelziffern von 163 bezeichnen den Punkteaufbau einer Tetraktys, jeweils
Mittelpunkt, 6 Kreislinienpunkte und 3 Eckpunkte. Zweimal 61
ist auf die beiden
konzentrischen Kreise des Tetraktyssterns zu beziehen, denen jeweils 6 Kreislinienpunkte und
Mittelpunkt zugewiesen sind.
Die FS der 6 Zahlen der ersten und
der zweiten Hälfte betragen 6+25 = 31 und 36+55 = 91. Die Bedeutung beider Zahlen stimmt mit der
grundsätzlichen Struktur zweier Hälften einer Zahlenreihe bei gemeinsamem
Symmetriemittelpunkt überein: Das ZS-Verhältnis der ersten zur zweiten Hälfte einer
Zahlenreihe ist 1:3, was sich durch
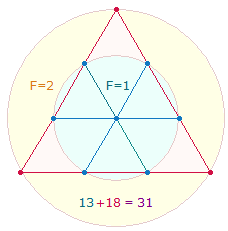
konzentrische Addition erkennen läßt: 1+16 = 17; 18+33 = 51. 1:3 beträgt auch das Flächenverhältnis der beiden konzentrischen Kreise des Tetraktyssterns.
Es wird wiedergegeben durch 7 Punkte des Hexagons und 13 Punkte des
Tetraktyssterns. 7 und 13 sind die beiden Faktoren der Zahl 91.
5.
Die ZS der 13 Zahlen ist 13*17 = 221, die FS 122+17 = 139. Auch die 10 Zahlen von 21-30 mit
der ZS 255 haben die FS 139. Die
Einzelziffern bezeichnen wohl den Aufbau des Tetraktyssterns aus Mittelpunkt, 3 Eckpunkten und 9 Punkten eines
Tetraktysrahmens. Die FS der
Zahlen 4-16 beträgt 71.
6.
Die FS der Zahlen 1-33 ist 349. Diese Zahl bezieht
sich besonders auf die 3 Seiten des Tetraktysrahmens mit 4 Punkten und 3 Linien je Seite und ist
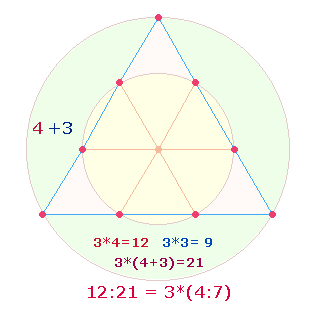
zu lesen als 3*4 = 12 Punkte + 9 Linien = 21.
Zusammen mit der ZS 561 erhält man die Summe 910 = 7*10*13.
Die ZS+FS der 13 Zahlen 221+139 beträgt 360,
die Differenz zu 910 550 (210+340).Teilt man beide Zahlen
durch 10,
ergeben sich mit 36 und 55 die FS der 6 konzentrischen Zahlen (18 19 20
– 31 32 33). 36 und 55 sind die Summen der
Zahlen 1-8 und
1-10.
Die beiden
ZS und FS sind bisher 221+255+139+139 = 754 =
58*13. Die
übrigen ZS+FS 12*13 ergibt sich aus den
Zahlen 4-13: 85+71 = 156.
7.
Sieht man das SATOR-Quadrat in Zusammenhang mit den Zahlen 1-33, so nimmt die ZS 182 der ersten drei Wörter
SATOR OPERA TENET bzw. die doppelte FS der 3 Zahlenpaare ein Fünftel der ZS+FS 910 ein.
8.
Wenn man die Zahlen 1-33 in Kreisform anordnet, gruppieren sich die Zahlen 1-3
und 31-33 zu einer Einheit und bilden mit den Zahlen 14-20 die Pole und die
Zahlen 4-13 sowie 21-30 die dazwischen liegenden Teile des Kreises. Die Werte
der letzteren sind:
|
|
ZS |
FS |
Sm. |
|
4-13 |
85 |
71 |
156 |
|
21-30 |
255 |
139 |
394 |
|
Sm. |
340 |
210 |
550 |
Die durch 10 geteilten ZS+FS 34 und 21 enthalten nicht nur die Zahlen 1-4, sondern lassen sich auf die Doppelraute
(DR) und die Flächenverhältnisse des Doppelkreises anwenden. Die 21 Elemente der DR stehen für die
Flächengröße 3, die 13 Elemente des
hexagonalen Bereichs und die 21 Elemente der ganzen DR für die Flächengröße 1+3. Auf diese Weise erhält man die trinitarischen Zahlen 3+4 = 7.
1.
Innerhalb der Zahlen 1-33 kommt der Zahlengruppe
von 12-21
wegen des Umkehrcharakters der ersten und letzten Zahl eine besondere Rolle zu:
Die ZS+FS der 10 Zahlen sind:
|
ZW |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
165 |
|
FW |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
10 |
108 |
|
sm |
19 |
26 |
23 |
23 |
24 |
34 |
26 |
38 |
29 |
31 |
273 |
|
|
|
156 = 12*13
= 6*26 |
|
|
|
|
|||||
|
165 = 15*11; 108 =
12*9; 273 = 21*13 |
|||||||||||
Die ZS der 10 Zahlen, die die 10 Punkte der Tetraktys
repräsentieren, ist mit 15*11 die Umkehrsumme zu 51*11 der Zahlen 1-33. Das ZS+FS-Verhältnis der 23:10 Zahlen ist 637:273 = 7*13*(7:3). Man erkennt in den Verhältniszahlen leicht den Bezug
auf sieben Punkte des Hexagons, zu denen durch Erweiterung der Segmentlinien
drei Eckpunkte der Tetraktys hinzukommen:
|
|
Die
Einzelziffern des Produkts 13*21 geben die zwei trinitarischen Flächenverhältnisse der beiden
Tetraktyskreise wieder, die ganzen Zahlen das Kreisflächenverhältnis 1:3.
Das Produkt 12*9 der FS 108 weist auf eine Besonderheit der drei
Tetraktysseiten hin: Jede einzelne Seite besteht aus 4 Punkten und 3 Linien, somit ergibt
sich für drei Seiten die Zahl von 21 Elementen. Wenn die Punkte zur Gesamtheit der
Elemente der drei Seiten in Bezug gesetzt werden, kommt das Verhältnis 12:21 zustande:
|
|
2.
Die Zahl 108 als ZS+FS kommt auch durch die konzentrischen Außen- und
Innenglieder zustande:
|
ZW |
12 |
16 |
17 |
21 |
66 |
|
FW |
7 |
8 |
17 |
10 |
42 |
|
sm |
19 |
24 |
34 |
31 |
108 |
|
42:66 = 6*(7:11) |
|||||
Das
Verhältnis 7:11 bezieht sich auf eine Rautenfigur der
hexagonalen Erweiterung. Die 7 Elemente des Dreiecks werden um 4 Elemente zu 11 erweitert. Dem
Verhältnis 7:11, d.h. dem Teils zum Ganzen, entspricht das
Kreisflächenverhältnis 1:3.
3.
Die ZS+FS der Zahlen 13
und 18 sind jeweils 26, ihr FS:ZS-Verhältnis beträgt 21:31. Die dazwischen liegenden
vier Zahlen haben ebenfalls die durchschnittliche ZS+FS 26. Deren FS:ZS-Verhältnis ist 42:62 = 2*(21:31). Somit entsprechen den 2:4 Zahlen dieselben FS:ZS-Verhältniszahlen 21:31 als Umkehrung der Produktzalen 12*13 der Gesamtsumme 156. In den Einzelziffern
der Verhältniszahlen begegnen wieder die beiden oben genannten trinitarischen
Verhältnisse der Kreisflächen. Den Symmetriemittelpunkt der 6 Zahlen bilden 15+16 für die Zahlenreihe 1-30.
Das ZS+FS-Verhältnis der 6:4 Zahlen beträgt 156:117 = 13*(12:9). Auch
hier ergibt sich aus der Teilzahl 6 zur
Gesamtzahl 10 das Verhältnis 12:21.
Auch die Werte der
unteren und oberen drei Zahlen bilden Verhältnisse:
|
13 |
14 |
15 |
42 |
16 |
17 |
18 |
51 |
|
13 |
9 |
8 |
30 |
8 |
17 |
8 |
33 |
|
26 |
23 |
23 |
72 |
24 |
34 |
26 |
84 |
|
72:84 = 12*(6:7) |
|||||||
Ein FS:ZS-Verhältnis
zeigt sich auch zwischen den Mittelpunktzahlen 15-17 und den drei übrigen Zahlen:
|
15 |
16 |
17 |
48 |
13 |
14 |
18 |
45 |
|
8 |
8 |
17 |
33 |
13 |
9 |
8 |
30 |
|
23 |
24 |
34 |
81 |
26 |
23 |
26 |
75 |
|
81:75 = 3*(27:25) |
|||||||
4.
Die Zahl 13 wird durch die Zahl 18 umfaßt, indem die drei Hexagonachsen aus 13 Elementen (7 Punkten + 9 Linien) und der
Tetraktysrahmen aus 18 Elementen (9 Punkten + 9 Linien) besteht:
|
|
5.
Fügt man den 10 Zahlen noch die 11. Zahl 22 hinzu, ergibt sich die ZS 165+22 = 187, die FS 108+13
= 121, das FS:ZS-Verhältnis 11*(11:17) und der
durchschnittliche ZW+FW 28.
6.
Erweitert man die 10 Zahlen konzentrisch um
jeweils 4,
erhält man folgendes Ergebnis:
|
ZW |
8 |
9 |
10 |
11 |
165 |
22 |
23 |
24 |
25 |
297 |
|
FW |
6 |
6 |
7 |
11 |
108 |
13 |
23 |
9 |
10 |
193 |
|
sm |
14 |
15 |
17 |
22 |
273 |
35 |
46 |
33 |
35 |
490 |
Das ZS+FS-Verhältnis 273:217 ist 7*(39:31). Nimmt man die ZW+FW 35 zu 273 hinzu – wie oben
geschehen – beträgt das FS:ZS-Verhältnis von 11:7 Zahlen 308:182 = 14*(22:13). Die
Einzelzahlen geben das Verhältnis von Kreisflächeneinheiten zu Radialelementen wieder: 2
Flächeneinheiten und 2 Radialelemente des äußeren Kreisrings, 1
Flächeneinheit und 3 Radialelemente für den hexagonalen Kreis.
18:15
Zahlen haben das ZS+FS-Verhältnis 490:420 = 70*(7:6). Die Verhältniszahlen
sind auf 7 Hexagonpunkte und 6 Erweiterungspunkte beziehbar.
Die FS 193 stellt eine Umkehrung zu 139 dar
und bezeichnet die Gliederung der 13 Punkte des Tetraktyssterns.
Die ZW+FW 14 und 35 sind
durch 7
teilbar und stellen einen Rahmen für die dazwischen stehenden Zahlen, deren
Summe 168
beträgt und zur übrigen Summe 322 das Verhältnis 14*(12:23) = 14*35 hat.
1.
Die konzentrische Erweiterung um 8 Zahlen von 12 und 21 aus, die von den Mittelpunktszahlen
17 und 16 erfolgte, entspricht
einer Zahlenreihe von 1 bis 32, erreicht also nicht die Zahl 33. Es überlagern sich
somit, vom Mittelpunkt her gesehen, zwei Zahlenreihen. Die ZS+FS der zweiten Zahlenreihe 528+335 = 863 ist eine Primzahl.
Streng
genommen dürfte also die ZS+FS 490 nicht auf die Gesamtsumme 910 der Zahlenreihe 1-33 bezogen werden. Nun
gehören jedoch aus zwei Gründen die Zahlen 16 und 17 wie Zwillinge zusammen, die das Zahlenverhältnis
rechtfertigen können.
Erstens, zwei Zahlenreihen, von denen die erste bis zu einer geraden Zahl reicht,
teilt mit der nächst höheren denselben Multiplikationsfaktor: 1-16 = 8*17,
1-17 = 9*17.
Zweitens, eine vielleicht einzigartige Besonderheit besteht
darin, daß die FS 102 = 6*17 der Zahlen 1-16 den Faktor der nächsten Zahl 17 enthält. Auf diese Weise beträgt
das FS:ZS-Verhältnis der beiden Reihen (102+119):(136+153) = 17*(13:17) = 510 =
10*51 gegenüber 11*51 der Zahlen 1-33.
2.
Der Sinn dieser besonderen Konstellation besteht
wohl in dem Ausgangsmodell der 9 Punkte + 8 Linien, der bereits im ersten Teil behandelt wurde:
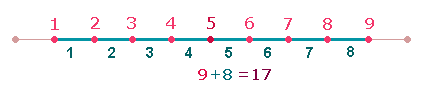
Zur
Erklärung der beiden Zahlen 17 und 16 sind allerdings nur die Grundzahlen von 1-9 zuständig, die sich
konzentrisch von außen nach innen zu 10 addieren: 1+9, 2+8, 3+7, 4+6. Den beiden
trinitarischen Kreisflächenverhältnisse 1:2 und 1:3 entsprechen die komplementären Additionen 9+8 = 17 und 9+7 = 16. Die Addition beider
komplementären Gruppen ergibt 7+33. Die Einzelziffern bezeichnen die Gliederung der 13 Punkte des Tetraktyssterns. Die Umkehrzahlen 733, 337, 373 sind prim.
Von den beiden
zusammengesetzten Zahlen können die FW ermittelt werden, woraus folgendes Ergebnis
zustande kommt:
|
|
|
|
sm |
|
|
sm |
GS |
|
ZW |
9 |
8 |
17 |
9 |
7 |
16 |
33 |
|
FW |
6 |
6 |
12 |
6 |
7 |
13 |
25 |
|
|
|
|
29 |
|
|
29 |
58 |
Die
Einzelziffern der FS 12 und 13 geben wiederum die Ausgangsflächenverhältnisse 1:2 und 1:3 wieder. Die Zahlen 17+12 sind in einem numerierten Achsenkreuz und dem Rahmen eines Doppelrautenkreuzes anzutreffen, die Zahlen
16+13 in
einem weiteren Doppelrautenkreuz.
Die 4W-Summen der beiden
Zusammensetzungen sind:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
ZW |
17 |
12 |
29 |
17 |
7 |
24 |
53 |
|
FW |
16 |
13 |
29 |
8 |
13 |
21 |
50 |
|
|
33 |
25 |
58 |
25 |
20 |
45 |
103 |
|
25:20 = 5*(5:4); 24:21 = 3*(8:7) |
|||||||
Die
Gesamtsumme 103 zeigt durch 10+3 die Punktezahl des Tetraktyssterns an.
3.
Die beiden Zahlenreihen 1-33 und 1-32 erzielen folgende
Ergebnisse:
|
|
1-33 |
1-32 |
|
||||
|
|
ZS |
FS |
sm |
ZS |
FS |
sm |
GS |
|
|
561 |
349 |
910 |
528 |
335 |
863 |
1773 |
|
FW |
31 |
349 |
380 |
22 |
72 |
94 |
474 |
|
sm |
|
|
1290 |
|
|
957 |
2247 |
|
1290 = 10*3*43 |
|||||||
|
2247 = 21*107 |
|||||||
Aus der
Summe 1290
lassen sich die 10 Punkte der Tetraktys und die 3*7 Elemente der
Tetraktysseiten ablesen, aus der Gesamtsumme 2247 ebenfalls die 3*7 Elemente der Tetraktysseiten, die 10 Punkte der Tetraktys + 7 Punkte des Hexagons.
Erstellt: November 2005
Überarbeitet: Juli 2014