DAS SATOR-QUADRAT

PENSATOR

I. Die 8 verschiedenen Buchstaben des SATOR-Quadrats

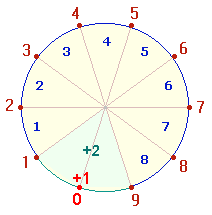
II. Die 3 konzentrischen Zahlenpaare und die Zahlen 1-33

III. Die Zahl 5

IV. 8+17 Buchstaben

a) 17+9

b) 17+8

c) Zweimal drei "Fischfiguren"

V. Die Zusammensetzung von PENSATOR

VI. Ergänzungen

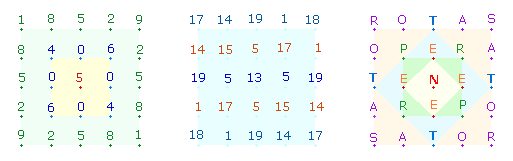
I. Die 8 verschiedenen Buchstaben des SATOR-Quadrats

1. Der Satz SATOR OPERA TENET enthält 8 verschiedene Buchstaben. Stellt man vor SATOR die drei übrigen Buchstaben der Reihenfolge ihres ersten Auftretens nach, erhält man das Wort PEN-SATOR, das eine Substantivierung des Verbs pensare – abwägen, im Gleichgewicht halten, vergelten, beurteilen darstellt, selbst aber in der lateinischen Literatur nicht belegt ist. Es werden offensichtlich zwei Eigenschaften Gottes genannt: Er hält die kosmischen Kräfte im Gleichgewicht und er wägt die Taten und Verdienste der Menschen.

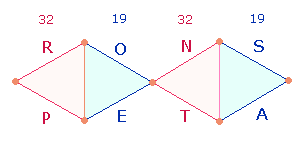
2. Das Besondere am Wort PENS|ATOR ist, daß jede Hälfte die Zahlensumme (ZS) 51 hat und daß die ZS von je zwei Buchstaben jeder Hälfte wiederum gleich sind:

P	E	N	S	A	T	O	R
1	2	3	4	5	6	7	8
a		b		a		b
15	5	13	18	1	19	14	17
20		31		20		31

Das Muster ab gilt parallel für jede Hälfte. Nimmt man von jeder Hälfte zweimal je zwei Buchstaben (PE-OR, NS-AT) zusammen, ist das Muster der äußeren zu den inneren Buchstaben ab|ba.

3. Dem Muster abab stellt sich ein weiteres zur Seite. Es ist sowohl parallel als auch chiastisch: Beide Hälften haben das Muster abba. Der ZS der umschließenden Buchstaben (aa) der ersten Hälfte entspricht die ZS der umschlossenen Buchstaben (bb) der zweiten Hälfte, und die umschlossenen Buchstaben der ersten Hälfte werden zu umschließenden der zweiten Hälfte.

P	E	N	S	A	T	O	R
1	2	3	4	5	6	7	8
a	b	b	a	a	b	b	a
15	5	13	18	1	19	14	17
	18				33

Man kann als zusammengehörig aber auch die äußeren und inneren Buchstaben jeder Hälfte ansehen: 15+18, 1+17; 5+13, 19+14. Die ersten vier Buchstaben können zu PARS – Teil geordnet werden.

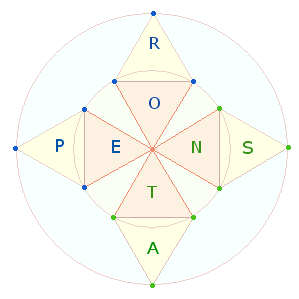
4. Ein drittes Muster erstreckt sich über beide Hälften. Es wird erkennbar, wenn man die 8 Buchstaben auf den Rahmenlinien der Doppelraute (DR) umlaufend anordnet:

Dieses Muster ist konzentrisch, indem die zwei äußeren und zwei inneren Buchstaben dieselbe ZS haben wie die zweimal zwei Buchstaben dazwischen:

P	E	N	S	A	T	O	R
15	5	13	18	1	19	14	17

In der DR-Anordnung verläuft die ZS-Abfolge parallel.

5. Rechnerisch ist bisher nicht geklärt, ob diese komplexen Beziehungen von zweimal 4 Zahlen eine einmalige Konstellation darstellen oder mit anderen Zahlen wiederholt werden können. An der Summengleichheit ändert sich nichts, wenn jede der vorliegenden Zahlen gleichmäßig erhöht wird.

Die Eigenschaften der 8 Zahlen können folgendermaßen beschrieben werden:

Die niedrigste Zahl ist 1, die höchste 19. Die Zahlen 19 und 18 lassen sich jeweils zweimal zusammensetzen:

19 = 1+18; 19 = 5+14

18 = 1+17; 18 = 5+13

Übrig bleibt die Zahl 15.

Zweimal drei Zahlen bilden konzentrische Paarungen mit dem Mittelwert 16:

13 14 15 – 17 18 19

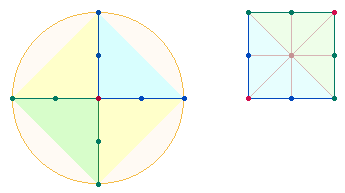
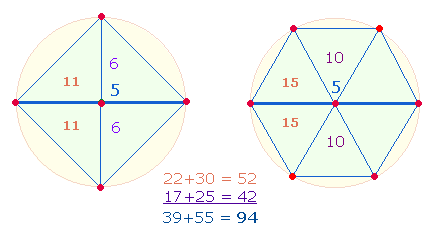
6. Das Modell für die Ausgewogenheit der 8 Buchstaben/Zahlen sind die 8 Flächen des Oktaeders, der aus einem DR-Kreuz zusammengefügt werden kann:

Die 8 Buchstaben sind von links nach rechts und von unten nach oben in die Dreiecksflächen eingetragen. Das Gleichgewicht der 8 Buchstaben besteht darin, daß die ZS der oberen Pyramide des Oktaeders, die aus den äußeren Dreiecken besteht, dieselbe ist wie die der unteren. Aber auch zweimal vier Flächen, die den Oktaeder umschließen, haben dieselbe ZS.

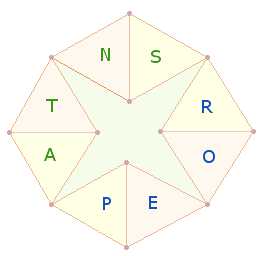
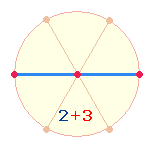
Verschiebt man zwei Rautenwinkel gegeneinander, erhält man ein Oktogon. Die untere Raute bildet nur mit der rechten die ZS 51, aber nicht mit der linken:

Zweimal zwei Buchstaben jeder Worthälfte stehen einander nun vertikal und horizontal gegenüber.

7. Die drei Muster ergeben 6 Additionsergebnisse, die konzentrisch in zwei Paaren von je drei Zahlen aufeinander folgen:

18	19	20	31	32	33
EN	EO	PE	NS	PR	PS
AR	SA	AT	OR	NT	TO

Von besonderem Interesse sind die FW der konzentrischen ZS-Paare. Die roten Buchstaben gehören der linken, die blauen der rechten Hälfte von PENS|ATOR an:

	ZS	FW		ZS	FW	GS
PE/AT	20	9	NS/OR	31	31	91
EO/SA	19	19	PR/NT	32	10	80
EN/AR	18	8	PS/TO	33	14	73
sm	57	36		96	55	244
36+55 = 91; 2*91 = 182
244 = 4*61

Die Faktorensummen (FS) 36 und 55 sind die Summen der Zahlen 1-8 und 1-10. Die Einzelziffern der Gesamt-ZS+FS 244 zeigen die Linienstruktur der Doppelraute. Von den 8 Maßeinheiten liegen 2 außerhalb der Grundzahlen, eine geht von der 0 aus, die andere kehrt zur 0 zurück:

Der bedeutende Faktor 61 ist die ZS einer TENET-Achse, seine Einzelziffern sind wohl mit den 7 Punkten der DR gleichzusetzen. Eine tiefergehende Möglichkeit besteht auch in 6 Ecken + 1 Volumen des Oktaeders.

Die Gesamt-FS 91 wurde nur für ein Buchstabenpaar ermittelt und ist daher auf 182 zu verdoppeln. Damit scheint ein logischer Begründungszusammenhang zu der ZS+FS 102+80 von PENSATOR und der ZS 182 von SATOR OPERA TENET zu bestehen.

182 als ZS+FS ergeben auch die Initialen SOT-TOR der Leseweise

SATOR OPERA TENET

TENET OPERA ROTAS

	ZS	FW
SOT	51	36	87
TOR	50	45	95
sm	101	81	182

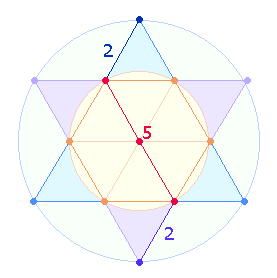
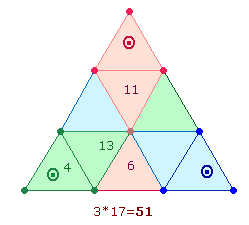
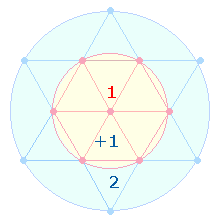
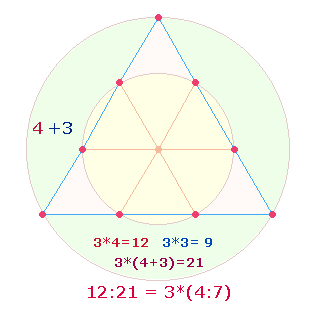
8. Die Zahl 91 = 7*13 ist die Summe der Zahlen 1-13. Sie bezieht sich insbesondere auf die 13 Punkte des Tetraktyssterns, der sich innerhalb zweier konzentrischer Kreise befindet, deren Flächen sich wie 1:3 verhalten. Das Flächenverhältnis wird durch die beiden Produktzahlen 7 und 13 treffend bezeichnet. Denn die 7 Punkte des Hexagons vertreten die Flächeneinheit 1, die 13 Punkte des gesamten Tetraktyssterns die Flächeneinheit 3:

Eine weitere Bedeutung der Zahlen 7 und 13 ergibt sich aus folgender Überlegung: Da sich zwischen innerem und äußerem Kreisbogen ein Kreisring von der Flächengröße 2 befindet, zeigen beide Kreisbogen auch ein Flächenverhältnis 1:2 an. Die Addition beider Verhältnisse ergibt (1+3)+(1+2) = 7. Der innere Kreis besteht aus 3 Radialelementen, die durch den äußeren Kreis um je 2 auf 5 erweitert werden. Wendet man diese Zahlen auf die Flächenverhältnisse an, erhält man (3+5)+(3+2) = 5+8 =13. Da ein Kreis jedoch aus 2 Radien besteht, sind diese beiden Zahlen zu verdoppeln. Im SATOR-Quadrat werden beide Zahlen zunächst multipliziert (7*13) und das Ergebnis dann verdoppelt (182).

III. Die Zahl 5

1. Wenn man die Zahl 5 oder eine andere Zahl nennt, wird man ohne Nachdenken damit etwa 5 Bücher auf einem Tisch oder einen Würfel von 5 cm Kantenlänge bezeichnen. In Wirklichkeit handelt es sich bei dem einen um eine Anzahl von Objekten und bei dem anderen um Maßeinheiten. Diese aber sind nur zählbar, wenn sie durch voneinander durch Punkte abgegrenzt sind. Das Erfassen von Maßeinheiten ist also immer abhängig vom Vorhandensein von Begrenzungspunkten.

Im römischen Zählsystem ist die Zahl 5 (V) die erste zusammenfassende Zähleinheit nach der 1 (I). Es gibt offensichtlich drei Möglichkeiten sie zu verstehen: Erstens als Erfassen von Objekten, zweitens als Kombination von Begrenzungspunkten und Maßeinheiten und drittens nur als Begrenzungspunkte für Maßeinheiten. Hier geht es nur um die zweite und dritte Möglichkeit.

2. Da alle Zahlenwirklichkeit von der Kreisteilung ausgeht, haben die 5 Elemente der Kreisachse Vorrang. "Elemente" soll als Oberbegriff für Punkte, Maßeinheiten (Linien) und Flächen verwendet werden:

In den 5 Elementen der Kreisachse ist die dritte Möglichkeit zur nächsten Kreisunterteilung bereits angelegt, die zum Achsenkreuz führt:

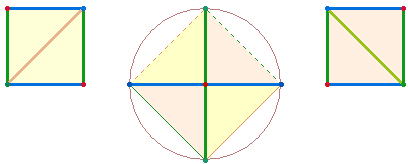
Das Achsenkreuz erweitert die 5 Ausgangselemente um 2*2 Elemente. Durch Winkelverschiebung nach links oder rechts entsteht jeweils ein Quadrat.

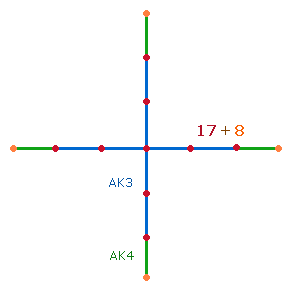
3. Das einfache Achsenkreuz aus 9 Elementen stellt die Grundzahlen von 1-9 dar. Diese werden darin vollendet, daß 9 Punkte 8 Maßeinheiten begrenzen. Das einfache Achsenkreuz aus 9 Elementen ist daher um 8 Elementen zum nächst größeren AK3 zu erweitern:

Das AK3 ist das erste mit einem Mittelpunkt und einem horizontal-vertikalen Achsenkreuz. Es besteht wie das Hexagon aus 25 Elementen: 9 Punkten, 12 Linien und 4 Einzelquadraten.

Das einfache Achsenkreuz kann auch als eine Darstellungsweise angesehen werden, um die Erweiterung des Hexagons zum Tetraktysstern oder Hexagramm zu kennzeichnen:

Der Durchmesser des Hexagramms besteht aus einer Zickzacklinie, die mit einer zweiten zwei Rautenfiguren bzw. eine Doppelraute (DR) umgrenzen. Das Hexagramm erhält seine besondere Bedeutung durch zwei konzentrische Kreise, deren Flächenverhältnis 1:3 beträgt. Es ist eine wesentliche geometrische Veranschaulichung des einen Gottes in drei Personen.

4. Charakteristisch für den Zickzackdurchmesser des Hexagramms sind 5 Punkte. Wenn nun die Konzentrik zweier Kreise auf das Quadrat übertragen werden soll, ist das AK3 zum AK5 zu erweitern:

Wie der Zickzackdurchmesser des Tetraktyssterns bestehen die Quadratseiten des SATOR-Quadrats aus 5 Punkten und 4 Maßeinheiten. Im Vergleich besteht das Hexagramm aus 49, das AK5 aus 81 Elementen, zusammen 130: Punkte 13+25 = 38, Linien 24+40 = 64, Flächen 12+16 = 28.

IV. 8+17 Buchstaben

a) 17+9

1. Bevor die Bedeutung der 8 verschiedenen Buchstaben und der 17 übrigen geklärt werden kann, ist auf die Addition 17+9 einzugehen.

Die Grundzahlen 1-9 sind als komplementär anzusehen:

17+9 = (9+8)+9 sind also die Komplementärzahlen zu (1+2)+1. 1:2 ist das Kreisflächenverhältnis des Hexagrammkreises, aufgeteilt in den hexagonalen und den Erweiterungsbereich; es bleibt noch die Flächeneinheit 1 des hexagonalen Kreises selbst:

2. 17+9 bezieht sich besonders auf die 26 Elemente des Oktaeders: Aus 9 Elementen besteht ein pyramidaler Aufbau, aus 8 Elementen die gemeinsame Mittelbasis, aus weiteren 9 die zweite Pyramide.

b) 17+8

1. Die Addition 17+8 hat zwei verschiedene Bedeutungen:

· Das AK3 kann durch 8 Elemente zum AK4 erweitert werden:

Eine Seite des dazu gehörigen Quadrats besteht aus 4 Punkten und 3 Linien, ebenso wie eine Tetraktysseite. Die Einzelziffern der 13 Punkte und 12 Linien des AK4 geben die zwei Kreisflächenverhältnisse des Tetraktyssterns wieder. Das erste Verhältnis rechnet den hexagonalen Kreis innerhalb des ganzen äußeren Kreises, das zweite nur die Aufteilung zweier Kreisausschnitte im Verhältnis 1:2.

Das Quadrat Q4 besteht aus 16 Punkten, 24 Linien und 9 Quadraten, zusammen aus 49 Elementen wie das Hexagramm.

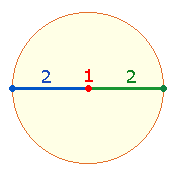
· Die Zahlen 1+2 als Ausgangszahlen der Komplementärzahlen 9+8 beziehen sich auf die 3 Radialelemente des Kreises:

Die 3 Radialelemente werden durch 2 weitere Elemente zu 5 Durchmesserelementen ergänzt. Das Verhältnis von 3+2 Durchmesserelementen wird im Hexagramm weiterentwickelt einaml zu 3+2 Radialelementen und einmal, nach dem Prinzip die Teils zum Ganzen, zu 3+5 Radialelementen.

Das Prinzip 3+5 ist auch in den 8 verschiedenen Buchstaben des SQ vorhanden. Es gibt 3 Vokale AEO und 5 Konsonanten PSTR sowie 3 Nicht-Primzahlen OPS und 5 Primzahlen AENTR.

2. Die zwei Additionen 17+9 und 17+8 ergeben 26+25 = 51. Ihnen entsprechen die Ausgangszahlen 4+5 = 9. Es sind dies einerseits die 4 Erweiterungselemente der Zickzackdurchmessers des Hexagramms und die 5 hexagonalen Durchmesserelemente, andererseits die 4 Linien und 5 Punkten einer Seite des SATOR-Quadrats.

3. Dem einfachen Kreis eingeschrieben werden können ein Rautenquadrat aus 17 Elementen und das Hexagon aus 25 Elementen:

Die in die Geheimnisse des SQ Eingeweihten kannten wohl auch die folgende Rechnung, bei der die ZS und Faktorensummen (FS) der Zahlen 1-17 und 1-25 ermittelt werden:

	ZS	FS	sm	FW1	FW2	sm
1-17	153	119	272	23	24	47
1-25	325	220	545	23	20	23
	478	339	817	46	44	90
817 = 19*43

Die Zahlen 17 und 25 stehen also in konzentrischer Beziehung zueinander wie die beiden Tetraktyskreise. Es ist bemerkenswert, daß die 4Werte der lateinischen Namen der drei göttlichen Personen 817 beträgt.

c) Zweimal drei "Fischfiguren"

1. Das Flächenverhältnis des hexagonalen Kreises zu dem Kreisring des äußeren Kreises ist 1:2. Durch die Erweiterung des Hexagons zum Hexagramm kommt eine neue geometrische Figur hinzu, die sich in der Tetraktys und in der DR befindet. Sie entsteht, indem zu einem hexagonalen Doppeldreieck ein weiteres Dreieck tritt, es sich also das Verhältnis von 2:1 Dreiecken handelt und die drei göttlichen Personen symbolisiert. 1:2 Dreiecke sind es, wenn man von jeder Tetraktysecke ausgeht:

2. Eine Fischfigur besteht aus 17 Elementen. Durch gegenseitige Verschränkung ergibt sich für zwei Tetraktys 2*51 = 102.

V. Die Zusammensetzung von PENSATOR

1. PENSATOR setzt sich zusammen aus dem bereits vorhandenen Wort SATOR und der Silbe PEN, die SATOR vorangestellt wird. Durch Teilung des Wortes in zwei Hälften wird das S der Silbe PEN hinzugefügt. Das ist nicht nur wegen des gleichen ZS 51 sinnvoll, sondern weil das S zum Wortstamm des Verbs PENS-ARE gehört. Im Wort SATOR ist das S der einzige Stammlaut, der im Partizip Perfekt Passiv vom Verb SER-ERE – säen übrig bleibt, doch kann man ihn nicht sinnvoll vom Rest des Wortes –ATOR trennen, da der ZS 69 als ganzer gesehen werden muß.

2. Auch wenn also das S zum Stamm PENS- gehört, ist die Zusammensetzung PEN+SATOR wegen der ZS von Bedeutung. Das Verhältnis der beiden Teil-ZW ist 33:69 = 3*(11:23) = 3*34. Die Zahl 3 bezieht sich auf die 3 Kreisachsen, die Zahlen 11 und 23 auf die Doppelzählung von Durchmesser- und Radialelementen, unnumeriert und numeriert. Bei den Radialelementen werden 2 Mittelpunkte gezählt:

3. Durch Hinzufügung der Silbe PEN ergeben sich 3 Buchstabengruppen mit angrenzenden ZS: PEN (33), SR (35), ATO (34). Addiert man von diesen Buchstabengruppen jeweils ihre Positionen in dem Wort PENSATOR, erhält man die Zahlenfolge 6, 12, 18 = 6*(1:2:3) = 36. Setzt man die Buchstabenzahl jeder Gruppe zu einer 3-stelligen Zahl zusammen, ergibt sich die Zahl 323 mit dem FW 36.

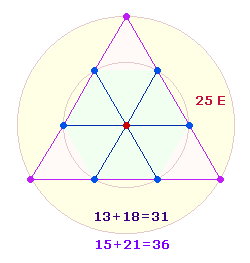
4. Die Anbindung des S an die Silbe PEN entspricht auch einem geometrischen Zusammenhang: Den spiegelbildlich verwandten Buchstaben N und S liegen die 3 Kreisachsen zugrunde, in deren Endpunkten die Tetraktys verankert ist:

Rechnet man für jede Achse einen Mittelpunkt und jede Tetraktysseite 4 Punkte + 3 Linien, ergeben sich die Zahlen 15 und 21. Zieht man die 6 gemeinsamen Punkte von 31 ab, bleiben 25 Elemente übrig.

5. Die Aufteilung 33+69 zeigt sich auch in der alphabetischen Anordnung von 4+4 Buchstaben:

A	E	N	O	P	S	T	R
1	5	13	14	15	18	19	17
33				69

VI. Ergänzungen

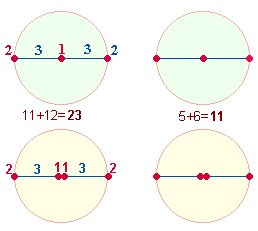
1. Wesentlich für das SATOR-Quadrat sind folgende Prinzipien:

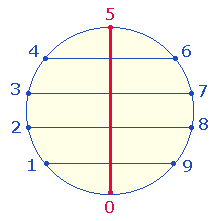
· Die Umkehrzahlen 12 und 21, wie sie aus dem folgendem Grundmuster zweier Kreishälften hervorgeht:

Der erste Halbbogen besteht aus 12, der zweite aus 21. Eine so gekennzeichneter Kreisbogen symbolisiert die Unendlichkeit Gottes. Der Zahl 102 entspricht die ZS der 8 verschiedenen Buchstaben.

· Die Konzentrik des Kreises und des Quadrats. Konzentrik bedeutet, daß die jeweils innere Figur von der äußeren wiederholt wird. Im Fall der beiden Tetraktyskreise ist das Kreisflächenverhältnis 1:3 und steht somit für die Einheit und Gemeinschaft dreier göttlicher Personen.

· Entsprechend den beiden Tetraktyskreisen ist auch das SQ als zwei konzentrische Quadrate konzipiert.

· Manche Zahlenverhältnisse, besonders das Verhältnis 12:21 ist ebenfalls inklusiv angelegt.

· Für Gesamtkonzeption sind FS von wesentlicher Bedeutung.

· Wie die zusammengesetzte Zahl 102 zeigt, kehren wesentliche Elemente des Zahlensystems in verschiedenen Entwicklungsstadien wieder. Z.B. die Zahl 17: Elemente des Rautenquadrats, des Achsenkreuzes, der Fischfigur, Numerierungssumme einer Tetraktysseite, Elemente einer Oktaederhälfte.

2. Das SQ beruht also auf einem Achsenkreuz aus 17 und aus 33 Elementen. Ihre ZS sind 9*17 und 33*17, was einem Verhältnis von 51*(3:11) = 51*14 = 42*17 = 714 = FW 12+17 = 29. Die entsprechenden FS sind 349+119 = 468 = 36*13 = FW 10+13 = 23. Die ZS von OP-ERA setzt sich zusammen aus 29+23 = 52. Das FS:ZS-Verhältnis 468:714 beträgt 6*(78:119) = 6*197. Das aus 33 Elementen gebildete Quadrat besteht aus 81 Elementen, der Zuwachs ist demnach 48. Es ergibt sich somit das Verhältnis (17+33):(8+48) = 50:56 = 2*(25:28) = 2*53 = 106.

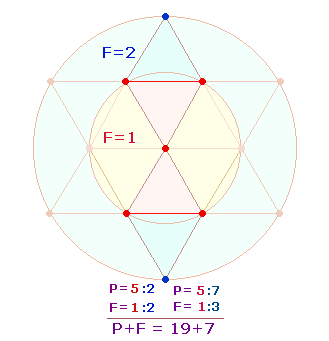
Der Faktor 197 erscheint ein weiteres Mal, wenn man die ZS+FS der Zahlen 21-30 bestimmt: ZS ist 5*51 = 255, die FS 349-(119+91) = 349-210 = 139; 255+139 = 394 = 2*197. Werden die ZS+FS der Zahlen 1-17 also nach konzentrischer Regel zweimal gerechnet, ist das ZS+FS-Verhältnis von 34+6 = 40 Zahlen zu 10 Zahlen 394*(2:1). Die Zahl 197 ist in 19+7 zu teilen und bedeutet die Entsprechung von 19 DR-Punkten zu 7 Kreisflächeneinheiten:

Die FS 139 der 10 Zahlen von 21-30 sind auf 10 Maßeinheiten des rechtwinkligen und des hexagonalen Achsenkreuzes zu beziehen.

3. Was die Zahlen 1-33 am deutlichsten mit dem Hexagramm verbindet, ist die FS 349. Diese Primzahl ist zu verstehen als 3*4+9 und sowohl auf die Tetraktysseiten als auch auf die Doppelraute beziehbar: Wenn man die 3*4 = 12 Punkte und die Gesamtzahl von 12 Punkten + 9 Linien addiert, erhält man das Verhältnis 12:21:

Ähnlich verhält es sich mit den 4*3 "Dachelementen" und den 9 vertikalen Elementen der DR:

Die ZS+FS der Zahlen 1-33 ist 561+349 = 910. Ein Zehntel dieser Summe betragen die FW der Zahlen 18-20 und 31-33. 91 ist die Summe der Zahlen der 1-13 Hexagrammpunkte. Die Faktoren 7*13 geben überdies das Kreisflächenverhältnis 1:3 der beiden konzentrischen Tetraktyskreise wieder.

Die Differenz zwischen 349 und 91 ist 258 = 6*43. Man kann die Faktoren als 6*(4+3) = 42 Rahmenelemente zweier Tetraktys ansehen, aber auch als 15 Rahemenelemente der DR: 2+5 Punkte + 8 Linien.

Die Einzelziffern der ZS der 5 SQ-Wörter 69+52+61+52+69 ergeben addiert 51. Kehrt man diese Werte um, ist die Summe beider 51*11 = 561. Die Differenz der ZS 303 des SQ zu 561 ist 258.

4. Die Anwendung des konzentrischen Prinzips auf das SQ zeigt folgendes Ergebnis:

	ZS	FS
inn. Qu.	97	83	180
ganzes Qu.	303	249	552
	400	332	732
83:249 = 83*(1:3)
332:400 = 4*(83:100)
180:552 = 12*(15:46) = 12*61

Das auffälligste Ergebnis ist das Verhältis 1:3, das dem Kreisflächenverhältnis der beiden Tetraktyskreise entspricht. Der Faktor 61, der der ZS von TENET entspricht, trat bereits als ZS+FS der 8 verschiedenen Buchstaben in Erscheinung.

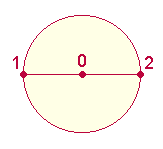
5. Entsprechend der zusammengesetzten Zahl 102 aus den numerierten Durchmesserpunkten 1–0–2 (s.o.) besteht die ZS des SATOR-Quadrats aus den Umkehrzahlen 102 und 201. Beide Zahlen sind die FS der Zahlen 1-16 und 1-23. Die Differenz 7 erklärt sich aus der Summe der Zahlen 1-3 = 6 und 1-4 = 10; 6+10 = 16; 3+4 = 7. Die Zahl 16, aus zweimal 3+5 bestehend, stellt die Radialelemente der beiden Tetraktyskreise dar. Sie geben jeweils das Kreisflächenverhältnis 1:3 wieder. Das FS:ZS-Verhältnis der Zahlen 1-16 ist 102:136 = 34*(3:4) und wiederholt so einerseits die Endzahl 3 und 4 und andererseits durch das interne Verhältnis 3:1 das Flächenverhältnis des äußeren zum hexagonalen Kreis.

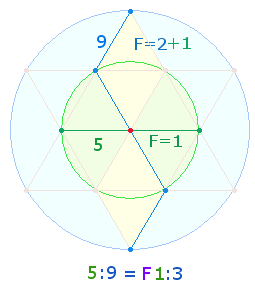
Die Zahl 23 gibt die Summe von Durchmesserelementen wieder, denen 7 Flächeneinheiten der beiden Kreise entsprechen: 5:9 = 1:3 und 5:4 = 1:2.

Die ZS 32 kommt zweimal durch PR und TN zustande. Das AK5 enthält 16 Linien. Die ZS+FS der Zahlen 1-16 und 1-23 beträgt 136+276 = 412+303 = 715 = 5*11*13 = FW 29.

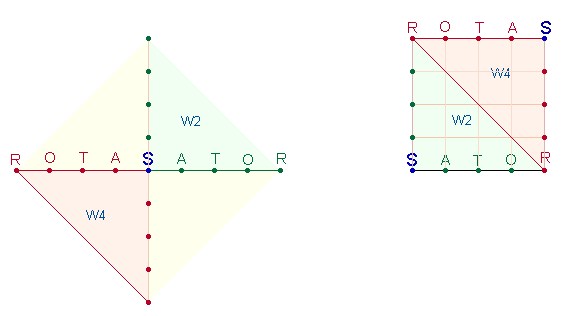
6. Die Zahlen 16 und 23 sind die Themen des äußeren Quadratrahmens: Die drei Mittelbuchstaben OTA/ATO sind konzentrisch dem ganzen Wort SATOR/ROTAS eingegliedert und haben die ZS 34, mit 4 multipliziert ist die ZS 136 die Summe der Zahlen 1-16. Wenn die ZS 69 einer Quadratseite ebenso mit 4 multipliziert, ist das Ergebnis 276 die Summe der zahlen 1-23.

Tatsächlich entspricht diese Sichtweise den drei geometrischen Figuren in der DR:

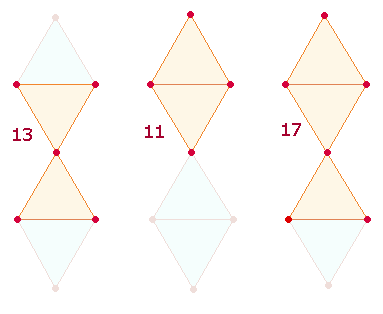
Das linke Doppeldreieck aus 13 Elementen ist die zentrale hexagonale Figur, die nach beiden Seiten zu zwei Rauten und zwei "Fischfiguren" erweitert wird. Letztere ergibt durch 2*17 = 34 die ZS der drei Mittelbuchstaben, 2*11+13 = 35 die ZS 17+18 der Buchstaben RS.

Eine Quadratseite verwirklicht so das oben bereits mehrfach genannte Prinzip des Teils zum Ganzen 3:5, das sich grundlegend herleitet von 3 Radialelementen und 5 Durchmesserelementen der Kreisachse.

Das Summenergebnis 136+276 = 412 ist in seinen Einzelziffern charakteristisch sowohl für das Quadrat an sich als auch für die konzentrische Ausdehnung von Quadraten. Denn jede der 4 Quadratseiten besteht aus 1 Maßeinheit und 2 Begrenzungspunkten. Jeder neue Quadrahmen enthält 8 mehr Punkte als der vorherige. Je zwei bilden mit einem Diagonalpunkt einen Winkel:

Erstellt: November 2005

Überarbeitet: Juli 2014, April 2016

Inhalt SQ