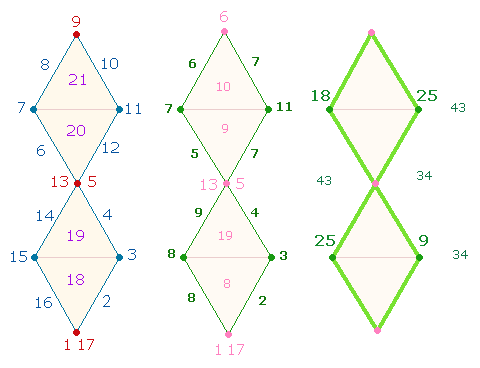
Die Zahlen 1-21
Ordnung der Zahlenwerte und
Faktorenwerte
in linearer Reihenfolge und in der
Doppelraute
|
Z.feld |
4 |
2 |
1 |
3 |
4 |
||||||||||||||||
|
Z.folge |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
10 |
|
FS |
|
9 |
18 |
|
|
|
|
|
25 |
25 |
|
||||||||||
|
6 |
27 |
44 |
50 |
38 |
|||||||||||||||||
|
44 |
|||||||||||||||||||||
1.
Die Zahlenfelder 2 1 3 bestehen aus 3*5 Einheiten, das Feld 4, zusammengefaßt zu einer Einheit aus 6 Zahlen, aus 2*3 Einheiten. Die mit den Feldern 1 und 4
bezeichnete Zahlengruppe und deren Faktorensumme (FS) 88 = 8*11 besteht aus 11 Zahlen und der Zahlensumme (ZS) 11*11, die anderen beiden Felder mit der FS 77 = 7*11 aus 10 Zahlen
und der ZS
10*11. Es herrscht
jeweils Teilbarkeit durch 11 und Parallelität zwischen FS und ZS, indem sie jeweils um einen Zähler
abnehmen (11-8, 10-7). Das FS:ZS-Verhältnis lautet 165:231 = 33*(5:7), das ZS+FS-Verhältnis 209:187 = 11*(19:17).
Die vier
Felder lassen sich in einem Kreis anordnen:
|
|
2.
Numeriert man einen Doppelrautenrahmen in
8-förmiger Umfahrung von 1-17 und besetzt darauf in Gegenrichtung die 4 Dreiecke mit den Zahlen 18-21, zeigen die 4*3 = 12 Rahmenelemente oder
Dachelemente (L+P+L) und die 9 vertikalen Elemente gewisse parallele
Faktorenverhältnisse zu der oben dargestellten Zahlenreihe, auch wenn es sich
um unterschiedliche Zahlen handelt:
|
|
Den FW auf der Zahlenskala 4+5 = 9 entsprechen die ersten 3
Rahmenelemente 2+3+4 = 9, dann folgen identisch für beide Reihen 6 7 8 mit der FW 5+7+6 = 18. Die nächsten 3
Faktorenwerte mit der Summe 25 sind von 10 11 12 gebildet, entsprechen
aber gleichzeitig der FS von 14 15 16. Die Zahlen 14 15 16 teilen mit den Zahlen 17
und 18 dieselbe FS 25.
|
Z.folge |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
FW |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
|
|
25 |
|
25 |
25 |
|||||
Die 4*3 Elemente haben in den
Umkehrzahlen 34+43 eine sinnfälltige Parallele.
Der
Vergleich der Zahlenanordnung zeigt, daß die FS 77 der 10 Zahlen der Kreismitte auf die 12 äußeren Dachelemente
übergegangen ist und die FS 88 der 9 vertikalen Zahlen den 11 Zahlen der Außenteile
des Kreises entspricht. Die Werte der 22:20 Zahlen sind:
|
22 |
ZS |
FS |
sm |
20 |
ZS |
FS |
sm |
|
Kr.in. |
110 |
77 |
187 |
Kr.au. |
121 |
88 |
209 |
|
DR au. |
108 |
77 |
185 |
DR in. |
123 |
88 |
211 |
|
|
218 |
176 |
372 |
|
244 |
176 |
420 |
|
372:420
= 12*(31:35) |
|||||||
3.
Rechnet man die Mittelpunktszahl 5 zur unteren Raute und
die 13 zur oberen, ergeben sich zwei gleiche Gesamt-ZS+FS:
|
|
ZS |
FS |
sm |
|
unt. Raute |
114 |
84 |
198 |
|
ob. Raute |
117 |
81 |
198 |
|
114:117 = 3*(38:39) |
|||
|
84:81 = 3*(28:27) |
|||
Die ZS und FS sind jeweils durch 3 teilbar.
4.
Die FS 3*25 = 75 = 5*15 und die restliche FS 6*15 legt die Vermutung nahe,
daß es noch eine weitere Einteilung der Zahlen 1-21 gibt:
|
Z.folge |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
10 |
Die FS 25 der Zahlen 10-12
wird konzentrisch erweitert um die FS 30 zu 55. Das FS:ZS-Verhältnis der 1+5+1 = 7 Zahlen, die die Punkteverteilung der Doppelraute (DR) wiedergeben, ist demnach 55:77 = 11*(5:7) = 132. Diese 7 von 21 Zahlen stellen also
genau ein Drittel des Gesamtverhältnisses 3*11*(5:7) dar.
Die nächsten beiden
konzentrischen Zahlen 2+20 mit ihren FW 2+9 fügen eine weitere Summe
22+11 hinzu, sodaß für diese 2+5+2 = 9 Zahlen zu den restlichen
12 Zahlen sich folgende
Verhältnisse ergeben:
|
|
FS |
ZS |
|
|
|
9 Z |
66 |
99 |
165 |
33*(2:3) |
|
12 Z |
99 |
132 |
231 |
33*(3:4) |
In der
konzentrischen Anordnung der ermittelten 9+12 Zahlen übernimmt die ZS+FS der 9 Zahlen
die gesamte FS und die der 12 Zahlen die gesamte ZS der 21 Zahlen.
Die FW teilen
sich folgendermaßen in 3*(25+30) = 3*5*(5:6) auf:
|
|
|
|
|
sm |
|
|
|
sm |
|
|
sm |
GS |
|
ZW |
10 |
11 |
12 |
33 |
14 |
15 |
16 |
45 |
17 |
18 |
35 |
113 |
|
FW |
7 |
11 |
7 |
25 |
9 |
8 |
8 |
25 |
17 |
8 |
25 |
75 |
|
sm |
|
|
|
58 |
|
|
|
70 |
|
|
60 |
188 |
|
ZW |
1 |
9 |
13 |
21 |
44 |
2 |
19 |
20 |
41 |
3 |
4 |
5 |
6 |
7 |
8 |
33 |
118 |
|
FW |
1 |
6 |
13 |
10 |
30 |
2 |
19 |
9 |
30 |
3 |
4 |
5 |
5 |
7 |
6 |
30 |
90 |
|
|
|
|
|
|
74 |
|
|
|
71 |
|
|
|
|
|
|
63 |
208 |
Faßt man
die drei durch 11 teilbaren ZS mit ihren FS
zusammen, erhält man das ZS+FS Verhältnis 195:201 = 3*(65:67).
5.
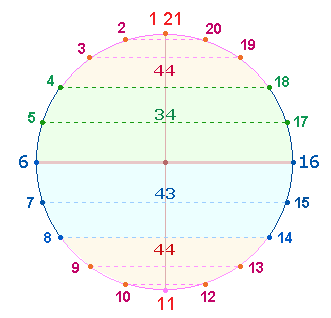
Auch in einer anderen Kreisdarstellung wird die
Parallelität sichtbar:
|
|
Man kann die FS und ZS der äußeren Teile zum
Mittelteil oder der oberen zur unteren Hälfte in Beziehung setzen:
|
|
|
FS |
ZS |
|
|
|
außen |
11 Z |
88 |
121 |
209 |
11*(8:11) |
|
Mitte |
10 Z |
77 |
110 |
187 |
33*(7:10) |
|
oben |
10 Z |
78 |
110 |
188 |
|
|
unten |
11 Z |
87 |
121 |
208 |
|
|
188:208 = 4*(47:52) |
|||||
Die ZS+FS 209
und 187 sind ZS in Catulls carmen 85.
1.
Die Zahlen des Achsenkreuzes bilden
Zahlenverhältnisse:
|
ZW |
1 21 |
11 |
6 |
16 |
55 |
|
|
FW |
1 |
5 |
11 |
8 |
10 |
35 |
|
35:55 = 5*(7:11) |
90 |
|||||
|
90:306 =
18*(5:17) |
||||||
Erstellt: 10.1 2005
Letzte Änderung: Juni 2011