Die Zahlen 14-18 und 12-21
Da ich mittlerweile die Zusammenhänge besser
erkenne, seien sie hier dargestellt:
1. Wenn man die Einerstellen der
Zahlen 14 und 18 jeweils addiert, erhält man mit 5 und 9 die Durchmesserelemente des
Doppelkreises, der den Tetraktysstern enthält. Durch die beiden Zahlen wird
also eine Entwicklung und Erweiterung des Hexagons zum Tetraktysstern
angezeigt. Die Produktzahlen 14*18 ergeben ebenso wie 12*21 die Zahl 252. Letztere kann man wieder auf die
DM-Elemente
des Doppelkreises beziehen, indem zu den 5 DM-Elementen des inneren Kreises symmetrisch je zwei weitere
hinzukommen. Die Fläche des kleineren Kreises verhält sich zum Kreisring des
größeren 1:2
und zum ganzen größeren Kreis 1:3. Als zweistellige Zahlen addiert ergeben die
beiden Verhältniszahlen 25. Diese Zahl kommt zweimal als Faktorensumme (FS)
zustande, wenn man die FW von 14+15+16 und 17+18 addiert: 9+8+8 = 25; 17+8
= 25. Addiert man ZS+FS, ist das Verhältnis beider
Zahlengruppen 70:60 = 10*(7:6). Die Zahlen 7 und 6 lassen sich auf die 7 Punkte des Hexagons und 6 Punkte der äußeren Kreislinie
beziehen.
2. Wenn man die 5 Zahlen von 14-18 als DM-Elemente des Kreises
ansieht, besetzen die Zahlen 14, 18 und 16 zwei Kreislinienpunkte und den Mittelpunkt und 15 und 17 zwei Radiallinien. Die FS der
Punkte- wie auch der Liniennumerierung ist jeweils 25.
3. Die Zahl 25 korrespondiert mit 10 durch das Produkt 2*5, das den FW 7 bildet. Den FW 10 erhält man durch 5*5 = 25. Die Rechnung (5+5)+(5*5) ergibt die ZS 35 und die FS 17. Die Zahl 17 ist die untere Konstitutive der
Zahl 35. Die Addition 35+17 führt zur Umkehrzahl 52.
Die Zahl 17 kommt auch zustande durch die FW 7+10 von 12
und 21. Sie ist auch vertreten durch die
7
Punkte und 10
Linien der Doppelraute.
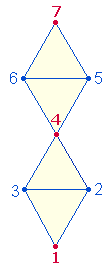
4. Die Zahlen 5+2 beziehen sich besonders auf die 5 Punkte eines Doppeldreiecks des
Hexagons und 2
weitere Punkte, die aus dem Doppeldreieck eine Doppelraute machen. Betrachtet
man die 3+2 Radialelemente des Doppelkreises
als 32, zeigt sich eine Beziehung der
Zahlen 5 und 2: Die 5. Potenz von 2 ist 32. Die konzentrischen Zahlenpaare 14+18 und 15+17 ergeben die Komplementärzahl 32.
5. Die FS
der Zahlen 12 und 13 ist 7+13=20, also 2*5 je Zahl. Das Verhältnis ZS:FS ist 25:20 = 5*(5:4). Der gemensame Faktor 5 bezieht
sich auf die 5 DM-Elemente des inneren Kreises, 5+4 = 9 auf die DM-Elemente des inneren
Kreises + äußeren Kreisrings.
Auf die Flächen des Doppelkreises bezogen bedeuten 5:9 DM-Elemente das Verhältnis 1:3. Die Zahlen 13 und 12 bedeuten 13 Punkte und 12 Dreiecke des Tetraktyssterns.
6. Die Zahlen 12-18 mit der Unterteilung 2+5 haben – gleichsam motivgleich –
den durchschnittlichen FW 2*5. Das (externe) Verhältnis von
FS:ZS ist 70:105 = 7*5*(2:3). Das interne Verhältnis von
FS:Rest-ZW ist 70:35 = 7*5*(2:1). Externes und internes Verhältnis
beziehen sich jeweils auf den äußeren Kreisring und den inneren
Kreis: 2:3 Radialelemente und 2:1 Flächengröße.
Setzt man analog zu
den Radialelementen die Punkteverteilung der DR in Flächenverhältnisse um,
bedeuten 7 und 5 Punkte die Flächengrößen 3 und 1. Die Zahlen 12-18 können also besonders auf die
Doppelraute bezogen werden und ergeben die beiden Verhältnisse 3:1 und 2:1 (internes Verhältnis), die
addiert wieder zur Zahl 7
zurückführen.
7. Wenn wir zu den 2+5 Zahlen von 12-18 noch 19 und 20 hinzunehmen, sind wir bei 2+5+2 DM-Elementen des Tetraktyssterns
angelangt. Die ZS ist 9*16 =
144
= 12*12, die FS 98. Die Zahl 144 selbst bezeichnet die 9
DM-Elemente treffend durch den Mittelpunkt und je 4 Symmetrieelemente. Als
Quadratzahl stellt sie die 2*6 Kreislinienpunkte und 2*6 Dreiecke sowie das
Flächenverhältnis 1:2 dar. Die Zahl 98 ist der Komplementärwert zu 12 und steht somit in sinnvoller
Beziehung zur ZS (12*12). In der Aufteilung 9+8 und der Produktaufteilung 7*14 verweist sie vermutlich auf die 8-förmige
Numerierung und 21 Elemente der DR, aber auch auf
die 3*7 Elemente des Tetraktysrahmens. Die Addition 144+98 ergibt die
Umkehrzahl 242,
die zusammen mit der Umkehrzahl 252 den ZW der 6 Namen der Kapitolinischen Trias bildet. Möglicherweise besteht
ein direkter Zusammenhang zwischen beidem.
8. Die Buchstaben O-S verdanken ihre
Bedeutung dem Produkt 14*18, das wie 12*21 die Zahl 252 ergibt. Sie bilden
somit die innere Mitte der Zahlen 12 bis 21 und eine Hälfte von 10
Radialelementen des Doppelkreises. Diese eingeschobene Zahlengruppe unterteilt
die 10 Zahlen in die Folge 2+5+3. Die Faktoren 11*23 = 253 drücken – in
versetzter Reihenfolge – die Flächenverhältnisse des Doppelkreises 1:2 und 1:3
aus.
9. Die Zahlen 14-18 ergeben die FS 50 und ZS 80, zusammen 130. Das Verhältnis ist 10*(5:8). Die übrigen 5 Zahlen bilden mit der FS 58 und der ZS 85 Umkehrwerte, deren Summe 11*13 = 143 ist. Die beiden Gruppen von
Radialelementen verhalten sich also zu einander 13*(10:11) = 13*21,
das ist die Umkehrung von 12+13 in Produktform.
Die Zahlen 5 und 8, die in beiden Zahlengruppen
vorkommen, bezeichnen die beiden Flächenverhältnisse 1:2 und 1:3 durch 5 Radialelemente: 5 = 3:2,
8 = 3:5. Addiert ergeben die Flächenverhältnisse
die Zahl 7, die Radialelemente die Zahl 13.
Die Zahlen 5 und 8 zeigen ihre heilsgeschichtliche
Bedeutung in den 5+8 Buchstaben der Namen IESVS CHRISTVS, die ich im Zusammenhang mit dem SATOR-Quadrat behandelt habe. Die ZS+FS der beiden Namen ist 182+112 = 294, die der Zahlen 12-21 273. Das Verhältnis der beiden Summen ist 21*(14:13).
10. Die 5 Zahlen von 14-18 haben in
der bisherigen Untersuchung die wichtigtsten Abfolgen von Punkten und Linien im
Tetraktysstern gezeigt:
–
die
5
DM-Elemente des einfachen Kreises und Aufteilung der 10 Zahlen in 2*5 Radialelemente;
–
die
Zahl 7
ist vertreten in den 7
Punkten a) des Hexagons, b) der Doppelraute, c) den 4P+3L einer Tetraktysseite;
–
die
9
DM-Elemente des Doppelkreises in der Abfolge 2-5-2.
–
Die
Sondergruppe von 5
Zahlen legt auch die Aufteilung in 2*5 und 2*3 Radialelemente des Doppelkreises und des inneren Kreises nahe. Die
aufgezeigte Abfolge 2-5-3 ist allerdings bei einem systematischen Vergleich
aller Zahlenabfolgen hinter einem linearen und konzentrischen Ablauf 5-5 und 3-3 zurückzustellen.
Die folgende Übersicht versucht, in den 5 Abfolgen eine sinnvolle Ordnung
sichtbar zu machen. Zu diesem Zweck werden die jeweiligen ZW und FW der Punkte
und Linien ermittelt. Punkte werden rot, Linien blau dargestellt:
|
5 |
|
|
14 |
15 |
16 |
17 |
18 |
|
|
|
|
7 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
|
|
9 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
5-5 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
3-3 |
|
|
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
Punkte |
Sm. |
Linien |
Sm. |
GsSm. |
||
|
Z |
ZS |
FS |
|
ZS |
FS |
|
|
|
5 |
48 |
25 |
73 |
32 |
25 |
57 |
130 |
|
7 |
60 |
32 |
92 |
45 |
38 |
83 |
175 |
|
9 |
80 |
41 |
121 |
64 |
57 |
121 |
242 |
|
Sm. |
188 |
98 |
286 |
141 |
120 |
261 |
547 |
|
5-5 |
99 |
70 |
169 |
66 |
38 |
104 |
273 |
|
3-3 |
66 |
53 |
119 |
33 |
16 |
49 |
168 |
|
Sm. |
165 |
123 |
288 |
99 |
54 |
153 |
441 |
|
GsSm. |
353 |
221 |
574 |
240 |
174 |
414 |
988 |
|
ZS:353+240=593 |
FS:221+174=395 |
||||||
Entsprechend den Umkehrzahlen 12-21 zeigen auch die Tabellenwerte einige bemerkenswerte
Umkehrungen:
–
Die
Gesamtsumme der 3 Zahleneinheiten 5-7-9 und die Summe aller Punktewerte haben die Umkehrwerte 547 und 574. Die Zahlen 5 und 4 bezeichnen die 5 DM-Elemente des inneren Kreises +
2*2 Elemente für die konzentrische
Kreiserweiterung. Die 7 Elemente einer Tetraktysseite werden durch die
DM-Elemente des Doppelkreises ermöglicht.
–
Die
Gesamtsumme der beiden Radialeinheiten 5-5 und 3-3 korrespondiert mit der Summe aller Linienwerte durch die Umkehrzahlen
441
und 414.
Beide Zahlen geben die Symmetrieteile der 9 DM-Elemente des Doppelkreises wieder. Die Differenz
zwischen den Umkehrzahlen ist jeweils 27 = 3*9.
–
In
den Umkehrzahlen 395 und 593 sind die DM- und Radialelemente des Doppelkreises
enthalten.
–
Entsprechend
den 7
Punkten des Hexagons und den 13 Punkten des Tetraktyssterns sind die Punkte- und
Liniensummen der Radialelementen 3-3 und 5-5 jeweils durch 7 bzw. 13 teilbar: 169:104 = 13*(13:8); 119:49 = 7*(17:7). Die Summen 273 und 168 haben das Verhältnis 21*(13:8). Das Zahlenverhältnis bezeichnet
die 13 Elemente des Doppeldreiecks, das
durch weitere 8
Elemente zur Doppelraute erweitert wird. Auf die Fläche des inneren Kreises und
des äußeren Flächenrings übertragen ergibt sich das Verhältnis 2:1 und entspricht damit der Summe
beider Verhältniszahlen.
11. Die 10 Zahlen von 12-21 werden durch die 5 Zahlenreihen auf 37 vermehrt. Die Gesamtsumme der ZW+FW 988 – deren Einzelziffern in genauer
Reihenfolge mit den FW der Zahlen 14,15,16 übereinstimmen– ist wie die Ausgangssumme 273 durch 13 teilbar: 4*13*19= 13*76. Im Produkt 13*76 begegnet sich die Zahl 13 – wegen 7+6=13 – gewissermaßen selbst.
Der Zuwachs der
Gesamtsumme zur Ausgangssumme 273 ist (76-21)*13 = 55*13 = 715.
12.
Bemerkenswert
sind die Differenzen der ZW und FW:
|
|
|
|
|
FW |
|
ZW |
593-165 |
428 |
4*107 |
111 |
|
FW |
395-108 |
287 |
7*41 |
48 |
|
|
|
|
|
159 |
Beide
Differenzprodukte enthalten die Zahlen 1-4-7, die die vertikale Numerierung der DR bilden:
|
|
Addiert man die
Einzelziffern der beiden Produkte und liest 107 als 10+7, erhält man mit 7+4+1 = 12 und 4+10+7 = 21 die Ausgangssituation der 10 Zahlen.
Die beiden Addition
verdeutlichen beispielhaft die Weiterentwicklung des Dezimalsystems von der
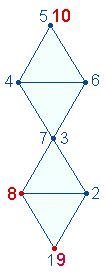
Zahl 7 zur Zahl 10, wenn die Doppelraute 8-förmig
numeriert wird und nach Vereinigung der beiden DR-Spitzen die 10. neben der 5.Position besetzt wird:
|
|
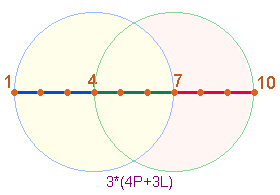
Das folgende Streckenmodell, das
aus 10 Punkten und 9 Linien besteht, macht deutlich,
daß die Punkte 4 und 7 die Skala 1 bis 10 in 3 gleiche Abschnitte teilt: Je 4 Punkte begrenzen 3 Maßeinheiten. Die Erweiterung von
1-7 zu 10 Punktekn bedeutet also einen Zuwachs um ein Drittel. Das Verhältnis
1-7:7-10 ist daher 2:1:
|
|
Erstellt: September 2005