zurück

Die Zahl 35 (II)

X. Die Umkehrzahlen 25 und 52

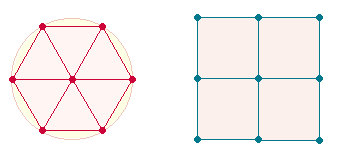
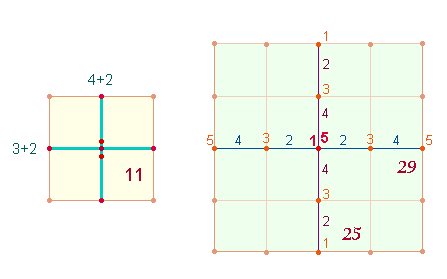
1. In geometrischer Darstellungsform zeigt eine Quadratzahl vollkommene Spiegelbildlichkeit und Gleichheit. Sowohl das Hexagon (7P+6F+12L) als auch das Quadrat des Achsenkreuzes 2 (9P+4F+12L) bestehen aus 25 Elementen:

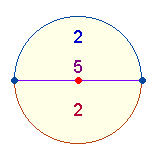
Ein Hexagon wird gewöhnlich in einen Kreis hinein konstruiert. Ein Kreis besteht aus 3 Elementen: MP, Kreislinie und Fläche. Daher kann man den 25 Elementen noch 3 – oder bei gemeinsamem MP – 2 Elemente hinzuzählen. Die Zahl 27 ist die einzige konstitutive Zahl, die mit ihrer zweiten deren Umkehrung bewirkt: 25+27 = 52.

Der gesamte Tetraktysstern besteht aus 25+24 = 49 Elementen. Fügt man den 24 Elementen des äußeren Flächenrings noch Kreislinie und Fläche hinzu, erhält man für das Flächenverhältnis 1:3 die Werte (25+2):(25+2+24+2) = 27:53. Die Summe der beiden Verhältniszahlen ist 80, worin die Zusammensetzung 3+5 erkennbar ist.

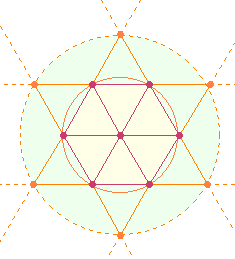
Für die Weiterkonstruktion des Hexagons zum Tetraktysstern ist ein Kreisbogen entbehrlich. Er ist gewissermaßen ein freiwilliger Zusatz. Es ist daher sinnvoll, die Flächenverhältnisse beider Kreise zu einander vom äußeren Kreis her zu definieren. Man wird also zu den 24 äußeren Elementen noch 3 weitere zu insgesamt 27 hinzufügen: äußeren und inneren Kreisbogen und die Fläche zwischen beiden Kreisbögen:

Das Verhältnis des inneren Kreises zum gesamten äußeren ist nun 25:52. Die Faktorenteilungen der Zahlen 2552 und sind auf 9 bzw. 5 Durchmesserelemente anwendbar:

2552 = 8*11*|29 (48 E); 5225 = 11*|19*|25 (55 E), zus. 103 Elemente.

2. Die beiden Zahlen 2552 und 5225 enthalten 2 numerierte (29, 25) und 3 unnumerierte Teilungszahlen (8*11, 11, 19). Die unnumerierte Teilungszahlen sind doppelt zu zählen, einmal mit 1 und einmal mit 2 Mittelpunkten. Der Teilungsfaktor 11 in der Zahl 5225 bezieht sich auf 5 Durchmesserelemente. 2 Einfach- und 3 Doppelzählungen nehmen also 8 DM-Linien in Anspruch.

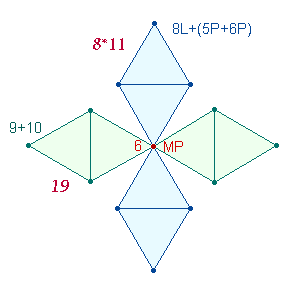
Will man eine ausgewogene Zuordnung der 8 Zählungen, würde man die unnumerierten Teilungszahlen auf ein Doppelrautenkreuz und auf das AK2 und man die numerierten Teilungszahlen auf zwei Achsen des AK3 anwenden,:

3. Man kann die 8 Zählungen nach Punkten, Linien und Mittelpunkten trennen. Da sie außerdem allesamt auf den Tetraktysstern bezogen werden können, sind auch die Werte des äußeren Ringes und des inneren Kreises von Bedeutung:

	Teiler	P	L	MP	AußenE	Innen-E
2552	8*11	8	8	3	8	11
	29	16	12	1	18	11
5225	11	4	4	3	–	11
	19	8	8	3	8	11
	25	8	12	5	6	19
		44	44	15	40	63

4. Die Zahl 35 aus 4*31 erhalten wir durch folgende ZW-FW-Verrechnung der P-, L- und MP-Ergebnisse:

	ZW	FW	Sm.FW
	44	15
	44	15
	15	8
Sm.	103	38
FW	103	21	124
124=4*31>35

5. Von den 15 MP stammen 3*3 =9 aus den Doppelzählung der Teilerwerte 8*11, 11, 19 und 6 von den numerierten Ergebnissen 29 und 25. Die Zahl 9 läßt sich am auf die 3*3 Punkte der 3 Hexagonachsen, die Zahl 6 auf die 3*2 Radiallinien beziehen, insbesondere aber auch auf die 3*2 = 6 Durchmesserlinien des Tetraktyssterns mit ihren jeweils 9 Elementen und die 2 Einzelzählungen auf 2 Achsen des AK3 oder AK5. Die Produktaufteilung 3*5 = 15 verweist gleichzeitig auf die 3 und 5 Radialelemente des inneren und ganzen äußeren Kreises.

6. Wenn man die beiden trinitarischen Verhältnisse 1:2 und 1:(1+2) auf Elemente des inneren Kreises k1 und des äußeren Kreises k2 bezieht, um eine Berechnung durchführen zu können, lautet die Formel 3k1+2k2, also 3*1+2*2 = 7 Flächeneinheiten. Die 3+2 Radialelemente des inneren und äußeren Kreise heißt demnach die Rechnung 3*3+2*2 = 9+4 = 13. Da ein Kreis zwei Radien besitzt, ist die Verdoppelung der Zahl 13 auf 26 sinnvoll. In der Zahl 26 treten uns wieder die 2 einfachen und 2*3 = 6 Doppelzählungen der Durchmesserlinien entgegen, aber auch die 26 Elemente des Oktaeders.

Wenn man in gleicher Weise mit den tabellarischen Werten 63 und 40 für den inneren und äußeren Kreis verfährt, ergibt sich 3*63 = 189 + 2*40 = 80, zusammen 269 (Primzahl). In diesem Gesamtergebnis tauchen die oben behandelten Einzelzahlen wieder auf.

Wenn man die Zahl 269 in ihre 2-stelligen Kombinationen aufteilt, erhält man 26+29+69 = 124 = 4*31>35. Die dazugehörigen FW sind 15+29+26 = 70>14. Das Verhältnis 35:14 = 7*(5+2) verweist auf die 5+2 Punkte der Doppelraute und die 2*7 Elemente der Kreishälften:

Multipliziert und addiert man schließlich die Einerzahlen, erhält man 2*6*9= 108 + 17 = 125 = 5³.

Erstellt: April 2005

Inhalt