Zyklische Zahlen
(II)
B. Definition und
Einordnung der Zahlen 1, 2 u.5
I.Einleitung
IV.
Ordnungsstrukturen in Tetraktysstern und Doppelkreis
V. Primzahlen
zwischen 1 und 100
VI.
Primzahlen zwischen 1 und 1000
VII.
Primzahlen zwischen 1 und 100.000
Wie ich im vorhergehenden Kapitel darlegte, haben alle Primzahlen
zyklische Struktur. Ausgenommen sind die Zahlen 1, 2 und 5. Wie fügen sich
diese 3 Zahlen in die Zahl der übrigen Primzahlen ein, wenn man davon ausgeht,
daß das System der Zahlen ein einziges Ordnungs- und Sinngefüge darstellt? In
diesem Kapitel werde ich versuchen, Antworten darauf unter ontologischen
Gesichtspunkten zu geben. Als grundlegender Maßstab und Bezugspunkt wird dabei
der Tetraktysstern im Doppelkreis in Erscheinung treten.
II.
Definition der Zahl 1
1.
Man
hat sich in der offiziellen Mathematik darauf verständigt, die Zahl 1 nicht zu
den Primzahlen zu rechnen, da sonst bei weiteren Definitionen stets auf die
Zahl 1 als Ausnahme verwiesen werden müßte. Eine Übersicht über das Problem ist
bei Wikedia zu finden. Es sind also weniger prinzipielle als vielmehr
praktische Gründe, die Zahl 1 von den Primzahlen auszuschließen.
2.
Unter
anderem Gesichtspunkt ist die Zahl 1 als Ursprung aller übrigen Zahlen zu
sehen. In ihrem Wesen ist sie identisch mit sich selbst. Sie wird in den weiteren
Ausführungen immer zu den Primzahlen gerechnet.
III.
Gesetz und Gesetzgeber
1.
Es
ist zweifellos Aufgabe der Mathematik, nach legitimen Prinzipien Gesetze zu
formulieren. Aber wer ist der Gesetzgeber der Mathematik? Sicherlich nicht der
Mensch. Es stellt sich allerdings die Frage, welchen Nutzen es für die
Mathematik hätte, einen metaphysischen Urheber in mathematisches Denken mit
einzubeziehen. Eine kurzgefaßte und thesenartige Antwort soll nicht in Form von
Beweisgründen, sondern von der Perspektive einer göttlichen Erstursache von
allem gegeben werden:
2.
Die
Ordnung, die Gott der Schöpfung gegeben hat, steht im Einklang mit seinem
Wesen. Menschlicher Erkenntnis sind Grenzen gesetzt. Mathematisches
Unendlichkeitsdenken muß sich des wesentlichen Unterschieds zum Begriff der
Unendlichkeit Gottes bewußt bleiben. So wie der Mensch nicht Ursprung seiner
selbst ist, sondern sich als Gegebenheit erfährt, so sind die Ordnungen des Geschaffenen Gegebenheiten, erforschbar, aber nicht
ergründbar. Die Weisheit Gottes und seiner Schöpfung ist rational, nicht irrational. Mathematik,
die die Unendlichkeit Gottes mitbedenkt, hütet sich gleichermaßen vor
Irrationalität und falscher Rationalität. Sie verzichtet z.B. auf die
fruchtlose Spekulation, ob es unendlich viele Primzahlzwillinge gibt. Vielmehr
wird sie im endlichen Bereich versuchen, weise Ordnungen ausfindig zu machen.
Der gläubige Mathematiker betrachtet seine Wissenschaft nicht als ein Mittel
autonomer Selbstbehauptung, er erkundet den Spielraum ihrer
Wirkungsmöglichkeiten im Bewußtsein der ihr gesteckten Grenzen.
Ich selbst glaube an
Ordnungsstrukturen der Zahlen, die das Wesen des einen Gottes in drei Personen
widerspiegeln.
IV.
Ordnungsstrukturen in Tetraktysstern und Doppelkreis
1.
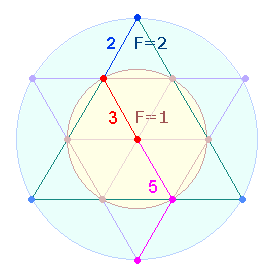
Die
Zahl 1 bildet keinen Dezimalbruch, die
Zahlen 2 und 5 keine Periode. Diese 3 Zahlen,
die somit nicht zu den zyklischen Primzahlen gehören, übernehmen zwei
konstitutive Aufgaben für das Dezimalsystem im Doppelkreis des Tetraktyssterns:
–
Die
Zahlen 1 und 2 stellen die Flächengrößen des
inneren und des äußeren Kreisringes dar.
– Der Zahl 5 entsprechen 3 Radialelemente des inneren
Kreises und 2
Radialelemente des äußeren Kreisringes:
|
|
2.
Die
Zahlen 1,
2 und 5 können auch beiden Kategorien von
Fläche (F) und Radialelementen (RE) zur Verfügung stehen. Demnach ist nicht nur
das Verhältnis von innerem Kreis und äußerem Kreisring (KR), sondern auch von
innerem Kreis (inK) und ganzem äußeren Kreis (äuK)zu berücksichtigen. Die
Radialelemente repräsentieren Die Flächenverhältnisse werden den
Durchmesserelementen (DME) in einfacher und von den Radialelementen sowohl in
einfacher als auch doppelter Zählung repräsentiert:
|
|
inK |
KR |
Sm. |
inK |
äuK |
Sm. |
Gs.Sm. |
|
F |
1 |
2 |
3 |
1 |
3 |
4 |
7 |
|
RE |
3 |
2 |
5 |
3 |
5 |
8 |
13 |
|
DME |
5 |
4 |
9 |
5 |
9 |
14 |
23 |
|
Sm. |
9 |
8 |
17 |
9 |
17 |
26 |
43 |
|
RE |
3 |
2 |
5 |
3 |
5 |
8 |
13 |
|
GsSm |
12 |
10 |
22 |
12 |
22 |
34 |
56 |
|
24:32 = 8*(3:4) |
|||||||
Die Fläche des inneren Kreises zum
äußeren Kreisring verhält sich also 1:2, die entsprechenden Radialelemente 3:2. Weiterhin ergibt sich aus dem
Flächenverhältnis 1:3 des inneren Kreises und des ganzen äußeren Kreises für
die Radialelemente das Verhältnis 3:5. Addiert man die Verhältniszahlen
3+2 = 5 und 3+5 = 8, erhält man das Verhältnis 5:8.
Dem (einfach gezählten) Verhältnis
3:5
der Radialverhältnisse schließlich entspricht das Verhältnis 5:9 der DM-Elemente. Die 9 zyklischen Zahlen erster Ordnung
zwischen 1 und 100: 7, 17, 19, 23, 29, 47, 59, 61, 97 ergeben die Summe 359.
3.
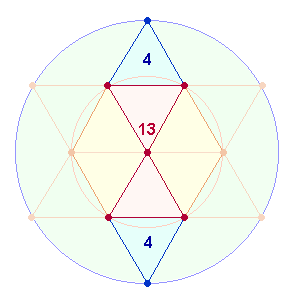
Die
Addition 3+5
und 5+8
führt zum Verhältnis 8:13. Dieses Verhältnis bezieht sich auf die gesamten 21 Elemente der Doppelraute. Davon
entfallen 13 auf die Flächengröße 1 des inneren Kreises und 2*4=8 auf den äußeren Flächenring von der
Flächengröße 2:
|
|
Wendet man die Zahlen der 3
Verhältnisse auf die Flächengrößen 1 und 2 an, erhält die innere Kreisfläche (3+3)+(3+6)+13 = 28 und der äußere Kreisring 2+(2+2)+8 = 14. Damit ist das Verhältnis 14*(2:1) von innerem Kreis und äußerem Kreisring umgekehrt
proportional zu ihren Flächen.
4.
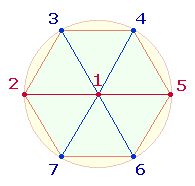
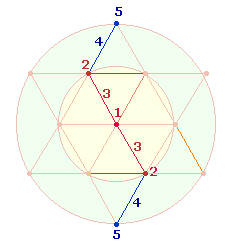
Die
Zahlen 1,
2 und 5 besetzen die 3 Punkte der Mittelachse eines
Hexagons, wenn man die 6
Punkte auf der Kreislinie reihum numeriert:
|
|
Sie erinnern auch an die
Grundkonstruktion des Goldenen Schnitts: 2²+1² = 5.
V.
Primzahlen zwischen 1 und 100
1.
Die
Verhältnisse 3:5, 5:8 und 8:13 zwischen zyklischen Zahlen (1.
Ordnung) und den übrigen Primzahlen sind bereits zwischen 1 und 71 vorhanden, wenn man die Zahlen 1,
2, 5 den
"übrigen" Primzahlen zuordnet:
|
Vh. |
|
|
|
|
|
|
|
|
|
|
|
|
|
zykZ |
übPZ |
|
5 |
7 |
17 |
19 |
23 |
29 |
|
|
|
|
|
|
|
|
95 |
|
|
8 |
1 |
2 |
3 |
5 |
11 |
13 |
31 |
37 |
|
|
|
|
|
|
103 |
|
6 |
7 |
17 |
19 |
23 |
29 |
47 |
|
|
|
|
|
|
|
142 |
|
|
10 |
1 |
2 |
3 |
5 |
11 |
13 |
31 |
37 |
41 |
43 |
|
|
|
|
187 |
|
8 |
7 |
17 |
19 |
23 |
29 |
47 |
59 |
61 |
|
|
|
|
|
262 |
|
|
13 |
1 |
2 |
3 |
5 |
11 |
13 |
31 |
37 |
41 |
43 |
53 |
67 |
71 |
|
378 |
|
|
499 |
668 |
|||||||||||||
|
1167 |
|||||||||||||||
Bemerkenswert ist die doppelte Zählung der
Radialelemente 2*(3:5) der
mittleren beiden Spalten. Die Summe der beiden Reihen 142+187 beträgt 329, das
Siebenfache der zyklischen Zahl 47. Die
Zahl 47 bildet die Mitte der 21 Primzahlen zwischen 11 und 97.
2.
Die
Zahl 13 spielt
eine bedeutende Rolle in verschiedenen Summen von Primzahlen. Zwischen 1 und 100 gibt es 26 Primzahlen. Die Zahl 26 ist als doppelte Zählung des Radialverhältnisses 5:8 zu verstehen.
Die Summe der 9 zyklischen Zahlen 1. Ordnung beträgt 359 (7,17,19,23,29,47,59,61,97), die der 8 zyklischen Zahlen 2. Ordnung 400 (3,13,31,43,67,71,83,89), und die übrigen 6
(zyklischen)
Primzahlen 294 (11,37,41,53,73,79). Als
Gesamtsumme erhält man 1053 = 81*13. Es zeigt sich nun, daß man die
Basiszahlen 1, 2, 5
so auf die drei Teilsummen verteilen kann, daß jede durch 13 teilbar ist, von allen dreien
aber nur zwei.
Fügt man 5 zu 359 oder 294, erhält man 28*13 oder 23*13, addiert man 1+2 zu 400, ergibt sich 31*13. Die Zahlen 1, 2 und 5 sind also nicht auf eine der 3
Gruppen festgelegt, sondern dienen einmal hier und einmal dort der Herstellung
von harmonisch-proportionalen Verhältnissen.
VI.
Primzahlen zwischen 1 und 1000
1.
Den 13+13 Primzahlen von 1-100 entsprechen 13*13 von 1-1000. Davon entfallen 60 auf zyklische Zahlen erster
Ordnung, 54
zweiter Ordnung und 52 der übrigen Ordnungen. Die bekannten 3 nicht-zyklischen Zahlen fügen
sich komplementär allen 3 Gruppen
ein: Zählt man sie zu 52, bilden die Zahlen 55+54 die Konstitutiven der Zahl 109, fügt man sie zu 54 hinzu, erhält man durch 3-Teilung
die Konstitutiven 19:20 als Verhältnis, addiert man sie zu 60, erhält man das Verhältnis 9*(7:6) und zusammen mit 52 das Verhältnis 13*(9:4).
Die
Zahlen 60:54:52 schließlich lassen sich durch
Teilung auf Konstitutivzahlen zurückführen: 6*(10:9),
2*(27:26).
2.
Auch
das Additionsergebnis 76128
aller 169 Primzahlen ist durch 13 teilbar. Eine gemeinsame
Teilungszahl von 8*13 = 104 ergibt sich, wenn man die Summe der 60 zyklischen Zahlen 1. Ordnung mit
der Summe der übrigen 109
Zahlen vergleicht: 26936: 49192 = 104* (259:473). Bei der Summe der zyklischen Zahlen 2. Ordnung 25048 und solcher höherer Ordnung 24136 tritt wiederum das
Verteilungsprinzip des Basiszahlen 1,2,5 in Erscheinung. Fügt man der
einen Summe die Zahl 3, der anderen die Zahl 5 hinzu, sind beide durch 13
teilbar: 25051 = 13*41*47, 24141
= 13*3*619.
VII.
Primzahlen zwischen 1 und 100.000
1.
Die
Anzahl der zyklischen Zahlen 1., 2. und höherer Ordnung ist 3617, 2684 und 3289, zusammen 9590. Die Zahlen 9-(5-9) sind auf die DM-Elemente des
Tetraktyssterns beziehbar und spiegeln die Flächenverhältnisse (1+2)+(1+3) = 7 wider. Die Faktoren 7*137 weisen denn auch auf die
Flächenverhältnisse 7 und die Punktezahlen 13+7 des ganzen Tetraktyssterns mit den Flächenentsprechungen 3+1 = 4 hin, der FW 144 auf den Mittelpunkt + symmetrische 4+4 DM- bzw. Radialelemente.
2.
Die
Zahlen 2684
und 3289
sind durch 11 teilbar, die Summe beider 5973 ist aufteilbar in das Produkt 33*181. Fügt man der Primzahl
3617
die 3 Grundzahlen 1,2,5 hinzu, ergibt die Summe 3620 das Produkt 20*181.
Die
Addition beider Summen zum Produkt 53*181 zeigt Übereinstimmung mit der Addition der beiden
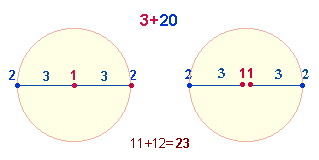
Zahlhälften 36+17. Diese
beiden Zahlen sind Faktorenwerte der dreistelligen
Umkehrzahlen 20-3 und 3-20, die sich aus den beiden
Numerierungsweisen einer Kreisachse ergeben:
|
|
3.
Das
genaue Häufigkeitsverhältnis von zyklischen Zahlen 1. Ordnung (Z1) und höherer Ordnung
(Zn) hängt davon ab, wie man die 3 freien Zahlen auf die beiden Gruppen
verteilt. Insgesamt gibt es 5 Möglichkeiten: Z1-Zn = 0-3, 1-2, 2-1, 3-0, 0-0. Die letzte Möglichkeit klammert die drei Zahlen aus.
Mit Ausnahme des Verhältnisses 3:5 treten die folgenden 4 Verhältnisse am häufigsten auf:
|
|
|
0-3 |
1-2 |
2-1 |
3-0 |
0-0 |
Sm. |
|
3:5 |
0,6 |
– |
2 |
– |
4 |
2 |
8 |
|
5:8 |
0,625 |
7 |
9 |
8 |
12 |
9 |
45 |
|
8:13 |
0,614 |
14 |
13 |
14 |
7 |
8 |
56 |
|
11:18 |
0,611 |
7 |
23 |
16 |
12 |
22 |
80 |
|
14:23 |
0,608 |
5 |
7 |
6 |
10 |
11 |
39 |
Die acht 3:5 Verhältnisse treten zwischen 44029 und 44533 auf,
haben also gewissermaßen in 4+4 eine
symmetrische Entsprechung. Die 16 Zahlen befinden sich in einer
Gruppe von 47 Zahlen,
die durch die Punkte 16-15-(16) auf einem Kreisbogen als mit
einander verwandt dargestellt werden können. Die Differenz der beiden Zahlen
ist 504 = 2*252. Die Zahl 252 ist zerlegbar in die Umkehrzahlen 12*21, die sich wiederum wie 4:7
verhalten. Die 24. Zahl dieser Gruppe als
symmetrischer Mittelpunkt ist 44263 und hat zur ersten und
letzten Zahl die Differenz von 234 und 270 = 18*(13:15).
Das am häufigsten auftretende
Verhältnis 11:18 läßt sich auf die Numerierung der
Durchmesserelemente des Doppelkreises zurückführen und entspricht einem
Flächenverhältnis von 1:2:
|
|
Das Verhältnis 14:23 ist zu verstehen als Summe der
DM-Elemente (5+9):(9+5+9) und entspricht einem Flächenverhältnis von 4:7.
Erstellt: Januar 2006