zurück

VESTA = ES TAV in 9 Versen der AENEIS

f) 36 Buchstaben im Achsenkreuz und Quadrat

Einführung

1. In der Aeneis des Dichters Vergil finden sich 9 Verse, die das Wort ES – Du bist enthalten und in Bezug zum Namen VESTA stehen. Zwei dieser Verse haben jeweils denselben Zahlenwert (ZW) 497 = 71*7. Aus 7+1+7 Elementen besteht der Rahmen einer Doppelraute (DR), zwei Doppelrauten bilden zunächst ein Achsenkreuz, das zu einem Oktaeder zusammengefügt werden kann.

2. Die beiden Verse bestehen aus 9*9 = 81 Buchstaben. 4+1 Wörter, die sich auf den Tod beziehen, sind zusammengesetzt aus 27+9 = 36 Buchstaben, ebenfalls einer Quadratzahl.

(4,547) Quin (58)

MORERE, (70)

ut (39)

merita (63)

es, (23)

FERROQUE (100)

AVERTE (67)

DOLOREM. (77)

Stirb doch, wie du es verdient hast, und beende deinen Schmerz durch das Schwert.

(10,739) Ille (36)

autem (57)

EXSPIRANS: (117)

Non (40)

me, (17)

quicumque (121)

es, (23)

inulto, (86)

Jener aber (sagte) sterbend: Wer du auch seist, du (wirst) nicht ungerächt über mich siegreich (sein).

3. Die 4+1 Wörter haben die ZW 314+117 = 431 und die Faktorenwerte (FW) 253+76 = 329. Die ZS+FS beträgt 760.

4. Denkt man sich die Zahl 2 als zwei gleiche Strecken, haben sie als Achsenkreuz im rechten Winkel und mit gleichlangen Achsenarmen die ideale Beziehung zu einander. Umgibt man sie mit einem Kreisbogen, zeigen die 4 Kreislinienpunkte 4 Phasen eines Kreislaufs mit einem Zenit und einem Tiefstpunkt. Sie können auf den Kreislauf des Lebens bezogen werden. Der Mittelpunkt und die 4 Kreislinienpunkte können von 1-5 numeriert werden. Die Addition ergibt 1-14 = 15.

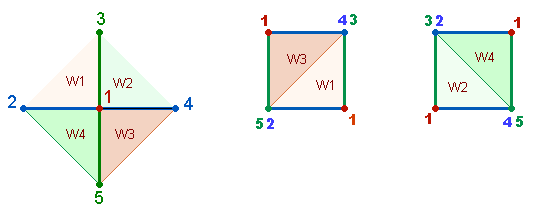
Verschiebt man einen Winkel eines Achsenkreuzes gegen den zweiten, bis die Endpunkte zusammenfallen, entsteht ein Quadrat:

nach unten

Die Grafik zeigt zwei Verschiebungsmöglichkeiten. Die Zahl 1 für den Mittelpunkt wird paritätisch an zwei Eckpunkte abgegeben. Dadurch wächst die Summe der Numerierung von 15 auf 16. Dieser Doppelaspekt von numeriertem Achsenkreuz und Quadrat ergibt die Gesamtsumme 31.

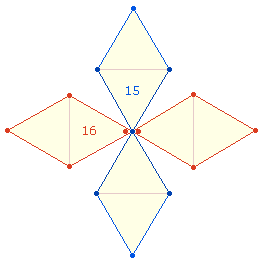
Auch der Rahmen eines DR-Kreuzes besteht aus 15+16 Elementen, wenn eine DR einen Mittelpunkt für jede Raute erhält:

5. Alle diese Aspekte versucht Vergil in den 36 Buchstaben der 5 Wörter zu vereinigen.

Das Achsenkreuz

1. Ein Achsenkreuz aus 36 Zahlen bzw. Buchstaben bedeutet, daß jedem Achsenarm ein Mittelpunkt zugewiesen wird.

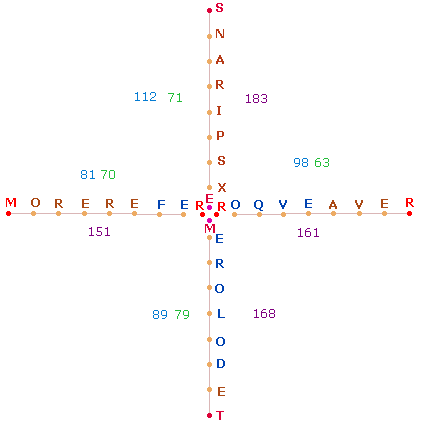
Die Aufteilung der 36 Buchstaben in zwei Hälften führt dazu, daß das Wort AVER|TE geteilt wird. Daß beide Achsen gleichberechtigt sind, zeigt sich darin, daß die ZS+FS jeder Hälfte 380 beträgt. Im Uhrzeigersinn wird der 3. Achsenarm von unten nach oben geführt und die 9 Buchstaben des 5. Wortes nach oben fortgesetzt:

2. Die ZS+FS der 4 MP-Buchstaben 51+46 = 97. Von der Gesamtsumme 760 abgezogen bleiben 663 = 3*13*17. Die ZS+FS der beiden Achsen bilden das Verhältnis (151+161):(168+183) = 312:351 = 3*13*(8:9).

3. Die ZS 34 der MP-Bu. der horizontalen Achse verhält sich zu der ZS 17 der vertikalen wie 2:1.

Die ZS der äußeren 4 Buchstaben und der 4 MP-Buchstaben beträgt 66+51 = 117, dies entspricht dem ZW des Wortes EXSPIRANS.

Die ZS der je 4 Buchstaben der horizontalen und vertikalen Achse MRRR und TMES ergeben 63+54 und bilden somit das Verhältnis 9*(7:6).

4. Die Buchstaben MR und TM des linken und unteren Achsenarms weisen in ihren ZW auf die 29 und 31 Elemente des DR-Rahmens hin.

Achsenkreuz 9+2

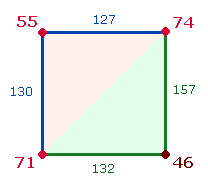
1. Ob Vergil die folgende Berechnung mit in sein Zahlenkonzept eingeplant hat, vermag ich nicht mit Sicherheit zu sagen, doch ich nehme es an: Man kann das Achsenkreuz 9 in ein Quadrat überführen und dabei die Numerierung des Achsenkreuzes 2 so hinzufügen, daß zu den ZS+FS 760 noch 16+16 hinzukommen und die Endsumme 792 = 72*11 beträgt. Nach dem Muster des oben gezeigten linken Quadrats befindet sich die 1 in der linken oberen und der rechten unteren Ecke und jeweils 7 in den beiden anderen Ecken. Es werden die ZS+FS der Eckpunkte und der Seitenteile berechnet:

Die einzelnen ZS+FS bilden verschiedene Verhältnisse: Die Eckpunkte vertikal (55+71):(74+46) = 6*(21:20), die Seitenlängen vertikal und horizontal:: (127+132): (130+157) = 7*(37:41), beide zusammen (126+259):(120+287) = 385:407 = 11*(35:37).

Die diagonalen Hälften teilen die 8 Werte in 3:5 bzw. 5:3. Die 5 Werte des linken oberen Dreiecks und 3 Werte des rechten unteren zeigen das Verhältnis 480:312 = 24*(13:20).

2. Für die Annahme der Einbindung des Musters 717 in die Quadratform sprechen – neben den bereits genannten – einige Gründe:

– Das Achsenkreuz 9 verkörpert die Grundzahlen von 1-9. Es besagt, daß 9 Begrenzungspunkte in gleichen Abständen 8 Maßeinheiten anzeigen. Die Zahlen 9 und 8 sind als Komplementärzahlen zu 1 und 2 anzusehen. Hinsichtlich der Maßeinheiten und Begrenzungspunkte ist jedoch die 1 der 8 und die 2 der 9 zuzuordnen. Die Addition der unteren und oberen Komplementärzahlen ergibt 3 und 17. Die ZS der 4 MP-Buchstaben ist 51 = 3*17. Auch die FS der 4 Eckbuchstaben ist 51. Durch Addition der Umkehrungen 81+92 erhält man 173.

Die FS der Zahlen 18 und 29 bzw 81 und 92 sind 8+29 = 37; 12+27 = 39; 37+39 = 76. Die ZS+FS ist 760. Die ZS+FS der

Die dem Wort ROTAS zuzuordnenden Zahlen der 1*1-Tabelle sind 18529. Die Summe der 3 Zahlen ist einmal mehr die Zahl 52, der ZW von OPERA und MORI.

Durch die Hinzufügung der Zahl 1 zu der MP-ZS 51 wird nicht nur das Kernmotiv 4*13 = 52 erreicht, sondern auch die ZS+FS 99, deren Faktoren 9*11 die Zahl der Maßeinheiten und Begrenzungspunkten anzeigen.

– Die Addition 36+5 ergibt die 41 Elemente eines DR-Kreuzes, das zu einem Oktaeder zusammengefügt werden kann. Aus 365 Tagen besteht das Jahr. Die FW von 36-5 unf 5-36 sind 78+144 = 222, der FW der Summe 901 ist 17*53 = 70, der ZW von MORERE. Der FW von 222 ist 42 und bildet mit 70 das Verhältnis 14*(3:5) = 112. Die Zahl 112 gibt das trinitarische Verhältnis 1:(1+2)= 1:3 wieder. Dasselbe Verhältnis zeigt sich in der Addition von 901+222 = Primzahl 1123, das analog zu 1:(1+2) als 11:(11+12) zu verstehen ist.

– Die Zahlen 9 und 8 sind auch in dem ZS+FS Gesamtergebnis 792 = 11*9*8 wiederzuerkennen.

Erstellt: Februar 2007

domum

index II