Die
Buchstaben des Carmen 85
|
ODI |
ET |
AMO |
sm |
QUARE |
ID |
FACIAM |
sm |
|
FORTASSE |
REQUIRIS |
sm |
ZS |
FS |
ZS+FS |
|
27 |
24 |
27 |
78 |
59 |
13 |
32 |
104 |
|
98 |
111 |
209 |
391 |
|
17*23 |
|
19 |
24 |
17 |
60 |
40 |
10 |
23 |
73 |
|
72 |
76 |
148 |
|
281 |
PZ |
|
46 |
48 |
44 |
138 |
99 |
23 |
55 |
177 |
|
170 |
187 |
357 |
|
|
672 |
|
NESCIO |
|
|
|
SED |
FIERI |
|
|
SENTIO |
ET |
EXCRUCIOR |
|
|
|
|
|
62 |
|
|
62 |
27 |
46 |
|
73 |
78 |
24 |
109 |
211 |
346 |
|
2*173 |
|
44 |
|
|
44 |
17 |
39 |
|
56 |
60 |
24 |
79 |
163 |
|
263 |
PZ |
|
106 |
|
|
106 |
44 |
85 |
|
129 |
138 |
48 |
188 |
374 |
|
|
609 |
|
ZS |
|
|
140 |
|
|
|
177 |
|
|
|
420 |
737 |
|
|
|
FS |
|
|
104 |
|
|
|
129 |
|
|
|
311 |
|
544 |
|
|
ZS+FS |
|
|
244 |
|
|
|
306 |
|
|
|
731 |
|
|
1281 |
|
672:609 = 21*(32:29) = 21*61; 244 = 4*61 |
||||||||||||||
I. Übersicht
1. Ich habe schon einiges über die Beziehung des carmen 85 zum SATOR-Quadrat (SQ) geschrieben. Hier soll Catulls Wahl und Zahl der Buchstaben für carmen 85 etwas systematischer untersucht werden.
Folgende Aspekte sind zu unterscheiden:
·
Unterscheidung von
Primzahl-Zahlenwerten und zusammengesetzten Zahlenwerten. Diese Unterscheidung
ist die Grundlage für die Ordnung der Zahlen nach Zahlenwerten und Faktorenwerten (FW).
·
Die Zahlensumme (ZS) und Faktorensumme (FS) der
ausgewählten Buchstaben des Alphabets
·
Die Häufigkeit dieser Buchstaben im Text
·
Die aus den 8 verschiedenen
Buchstaben des SQ ausgewählten Buchstaben
sowie ihre Häufigkeit im Text
2. Folgende Buchstaben wählte Catull für c.85 aus:
|
Bu. |
A |
C |
D |
E |
N |
R |
T |
sm |
F |
I |
M |
O |
Q |
S |
V |
X |
sm |
GS |
|
ZW |
1 |
3 |
4 |
5 |
13 |
17 |
19 |
62 |
6 |
9 |
12 |
14 |
16 |
18 |
20 |
21 |
116 |
178 |
|
FW |
1 |
3 |
4 |
5 |
13 |
17 |
19 |
62 |
5 |
6 |
7 |
9 |
8 |
8 |
9 |
10 |
62 |
124 |
|
|
7 PZ |
124 |
8 zsg. Z; Diff. 54 |
178 |
302 |
|||||||||||||
|
302 = 2*151 |
||||||||||||||||||
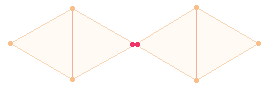
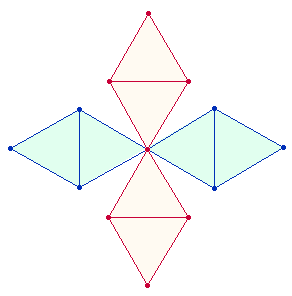
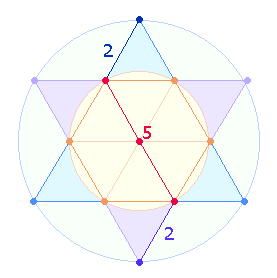
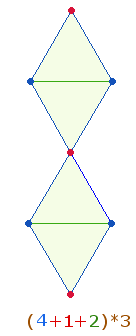
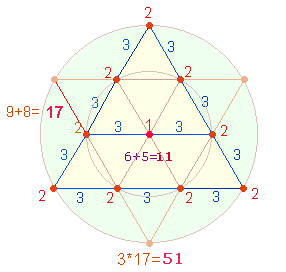
Als geometrisches Modell wählt Catull die Doppelraute (DR), deren Rahmen aus 7 Punkten und 8 Linien besteht. Die Verschränkung und Vereinigung der beiden Zickzacklinien versinnbildlicht die enge komplementäre Beziehung zwischen Mann und Frau, ebenso ergänzen sich Primzahlbuchstaben und Buchstaben zusammengesetzter Zahlenwerte. Auffallend ist zweimal die gleiche FS 62. Sie sind (vorläufig) auf je zwei Mittelpunkte einer Doppelraute und zu zweimal drei zusammengefaßte äußere Dreieckspunkte zu beziehen:
|
|
Eine DR steht nicht nur für sich allein,
sondern ist auf ein Achsenkreuz mit einer zweiten DR hingeordnet,
um zusammen einen Oktaeder
zu bilden. Darauf weisen zweimal 62
und die Summe 302 = 2*151 hin. Die
Einzelziffern der Primzahl 151 bezeichnen die Punktestruktur der DR, bestehend aus 5 hexagonalen und 2
Erweiterungspunkten. Die doppelte Summe 2*62 = 124
hat die Faktoren 4*31, deren Einzelziffern
wiederum 4+4
Punkte zweier Rauten darstellen. Denkbar sind zwei DR-Kreuze,
deren Rahmenelemente 29 bei einem und 32 bei vier Mittelpunkten betragen. Einen Hinweis
darauf gibt das ZS+FS-Verhältnis
der beiden Verszeilen 672:609 = 21*(32:29).
62 ist die ZS des Wortes NESCIO. Bemerkenswert ist die FS 44.
3. Für den Text des c.85 ergeben sich folgende Häufigkeiten:
|
a(5) e(10) i(10)
o(6) u(3) |
34 |
289 |
196 |
485 |
|
c(4) d(3) f(3) m(2) n(2) q(2) r(7) s(6) t(4) x(1) |
34 |
448 |
348 |
796 |
|
289 = 17² |
68 |
737 |
544 |
1281 |
|
Bu. |
A |
C |
D |
E |
N |
R |
T |
sm |
F |
I |
M |
O |
Q |
S |
V |
X |
sm |
GS |
|
Hfk. |
5 |
4 |
3 |
10 |
2 |
7 |
4 |
|
3 |
10 |
2 |
6 |
2 |
6 |
3 |
1 |
|
|
|
ZS |
5 |
12 |
12 |
50 |
26 |
119 |
76 |
300 |
18 |
90 |
24 |
84 |
32 |
108 |
60 |
21 |
437 |
737 |
|
FS |
5 |
12 |
12 |
50 |
26 |
119 |
76 |
300 |
15 |
60 |
14 |
54 |
16 |
48 |
27 |
10 |
244 |
544 |
|
|
35 PZ |
600 |
33 zsg.Z;
Diff. 193 |
681 |
1281 |
|||||||||||||
Die
ZS 300 ist die Summe der Zahlen von 1-24. Die Buchstaben CD mit der ZS 24 gehören nicht zu den SQ Buchstaben. 276 ist daher die Summe der Zahlen von 1-23. 23 und 24 sind Konstitutivzahlen für ihre Summe 47,
die ZS für DEUS
– Gott. Die ZW+FW der beiden Zahlen sind 23+23 = 46 und 24+9 = 33. 46+33 = 79 ist die ZS+FS von LESBIA.
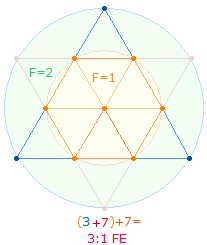
Der FW von 300 ist 3+7+7 = 17. (3+7):7 Punkte des Tetraktyssterns und Hexagons bedeuten 3:1 Kreisflächeneinheiten der beiden konzentrischen Kreise:
|
|
Das Hexagon und seine Erweiterung zum Tetraktysstern enthalten jeweils 12 Linien, zusammen 24.
4. Von den 8 Buchstaben des SATOR-Quadrats fehlt in Carmen 85 das P. Die ZS und FS der 7 SQ Buchstaben – einfach und nach Häufigkeit – sind folgende:
|
Bu. |
A |
E |
N |
R |
T |
sm |
O |
S |
sm |
GS |
|
|
|
|
|
|
|
|
|
|
|
|
|
ZW |
1 |
5 |
13 |
17 |
19 |
55 |
14 |
18 |
32 |
87 |
|
FW |
1 |
5 |
13 |
17 |
19 |
55 |
9 |
8 |
17 |
72 |
|
|
|
|
|
|
|
110 |
|
|
49 |
159 |
|
Bu. |
A |
E |
N |
R |
T |
sm |
O |
S |
sm |
GS |
|
Hfk. |
5 |
10 |
2 |
7 |
4 |
23 |
6 |
6 |
12 |
35 |
|
ZS |
5 |
50 |
26 |
119 |
76 |
276 |
84 |
108 |
192 |
468 |
|
FS |
5 |
50 |
26 |
119 |
76 |
276 |
54 |
48 |
102 |
378 |
|
|
|
|
|
|
|
552 |
|
|
294 |
846 |
|
846 = 18*47; 552 = 24*23 |
||||||||||
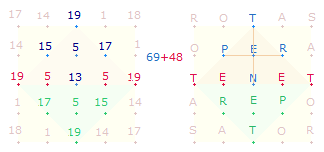
Die ZS 276 = 4*69 hat zwei Bedeutungen im SQ: erstens, die ZS des SQ-Rahmens, je zweimal SATOR ROTAS – Schöpfer, du drehst, zweitens, vier innere Rautenquadrate, deren ZS aus 2*32+5 bestehen:
|
|
Die 5 Buchstaben ergeben einen Sinn, wenn man sie bei Verdoppelung des E mit SATOR verbindet: SATOR PERNET – der Schöpfer webt unaufhörlich. Übrig bleiben zweimal die Buchstaben ET – vom Mittelpunkt aus gelesen.
552 ist die ZS+FS des SATOR-Quadrats: 303+249.
5. Die Vermutung, Catull habe das SQ in seine gematrische Konstruktion integriert, bestätigt sich auf folgende Weise:
|
|
SQ |
c. 85 |
sm |
|
ZS |
303 |
737 |
1040 |
|
FS |
249 |
544 |
793 |
|
|
552 |
1281 |
1833 |
|
793:1040 = 13*(61:80) = 13*141 |
|||
|
141 = 3*47 |
|||
FS und ZS sind durch 13 teilbar. Vorbild ist die ZS 182 = 14*13 von SATOR OPERA TENET – Der Schöpfer erhält seine Werke. Nun entsprechen 846 = 18*47, der ZS+FS der 8 Buchstaben im SQ. Die Differenz 435 zur Gesamt ZS+FS 1281 + die ZS+FS 552 = 23*24 beträgt 987 = 21*47. Die Zahlen 18 und 21 haben eine doppelte Bedeutung: Erstens, der Tetraktysrahmen besteht aus 9 Punkten + 9 Linien. Zählt man jede Tetraktysseite gesondert, werden die Eckpunkte doppelt gezählt und das Ergebnis ist 18+3 = 21. Zweitens, die DR besteht aus 7 Punkten, 10 Linien und 4 Dreiecksflächen, zusammen aus 21 Elementen. Die entsprechenden FW sind 7+7+4 = 18.
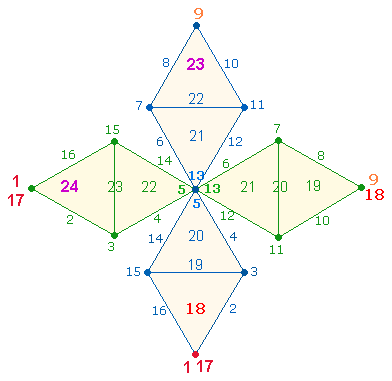
Die Zahl 987, die Komplementärzahl zu 123, ist die Summe der ZS+FS der Zahlen 23 und 24: 276+300 = 576; 201+210 = 411; 576+411 = 987. Der Umkehrung von 01 und 10 entsprechend lassen sich die Zahlen 1-23 und 1-24 verschieden auf die Elemente der DR eintragen:
|
|
Die Zahl 1833, aufgeteilt in 18+33 = 51 bezeichnet zweimal die ZS der 4+4 verschiedenen Buchstaben des SQ in zwei Hälften des Wortes PENSATOR – der im Gleichgewicht Haltende, der Vergeltende:
|
P |
E |
N |
S |
A |
T |
O |
R |
|
15 |
5 |
13 |
18 |
1 |
19 |
14 |
17 |
1. Das schwierig zu lösende Rätsel ist die ZS+FS 294, die durch die Buchstaben OS zustande kommen. Die beiden Buchstaben kommen in jeder Verszeile je dreimal vor. Das Außerodentliche der Zahl 294 ist, daß sie aufgeteilt in 106+188 die ZS+FS von NESCIO EXCRUCIOR und IESUS CHRISTUS ist.
|
|
ZS |
FS |
sm |
|
ZS |
FS |
sm |
|
NESCIO |
62 |
44 |
106 |
IESUS |
70 |
36 |
106 |
|
EXCRUCIOR |
109 |
79 |
188 |
CHRISTUS |
112 |
76 |
188 |
|
|
171 |
123 |
294 |
|
182 |
112 |
294 |
Wenn man annimmt, daß die Zahlenwerte für IESUS CHRISTUS eine vollkommene Begründung im Bedeutungssystem der Zahlen haben, muß Catull objektive Kenntnis davon gehabt haben. Das heißt aber, das Erkennen von Zahlenbedeutungen ist möglich, wenn man bestimmte rationale Regeln und Mittel beachtet und anwendet.
Die Zusammenhänge sind sehr komplex und manches kann nur vermutet werden. Ich versuche, der Reihe nach die Zusammenhänge darzulegen:
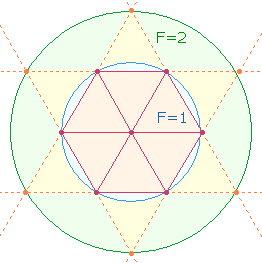
2. Unverzichtbarer Ausgangspunkt ist der Tetraktysstern und dessen zwei konzentrischen Kreise:
|
|
|
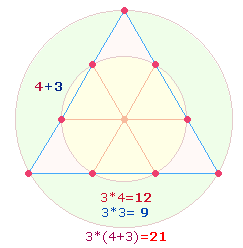
Zwei Kreisflächenverhältnisse sind möglich: Das Flächenverhältnis des hexagonalen Kreises zum erweiterten Tetraktyskreis ist 1:3 und zum äußeren Kreisring 1:2. Daraus ergeben sich 4+3 = 7 Kreisflächeneinheiten, auf die alles ausgerichtet ist.
Unverzichtbares Gesetz ist auch die Unterscheidung zwischen Maß und Zahl. Ein Längenmaß ist nur faßbar, wenn es durch zwei Punkte begrenzt wird. Aus diesem Grund bedarf das Dezimalsystem 11 Begrenzungen für 10 Maßeinheiten:
|
|
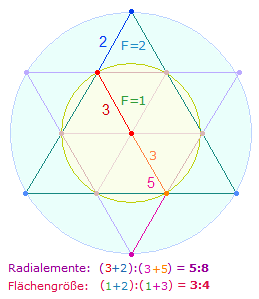
Mittelpunkt, Punkte, Linien und Flächen sind zweidimensionale geometrische ELEMENTE, die von 1-4 numeriert werden können. Diese numerischen Elemente bilden mit den Kreisflächeneinheiten eine ANALOGISCH gültige vielfältige VERKNÜPFUNGEN. Daher gehören z.B. 5:8 Radialemente und 3:4 Flächeneinheiten zusammen. Die Kreisflächenverhältnisse können auch zu 2:1 und 3:1 umgekehrt werden.
Durch hexagonale Erweiterung wird ein (sanduhrförmiges) Doppeldreieck zu einer Doppelraute (DR). Drei Doppelrauten und zwei Tetraktys bilden zwei komplementäre Modelle, die für das Dezimalsystem relevant sind. Eine Tetraktys besteht aus 37, eine DR aus 21 Elementen, die Tetraktys aus 10 Punkten, die DR aus 10 Maßeinheiten. Die Addition 37+21 = 58 weist auf 5:8 Radialelemente hin. Zwischen zwei Einzelziffern und ihrer zweistelligen Zusammensetzung besteht eine innere Verwandtschaft.
3. Ein Kreisdurchmesser besteht sowohl aus 5 Durchmesserelementen als auch aus 2*3 Radialelementen, der Tetraktyskreis – einschließlich des hexagonalen Kreises – aus 9 Durchmesserelemenen und 2*5 Radialelmenten. Für die Radialelemente ergeben sich dadurch die Zahlen 6 und 10 bzw. 10 und 6, zusammen 16. Diese Zahl ist wegen zweier Radien eines Kreises auf 32 zu verdoppeln.
Eine Zahl kann von 1 ab bis zu ihr selbst addiert werden. Die Numerierungssummen von 3 und 4 Kreisflächeneinheiten sind demnach 6+10 = 16, ebensoviel wie für die Addition der doppelten Radialelemente ermittelt wurde. Die Zahl 16 spielt also eine wichtige Rolle im Bedeutungsschema der Zahlen. Als Einzelziffern bezeichnen sie Mittelpunkt + 6 Kreislinienpunkte.
4. Die Doppelraute steht nicht nur für sich allein, sondern bildet mit einer zweiten ein Achsenkreuz, das durch Faltung der Mittellinien und Vereinigung der äußeren Punkte zu einem Oktaeder zusammengesetzt werden kann. So kommt der Tetraktysstern zu seinem dreidimensionalen Ziel:
|
|
|
|
Der Oktaeder zeigt zwei entgegengesetzte Pyramiden, also eine vollkommene Form dreidimensionaler Umkehrung.
5. Es fällt auf, daß die Buchstaben der 14.-18. Position des lateinischen Alphabets aus Rundungen und Flächen bestehen: O P Q R S. Sie können mit der DR und der Okaederbildung in Verbindung gebracht werden. Besteht eine DR aus den Rahmenelementen von 7 Punkten + 8 Linien, so werden die durch die Vereinigung der beiden äußeren Punkte die Zahl der Punkte von 7 zu 6 verkürzt, und man erhält die Konstitutivzahlen 6+8 bzw. 8+6 und den 14. Buchstaben O. Der Buchstabe S mit dem Zahlenwert (ZW) 18 = 2*9 ist von den zwei DR-Zickzacklinien her zu verstehen, die den Rahmen der DR bilden.
Die Einzelziffern der Zahlen 14 und 18 bezeichnen den Mittelpunkt + 4 und 8 Durchmesserelemente der DR-Zickzacklinie in der Bedeutung des Kreisflächenverhältnisses 1:3. Die Multiplikation 14*18 hat dasselbe Ergebnis wie die der Umkehrzahlen 12*21 – die Palindrom- und Umkehrzahl 252:
|
|
|
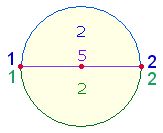
Das Prinzip der Umkehrung wird bei Teilung eines Kreises erkennbar, wenn die zwei Schnittpunkte mit 1 und 2 bezeichnet werden.
6. Das Bedeutungssystem der Zahlen ist erst dann erforschbar und durchschaubar, wenn sie mit ihren Faktorenwerten (FW) in Verbindung gebracht werden. Für die Zahlen 14-18 ergibt sich folgendes FS:ZS-Verhältnis:
|
ZW |
14 |
15 |
16 |
17 |
18 |
80 |
|
FW |
9 |
8 |
8 |
17 |
8 |
50 |
|
|
23 |
23 |
24 |
34 |
26 |
130 |
|
50:80 = 10*(5:8) |
||||||
Das FS:ZS-Verhältnis 5:8 bedeutet gleichzeitig, daß die Differenz zwischen FW und ZW 3 beträgt. Man kann es als internes Verhältnis 5:3 bezeichnen. 5:8 Radialelementen entsprechen, wie oben dargelegt, die Kreisflächenverhältnisse 1:2 und 1:3. In zweistelliger Zusammensetzung ergibt sich bei doppeltem Radius 2*(12+13) = 50. 50+80 läßt sich auch aus der Addition von ZW und FW zusammensetzen.
Die FS 50 hat besondere Relevanz zu den Umkehrzahlen 12+21 = 33, da deren FW 7+10 = 17 sind und somit die ZS+FS 50 beträgt. 7 hexagonale Punkte zu 10 Tetraktyspunkten aber bedeutet das Kreisflächenverhältnis 1:3.
7. Es scheint, daß die ZS+FS 80+50 der Zahlen 14-18 für so bedeutsam gehalten wurden, daß sie zur Grundlage des römischen Zahlensystems gemacht wurde, das sich 7 Buchstaben bediente:
|
ZZ |
C |
D |
I |
L |
M |
V |
X |
|
|
|
Zahl |
100 |
500 |
1 |
50 |
1000 |
5 |
10 |
1666 |
|
|
ZW |
3 |
4 |
9 |
11 |
12 |
20 |
21 |
80 |
|
|
FW |
3 |
4 |
6 |
11 |
7 |
9 |
10 |
50 |
|
|
1666 = 2*7²*17 |
|||||||||
8. Sowohl die Tetraktys als auch die DR bietet die Möglichkeit, die Umkehrzahlen 12 und 21 darzustellen. Es geht hierbei jeweils um die Erweiterung des Teils zum Ganzen:
|
|
|
Eine Tetraktysseite besteht aus 4 Punkten und 3 Linien. Auf diese Weise erhält man durch 3*4 = 12 und 12+3*3 die Gesamtzahl 21. In der Tetraktys sind die Produktzahlen umgekehrt 4*3 "Dachelemente" und 3*3 Längsachsenelemente ergeben ebenfalls 12 und 12+9 = 21. Catull hat dies in carmen 85 verwirklicht durch 3 D = 12 und 4 C = 12.
9. Die Doppelraute besteht aus 5 hexagonalen und 2 Erweiterungspunkten. Daraus ergibt sich das Punktemuster 1-5-1. 151 in dreistelliger Zusammensetzung ist eine Primzahl. Bei der Festlegung der 7 Zahlenbuchstaben hätte man von hier aus bereits weiter gehen können. Offensichtlich aber stellte man noch eine weitere Berechnung an. Wenn man die 4 Punkte und 3 Linien einer Tetraktysseite mit 2 und 3 numerierte, erhielt man für drei Seiten 51 – ohne Mittelpunkt. Diesen konnte man nun vor 51 und nach 51 setzen und erhielt so 151 und 511. Auch konnte man das Punktemuster der DR als 15 Rahmenelemente + zweiten Mittelpunkt lesen:
|
|
Der FW von 511 = 7*73 = 80. Die Einzelziffern der beiden Faktoren sind auf die 7 Punkte des Hexagons und die 10 Punkte der Tetraktys zu beziehen und stellen somit das bekannte Kreisflächenverhältnis 1:3 dar.
Die Summe der Zahlen 1-21 beträgt 21*11 = 231. Der FW 151 der Primzahl 151 und der FW 80 der Zahl 511 ergeben nun eben die Summe 231. Nun kommt noch die Zahl 115 = 5*23 = FW 28 hinzu. Die Einzelziffern 5 und 2+3 geben die 10 Radialelemente der DR-Zickzacklinie wieder. Wenn man die ZS 115 mit der FS 50 der 7 Zahlbuchstaben verbindet, erhält man die FS 165 der Zahlen 1-21.
Die Addition der drei FW 151+80+28 ergibt 259 = 7*37. Das FS:ZS-Verhältnis der drei Umkehrzahlen beträgt demnach 259:777 = 37*(7:21) = 37*28. Hier liegt eine Begründung für die 7 römischen Zahlzeichen.
10. Nun besteht die DR aus 4 Dreiecken, 7 Punkten, 2 Querlinien und 8 Rahmenlinien, sodaß die Multiplikation 4*7 der ersten beiden Zahlen die zusammengesetze Zahl 28 ergibt. Sie gibt einen bedeutenden Hinweis auf ein Sinnprinzip des Zahlensystems, das schon bei der Doppelung von 5 Durchmesserelementen und 6 Radialelementen des Hexagons in Erscheinung trat, nämlich, daß Doppelzählungen sinnvolle Ganzheiten bilden.
Die Doppelzählung in der DR ergibt sich nun daraus, daß ein einzelnes Dreieck aus 7 Elementen besteht, sodaß für 4 Dreiecke 28 Elemente gezählt werden müßten. Die 21 = 3*7 Elemente der DR enthalten also ein Dreieck mehr. Theologisch wird dadurch die Vorstellung geweckt, daß drei göttliche Personen eine einzige vollkommene Gemeinschaft bilden. Es ist dabei zu bedenken, daß die DR um 4 Elemente über die Fischfigur der Tetraktys hinauswächst, die mit ihren 17 Elementen drei Dreiecke umfaßt. Die Fischfigur also ist bereits die Bezugsfigur für drei göttliche Personen:
|
|
Hier ist anzumerken, daß die ZS+FS von CATULLUS 103+71 = 174 beträgt, Catull den Aspekt von 17+4 Elementen besonders berücksichtigt.
Entsprechend den 3+4 Kreisflächeneinheiten ist also eine Doppelzählung von 3*7 + 4*7 = 7*7 = 49 Dreieckselementen vorzunehmen. Da nun der Tetraktysstern drei DR enthält und diese zweimal für drei Oktaeder verwendet werden, ist 49 mit 6 zu multiplizieren. Deshalb hat Catull auch darauf geachtet, daß jede Verszeile dreimal OS enthält.
11. Es ist nun die Frage zu beantworten, wie es zu der Aufteilung der Zahl 294 in 106+294 kommt. Folgender innerer Zusammenhang könnte bestehen: Ausgangszahlen sind die beiden FW 80 und 151 der Zahlen 511 und 151. 80 ist durch zweimal 5*8 = 40 als Radialelemente interpretierbar, ergibt als Addition 26 und ist zu 80 hinzuzufügen. Die Summe 106 zeigt wiederum durch 2*53 in den Einzelziffern die Radialelemente 5:3 in der Bedeutung des Kreisflächenverhältnisses 3:1. Die Umkehrung 2*35 erscheint in der ZS 70 von IESUS.
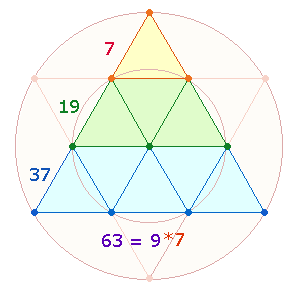
Von 151 zu 188 ist 37 hinzuzufügen. Der Faktor 37, der ja entscheidend in den Umkehrzahlen von 151 hervorgetreten ist, ist die Zahl der Tetraktyselemente. Nun enthält die Tetraktys 9 Dreiecke, die mit 7 multipliziert 26+37 = 63 ergeben:
|
|
Die Zahlendreieck der Tetraktys besteht aus drei Dreiecksstufen, die aufaddiert 63 Elemente ergeben. Die beiden ZS+FS 106 und 188 verbinden also die DR, deren 21 Elemente, von 1-21 gezählt, 231 = 33*7 betragen, mit 9*7 Dreieckselementen der Tetraktys. Das Verhältnis 33:9 = 3*(11:3) = 3*14 ergänzt die 11 Elemente der Raute durch drei weitere Elemente zu 2*7 Dreieckselementen.
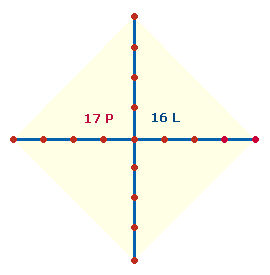
Die Zahl 188 kann sich auf die 17 Elemente der Fischfigur beziehen: Mittelpunkt + 5 Punkte + 3 Flächen und 8 Linien oder auf ein Achsenkreuz AK5 aus 17 Punkten, die gemäß der Zahl 106 = 10+6 16 Linien begrenzen:
|
|
17+16 = 33 bildet die Mitte der Umkehrzahlen 12+21.
Die ZW/FW-Verrechnung der Zahlen 106 und 188 führt zweimal zu 106 zurück:
|
|
|
|
sm |
FW |
sm |
FW |
sm |
FW |
sm |
|
|
106 |
188 |
294 |
19 |
|
|
|
|
|
|
FW |
55 |
51 |
106 |
55 |
|
|
|
|
|
|
sm |
|
|
400 |
74 |
474 |
84 |
|
|
|
|
FW |
|
|
18 |
39 |
57 |
22 |
|
|
|
|
sm |
|
|
|
|
531 |
106
|
637 |
27 |
|
|
FW |
|
|
|
|
65 |
55 |
120 |
14 |
|
|
798 = 42*19 = FW
12+19 = 31 |
757 |
41 |
798 |
||||||
Mit den Primzahlen 757 und 41 kommt die Verrechnung an ihr natürliches Ende. Aus 42*7 = 294 wird 42*19 = 798.
12. Wegen ihres theologischen Gehalts kommt auch die Fischfigur für eine Doppelzählung in Frage: Nach gleichem Muster wie bei den 21 Elementen der DR ist 17+21 = 38 mit 2*3 zu multiplizieren: 6*38 = 228. Nun kann man beide Doppelzählungen addieren: 49+38 = 87. Die doppelte Summe 174 ist wiederum die ZS+FS von CATULLUS. Die Zählung beider Paarungen 294+228 ergibt die ZS+FS 522 = 18*29, deren Einzelziffern die 9 Durchmesserelemente der beiden konzentrischen Tetraktyskreise wiedergeben. Tatsächlich hat Catull diese Zahl in seiner Versstruktur untergebracht. Diese hat zwar verschiedene Facetten, aber eine Kompositionsvariante richtet sich nach den 5 Durchmesserelementen der Kreisachse. Die ZS+FS findet sich in den Wörtern, die den beiden Radialmaßen entsprechen:
|
ET |
AMO |
QUARE |
ID |
FACIAM |
FORTASSE |
REQUIRIS |
||
|
27 |
24 |
27 |
59 |
13 |
32 |
98 |
111 |
|
|
19 |
24 |
17 |
40 |
10 |
23 |
72 |
76 |
|
|
46 |
48 |
44 |
99 |
23 |
55 |
170 |
187 |
|
|
NESCIO |
SED |
FIERI |
SENTIO |
ET |
EXCRUCIOR |
|||
|
62 |
27 |
46 |
78 |
24 |
109 |
|||
|
44 |
17 |
39 |
60 |
24 |
79 |
|||
|
106 |
44 |
85 |
138 |
48 |
188 |
|||
|
|
99+67 = 166 |
|
200+156 = 356 |
|
||||
|
166+356 = 522 |
||||||||
Die gelb unterlegten Werte ergeben 294, die übrigen 228.
Die ZS+FS der 3 Punktepositionen beträgt 759 = 3*23*11 = FW 37. 465 ist die ZS, 294 (106+188) die FS der Zahlen 1-30. Die violett unterlegten Werte betragen 186, wodurch sich mit der übrigen Summe 279 das Verhältnis 93*(2:3) ergibt. Die FW von 522 (2 Linien) und 759 (3 Punkte) sind jeweils 37.
Erstellt: November 2022