SPQR (II): Römische Identität im Buchstaben- und Zahlenmodell SPQR

SPQR

Teil 2

VI. SPQR und das Achsenkreuz 5

a) Diagonalhälften des Quadrats

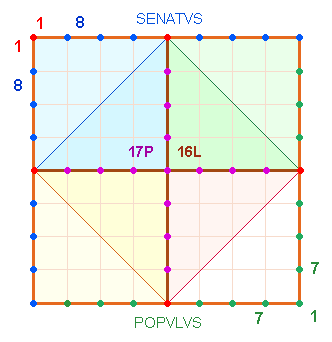
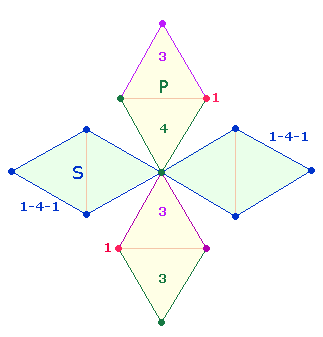
1. Das Achsenkreuz 5 (AK5) hat die Grundzahlen von 1-9 als Radialelemente (5P+4L). Die 17 Punkte und 16 Linien (=Maßeinheiten) des AK5, Herzmitte der die Kreisumdrehung kennzeichnenden Zahlen 12 bis 21, bilden das Grundgerüst römischer Identität. Durch Ausfaltung seiner 4 Winkel werden die Umrisse eines Quadrats von der Größe 8*8 abgesteckt. Diese Umgrenzungslinie des AK5 stellt gewissermaßen das POMERIUM des römischen Bewußtseins dar:

Das S und das P umfahren die Umrißlinie, indem sie nur die Punkte besetzen: Senat und Volk teilen sich zwei diagonale Flächenhälften. Eine Diagonalhälfte eines Quadrats beginnt und endet in einem Winkelpunkt, die andere Hälfte beginnt und endet mit einer Maßeinheit.

Eine Seitenlänge besteht aus 9 Punkten. Das S mit dem Zahlenwert (ZW) 18 beansprucht also 2*9 Punkte. Das bedeutet, daß der Winkelpunkt der beiden Seiten doppelt besetzt ist.

Das P besetzt die 15 Punkte der zweiten Rahmenhälfte.

2. Die Anpassung der beiden Buchstaben an den Quadratrahmen könnte man als willkürlich betrachten, wenn die doppelte Zählung von 2*9 und 7-1-7 nicht auch auf den Rahmen der Doppelraute (DR) anwendbar wäre:

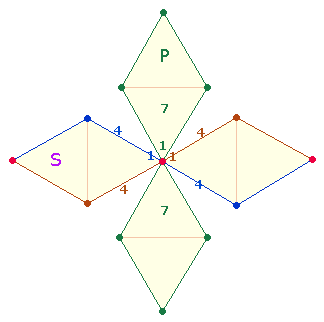
Der Rahmen einer DR besteht aus zwei sich kreuzenden Durchmesserlinien von je 5P+4L. Dabei werden die 3 Vertikalpunkte doppelt besetzt. Nach Abzug der 3 überzähligen Besetzungen bleiben 7P+8L für das P übrig:

Die Aufteilung nach Punkten und Linien beider Zählungen ergibt 10+7 = 17 Punkte und 8+8 = 16 Linien, dieselben Werte wie im AK5.

3. Ein DR-Kreuz besteht aus 21+20 = 41 Elementen, wenn man den Mittelpunkt (MP) einfach zählt. Diese Zahl stimmt mit der FS von SPQR überein.

Zwei Doppelrauten kann man zur geschlossenen Form eines Oktaeders zusammenfügen. Das bedeutet eine kreisförmige Bewegung zur Mitte und Umkehr zum Anfang. Eine Umkehrform zeigen auch die Faktorensummen der Zahlen 1-21 und 1-41: 156 und 516.

Die Zahl der Linien und Punkte des Achsenkreuzes 5 selbst und des Quadratrahmens ist 16 und 50 und enthält eben diese Umkehrzahlen. Dieselben Zahlen erhält man, wenn man von 66 Gesamtelementen 5 Doppelbesetzungen (rote Punkte in der Grafik) abzieht und die Zahl 61 übrig bleibt.

b) Rechteckhälften des Quadrats

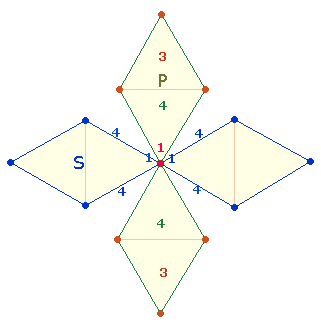
1. Die beiden Grafiken zeigen in der Zahlenfolge 7-1-7 Übereinstimmung in der Anordnung der 15 P-Elemente des DR-Rahmens, aber unterschiedliche Abfolgen für die 2*9 DM-Elemente des S.

Auch inhaltlich kann die diagonale Einteilung der Quadrathälften nicht ganz befriedigen. Denn die 15 Punkte des P = POPVLVS, dem das Verbindungswort QVE angehängt wird, sollte im Quadratrahmen so verlaufen, daß der 15. Punkt unmittelbar vor dem Achsenkreuz zu stehen kommt. Genau dies ist der Fall, wenn die erste Quadrathälfte im Mittelpunkt einer Seitenlänge beginnt. Nun herrscht Übereinstimmung in der Zahlenfolge 4-1-4 zwischen Doppelraute und Quadrat. Der MP der 2. Seitenlänge ist jetzt dreimal besetzt.

Die 15 Punkte des P hingegen verlieren ihr früheres Einteilungsmuster im DR-Rahmen, sie verlaufen nun nach Punkten und Linien geschieden: 3-1-3 + 4-4. Je 4 Linien gehören zu einer Raute. Mittelpunkt und Winkelpunkt der Quadratseite bezeichnen jeweils den Anfang von 4 Linien:

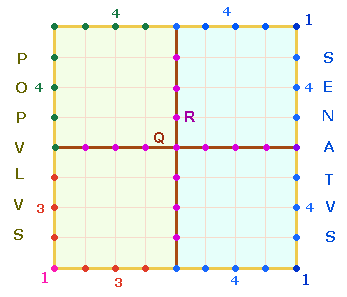
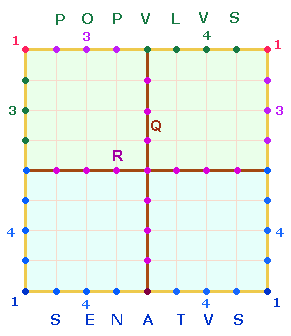
Das Quadrat 5 ist nun in zwei Rechtecke und jedes Rechteck in zwei weitere Quadrate unterteilt.

Nach vorliegender Grafik besetzt SENATVS die rechte und POPVLVS die linke Quadrathälfte, wenn man vorher festlegt, daß die beiden rechtwinkligen Achsen in einer Bewegung von links nach rechts und von unten nach oben durchlaufen werden und der letzte Punkt der Vertikalachse gleichzeitig der erste von 18 Punkten des S ist. Tatsächlich ist der letzte Buchstabe von ROMANVS auch der erste Buchstabe von SENATVS. (Um von der horizontalen zur vertikalen Achse zu gelangen, werden – im rechten unteren Winkel – in Schleifenform 3+1+3 = 7 Elemente erfaßt, die man den 33 Elementen der beiden Achsen hinzurechnen kann, über deren Relevanz hier jedoch nicht weiter nachgedacht werden soll.)

Auch die Punkte des Quadratrahmens werden – im Uhrzeigersinn – nacheinander durchlaufen und enden vor dem obersten Punkt der Vertikalachse. Von dort wiederholt sich das Abschreiten von Punkten und Linien der Achsen Q und R. Nun liegt der Anfangspunkt von SENATVS, um 90° gedreht, im Mittelpunkt der rechten Seitenlänge und derjenige von POPVLVS im MP der rechten Quadratseite. Wenn man sich den Bewegungsablauf fortgesetzt denkt, wechseln SENATVS und POPVLVS ständig ihre Positionen. In die geordneten Kreisläufe des Kosmos wird so auch das Leben der menschlichen Gemeinschaft eingebunden.

2. Das vorliegende Modell zweier Quadrathälften für SPQR sollte eigentlich genügen. Aber wie weiter unten ersichtlich sein wird, gesellt sich ein weiteres Modell sinnvoll hinzu, obwohl seine inhärente Logik nicht zwingend erscheint. Punkte und Linien wurden im ersten Modell (7-1-7) in einer einzigen Abfolge zusammengefaßt. Das zweite Modell trennt Punkte und Linien in zwei Abläufen (3-1-3, 4-4). Im dritten Modell wechseln Punkte und Linien in zwei Abfolgen (3-1-3, 4-1-3) ab: Die erste Folge beginnt mit dem untersten Punkt und nimmt die rechte und linke Linie hinzu (P-L-L). Dem darüber liegenden Punkt entspricht der Mittelpunkt der linken Quadratseite (P). Es folgt nun der rechte Punkt, die nächste rechte und linke Linie (P-L-L). Der Mittelpunkt der Doppelraute findet seine Entsprechung im Mittelpunkt der linken Quadratseite und markiert den Beginn einer Folge von 4 Elementen (P-L-L-P). Der rechte obere Punkt liegt nun im oberen linken Winkel (P) des Quadratrahmens. Es folgen die restlichen 3 Elemente (L-L-P):

c) Auswertung der 3 Modelle

1. Man kann die ermittelten Abfolgen von Einzelzahlen als drei- bzw. zweistellige Zahlen zusammenfassen und prüfen, ob sie sinnvolle Ergebnisse liefern.

2. Tatsächjlich lassen die Zahlen des 3. Modells eine bemerkenswerte Verbindung zum SATOR-Quadrat erkennen. Dort umlaufen das Wort SATOR und seine Umkehrung ROTAS den Quadratrahmen. Die ZW der Vokale A und O ergeben 15 und die ZW der Konsonanten STR 54, zusammen 69. Beide ZW sind durch die Formel 6+9 und 6*9 miteinander verbunden.

Die Zahlenwert/Faktorenwert-Verrechnung führt zu folgendem Ergebnis:

	ZW	FW	Sm.
S	414	31
	414	31
P	313	313
	413	66
Sm.	1554	441
Fakt.	6737	21*21
FW	49	20	69
Verh.	21*(74:21)

Die Zahlensumme 1554 spiegelt die ZW der Vokale und Konsonanten des Wortes SATOR wider, die FW 49+20 führen wiederum zum Gesamt-ZW 69.

3. Wenn man die Zahlenwerte aller 3 Modelle berücksichtigt, ergibt sich zwischen SENATVS und POPVLVS folgendes Verhältnis:

	S		P		Sm.	FW	FW
Mod.1	81	18	717		816	28
Mod.2	414	414	313	44	1185	87
Mod.3	414	414	313	413	1554	49
	1755		1800			164	45
Verh.	45*(39:40)				3555		90
					45:90 = 45*(1:2)

Die beiden Verhältniszahlen 39 und 40 sind angrenzend und daher konstitutiv für die Summe 79. Die zweimal auftretende gemeinsame Teilungszahl 45 verweist auf die 9 Durchmesserelemente, da 45 die Summe der Zahlen von 1 bis 9 ist.

Das Teilungsverhältnis 1:2 der Faktorenverrechnung zeigt die beiden Zahlen, die die Grundlage jeder zyklischen Umkehrbewegeung bilden. Die drei Modelle bilden selbst ein 1:2-Verhältnis, da die Zahl 79 in 1185 15-mal, und in 816+1554 = 2370 30-mal enthalten ist.

Erstellt: August 2005

Erweitert: September 2005

index