Die
Kreuzesinschrift als magisches Quadrat
C. Die Zahlenwerte der 18 symmetrischen
Quadrate
|
|
|
1. Die
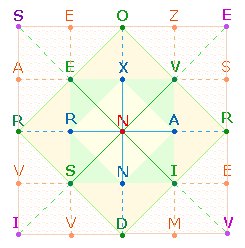
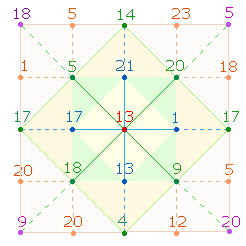
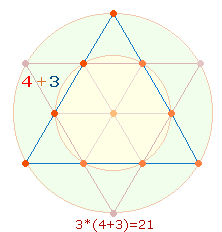
Erkenntnis, daß es im 5x5 Punkte-Quadrat (Qu5) 6 symmetrische Punktegruppen gibt und
darin 18 Quadrate, 9 Rautenquadrate und 9 Vollquadrate (Qu3) Platz finden, bietet die Möglichkeit, nach weiteren Ordnungen durch
Ermittlung der Zahlenwerte (ZW) zu suchen.
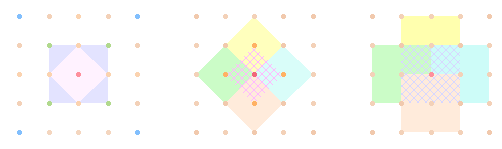
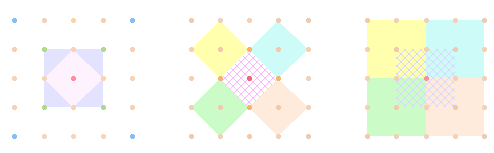
Die beiden
Quadratformen sind entweder an den beiden Mittelachsen oder den Diagonalachsen
ausgerichtet:
|
|
|
|
Ein
Rautenquadrat besteht aus 5, ein Vollquadrat aus 9 Punkten, zusammen 14 Punkten. Die 18/2 Quadrate besetzen daher 9*14 = 126 Punkte.
2.
Die Zahlensummen (ZS) der 16 einzelnen Quadrate sind unterschiedlich, aber wie bei
jedem der 2 Mittelquadrate sind die Werte von je
4 Quadraten einer Symmetriegruppe zusammen durch 13 teilbar. Eine weitergehende innere Ordnung ist daher nur an den Faktorenwerte (FW) der einzelnen ZS erkennbar. Entsprechend dem Verlauf
des Quadrats von der linken unteren Ecke nach oben, von dort nach unten und
wieder von unten nach oben sollen die ZS und ihre FW in drei Bahnen, links, Mitte und rechts, tabellarisch erfaßt werden:
|
Rautenquadrate |
Vollquadrate |
||||||||||||||
|
links |
Mitte |
rechts |
Sm. |
Sm. |
links |
Mitte |
rechts |
Sm. |
Sm. |
||||||
|
ZS |
FW |
ZS |
FW |
ZS |
FW |
|
|
ZS |
FW |
ZS |
FW |
ZS |
FW |
|
|
|
49 |
14 |
73 |
73 |
83 |
83 |
205 |
170 |
111 |
40 |
119 |
24 |
132 |
18 |
362 |
82 |
|
70 |
14 |
65 |
18 |
60 |
12 |
195 |
44 |
125 |
15 |
117 |
19 |
117 |
19 |
359 |
53 |
|
88 |
17 |
57 |
22 |
40 |
11 |
185 |
50 |
131 |
131 |
107 |
107 |
94 |
49 |
332 |
287 |
|
207 |
45 |
195 |
113 |
183 |
106 |
585 |
264 |
367 |
186 |
343 |
150 |
343 |
86 |
1053 |
422 |
Auffällig sind die identischen ZS 195 für die Rautenquadrate der Mittelachsen.
3.
Die Summe der FW ist 264+422 = 686 = 2*7*7*7. Diese Faktorensumme (FS) gibt die 3*7 Elemente von 2 Tetraktysrahmen wieder:
|
|
In der Produktaufteilung 14*49 erscheinen die Einzelziffern der 9*14 Punktepositionen der
beiden Quadratformen wieder.
Die Zahl 686 wiederholt sich durch
die zweimalige ZS 343 für die mittlere und rechte Bahn der VQ.
Auf die
Tetraktys, die aus 10 Punkten + 9 Dreiecken + 18 Linien = 37 Elementen besteht, weisen die FW 19+18 der beiden
Mittelquadrate hin.
Nach Abzug
der Zahl 37 bleibt die FS 649 = 11*59 übrig. Die Einzelziffern der Zahl 59 entsprechen
den 5 und 9 Punkten der beiden
Quadratformen.
4.
Ohne die FS der 2 Mittelquadrate lassen sich 4 Gruppen von
jeweils 4 FW bilden:
|
|
RtQ |
VQ |
Sm. |
|
MiA |
121 |
165 |
286 |
|
DiA |
125 |
238 |
363 |
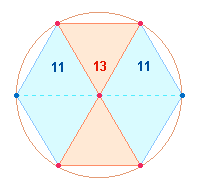
Die FS der Mittelachsen-Quadrate bilden das Verhältnis 121:165 = 11*(11:15), deren Gesamtsumme 286 und die FS 363 der Diagonalachsen-Quadrate das
Verhältnis 11*(26:33). Die Aufgliederung in 11*(13+13:11+11+11) entspricht zweimal zwei geometrischen Figuren im Hexagon aus 11 und 13 Elementen:
|
|
5.
Sowohl die ZS als auch FS aller 18 Quadrate ist also durch 7 teilbar. Die Gesamtsumme beträgt 1638+686 = 2324. Die aufeinanderfolgenden Zahlen 23+24 ergeben addiert den ZW 47 für DEUS – Gott.
6.
Daß die beiden Quadratformen, die zusammen aus 14 = 2*7 Punkten bestehen, zusammengehören, zeigt sich daran, daß
die Summen der ZW und FW entweder
getrennt oder zusammen durch 7 teilbar sind. Dies veranschaulicht
die folgende Tabelle:
RtQ+VQ
|
|||||||
|
links |
Mitte |
rechts |
Sm. |
Sm. |
|||
|
ZS |
FS |
ZS |
FS |
ZS |
FS |
ZS |
FS |
|
S |
|
|
|
|
567 |
252 |
|
|
|
|
|
|
|
|
554 |
97 |
|
|
|
|
|
|
|
517 |
337 |
|
574 |
231 |
538 |
263 |
526 |
192 |
1638 |
686 |
Die Summen
der heller unterlegten Felder sind einzeln durch 7 teilbar, die
dunkler unterlegten nur in Addition:
|
574:567 |
7*(82:81) |
7*163 |
1141 |
|
231:252 |
21*(11:12) |
21*23 |
483 |
|
805:819 |
7*(115:117) |
56*29 |
1624 |
|
554+97 |
7*93 |
21*31 |
651 |
|
517+337 |
7*122 |
14*61 |
854 |
|
1071:434 |
7*(153:62) |
35*43 |
1505 |
Die
Einzelsummen der linken Vertikale und oberen Horizontale sind durch 7 teilbar. Im Schnittpunkt dieser beiden Reihe steht der Buchstabe S mit dem ZW 18. Dieser Zahlwert entspricht den 2*9 Quadraten, die jeweils aus 1
Mittelquadrat und 8 symmetrisch gruppierten Quadraten
bestehen. Die Konstitutivzahlen 10+8 sind
Komplementärzahlen zu 1+3 und daher von trinitarischer
Bedeutung. Das Produkt 3*6 gibt den Doppelaspekt der Zahlen 1-3 als Ordinalzahlen und Kardinalzahlen wieder und entspricht den 6+3 Punkten des Tetraktysrahmens.
Erstellt:April 2008