Römischer Kalender
und Dezimalsystem
In diesem Beitrag möchte ich
einige Aspekte des römischen Kalenders und seine Beziehung zu Grundmodellen des
Dezimalsystems aufzeigen.
Als Hauptquelle
diente mir: Hans Kaletsch, Tag
und Jahr. Die Geschichte unseres Kalenders. Artemis 1970.
I.
Einleitung
II. Der
vorjulianische Kalender
d) Die Zahl 71 der Zahlenkonstruktion
Die Zahlenwerte
der republikanischen Monatsnamen
I. Einleitung
1.
Vieles
in römischer Geschichte, Kultur und Religion ist geprägt von Zahlenbedeutungen,
so auch der römische Kalender. Das Dezimalsystem hatten die Römer als Widerschein
göttlicher Wirklichkeit erkannt. Anschauung dafür war besonders der
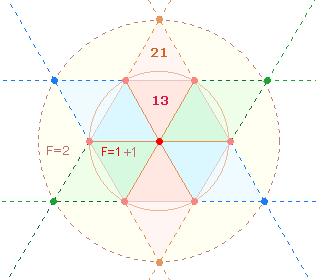
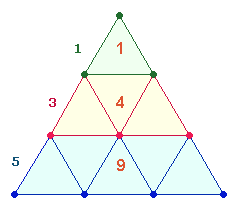
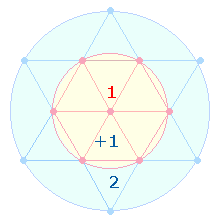
Tetraktysstern, eine Erweiterung des Hexagons. Die in beiden zu erkennenden 3 Figuren des Doppeldreiecks (13 Elemente) und der Doppelraute (21 E) interpretierten sie als Gemeinschaft
dreier Gottheiten, wie die Verehrung der obersten drei Staatsgottheiten IUPPITER
IUNO MINERVA
beweist:
|
|
Tatsächlich ist das Prinzip der vollkommenen Einheit dreier
göttlicher Personen das ideale Paradigma jeder menschlichen Gemeinschaft. Der
antike Mensch suchte seine Identität in der Teilhabe an der höchsten
Seinswirklichkeit. Wenn diese aus den geometrischen Figuren des Dezimalsystems
und in der Struktur der Zahlen selbst – vornehmlich in den Verhältnissen 1:2 und 1:3 – erkennbar war, so mußte sich der menschliche Geist zu
höchstem Bemühen angespornt fühlen, diese Wirklichkeit überall in der Schöpfung
zu entdecken und durch eigene Werke und Einrichtungen an ihr teilzuhaben. (Es
ist der neuzeitliche Mensch, der die Kostbarkeit seines geistes- und
religionsgeschichtlichen Erbes zu schätzen verlernt hat und seine Identität
lieber in den Reizen und Rätseln der Schöpfung als in der Weisheit und Liebe
des Schöpfers zu suchen scheint.)
2.
Wenn
die Schöpfung von Gott stammt, dann ist alles nach seinem eigenen Wesen
geschaffen. Die abstrakteste Manifestation ist das Dezimalsystem mit seiner
zyklischen Wiederkehr von je 10
Einheiten.
3. Die Ordnung des
vorjulianischen Kalenders richtet sich daher nach idealen Zahlenverhältnissen,
in die auch die Schaltkorrekturen einbezogen sind. Die Zahlenkonstruktion ist
so gut wie möglich zu erklären.
II. Der vorjulianische Kalender
1.
Der
vorjulianische Kalender hatte 355 Tage. Dies entspricht etwa einen dreiviertel Tag (genau: 15 Stunden, 12 Minuten) mehr als 12 synodische Mondmonate.
2.
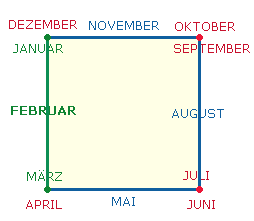
Der
römische Kalender hatte 4 Monate mit 31, 7 Monate mit 29 Tagen, der Februar hatte 28 Tage:
|
Jan. |
Febr. |
März |
April |
Mai |
Juni |
Juli |
Aug. |
Sept. |
Okt. |
Nov. |
Dez. |
|
29 |
28 |
31 |
29 |
31 |
29 |
31 |
29 |
29 |
31 |
29 |
29 |
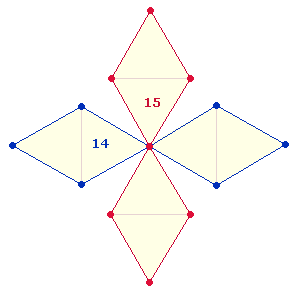
Auffällig ist die Abfolge von 29 und 31 Tagen. Die beiden Zahlen kommen
zustande durch die Verbindung zweier Doppelrauten (DR) zu einem Achsenkreuz, das zur
dreidimensionalen Figur des Oktaeders zusammengefügt werden kann. Der Rahmen einer DR besteht aus 15 Elementen. Bildet man ein DR-Kreuz, beträgt die Zahl der
Elemente 29 bei einem und 31 bei drei Mittelpunkten:
|
|
|
Die Monate Januar und Februar bilden mit 29+28 = 57 Tagen eine Einheit, was auch an lautlichen
Übereinstimmungen zu erkennen ist. Sie wurden ursprünglich an den Dezember
angehängt und erhielten Verbindungsfunktion zwischen altem und neuem Jahr. Die
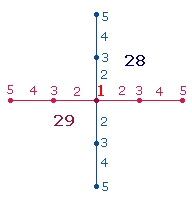
Zahl 57 kommt zustande, wenn man ein Achsenkreuz 3 (AK3) von der Mitte aus nach 4
Richtungen von 1-5
numeriert. Eine Achse kommt auf den Wert 29, die andere – ohne Mittelpunkt – auf 28:
|
|
3.
Die 10 Monate weisen zwei symmetrische
Muster auf, durch die sie in 2*5 Einheiten aufgeteilt werden:
|
Jan. |
Febr. |
März |
April |
Mai |
Juni |
Juli |
Aug. |
Sept. |
Okt. |
Nov. |
Dez. |
|
11 |
12 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
29 |
28 |
31 |
29 |
31 |
29 |
31 |
29 |
29 |
31 |
29 |
29 |
Die Monate Mai und Oktober (3 und 8) bilden mit jeweils 31 Tagen die Mitte ihrer Einheit.
Die beiden Einheiten sind den Einteilungsmöglichekeiten eines Achsenkreuzes
nachgebildet:
|
|
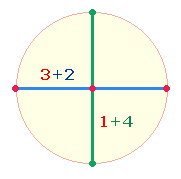
In
der Horizontalachse sind Punkte
und Linien als unterschiedliche Merkmale zusammengefaßt,
in der Vertikalachse steht der Mittelpunkt gegen 2*2 Symmetrieelemente.
Die beiden Muster lassen sich auf die
Erweiterung des Hexagons zum Tetraktysstern anwenden. Dazu ein weiterer
Beitrag.
4.
Die
Tage der ersten 5
Monate haben die Summe 151,
die der 2. Hälfte 147,
zusammen sind es 298 = 2*149 Tage. Aus 2*(9+8) Elementen besteht das Achsenkreuz
5 und eine
einzelne numerierte
Tetraktysseite.
Die Primzahl 149 zeigt in ihren Einzelziffern die Quadrierung der Zahlen 1, 2 und 3.
Die 9 Dreiecke der Tetraktys haben von
Ebene zu Ebene das Verhältnis 1:4:9. 2*149
bezieht sich dann auf zwei Tetraktys:
|
|
4.
Die
Monate Januar und Februar bilden zwar eine Einheit, sind
aber mit den übrigen Monaten durch Zweiteilung in je 6 Monate verbunden. Denn die Summe
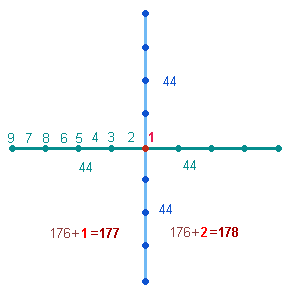
der Tage von Januar bis einschließlich Juni beträgt 177, die der zweiten Jahreshälfte 178. Damit ist die Teilung näher am
Halbierungspunkt als die Teilung der 10 Monate:
|
Jan. |
Febr. |
März |
April |
Mai |
Juni |
Juli |
Aug. |
Sept. |
Okt. |
Nov. |
Dez. |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
29 |
28 |
31 |
29 |
31 |
29 |
31 |
29 |
29 |
31 |
29 |
29 |
|
177 |
178 |
||||||||||
Rechnet man für eine Mondumlaufbahn
29,5 Tage, kommen auf die ersten 6 Monate ebenfalls 177 Tage.
Die Zahlen 177 und 178 entsprechen einer Numerierung des
Achsenkreuz 5 von 1-9, einmal mit 1, einmal mit 2 Mittelpunkten:
|
|
Auch auf die 15 Elemente des
Doppelrautenrahmens lassen sich die beiden Zahlen in ihren Einzelziffern anwenden, wenn man einmal den
Mittelpunkt verdoppelt:
|
|
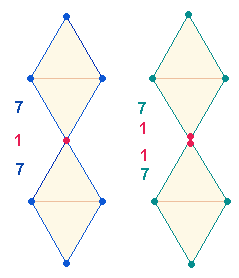
Die Faktoren der Zahl 178 sind 2*89. Die Einzelziffern
bezeichnen die 9+8 Elemente einer AK5-Achse.
Aus 8+9 Elementen besteht auch je
eine Oktaederhälfte.: 4 Punkten + 4 Linien der Mittelbasis und 1 Punkt + 4 Linien + 4 Flächen.
5.
Das
Achsenkreuz der 29+28
Tage des Januar und Februar lassen die Vermutung einer
Vierteilung des Jahres aufkommen. Tatsächlich zeigt die Anzahl der Tage der 4*3 Monate eine erstaunliche
Gleichmäßigkeit:
|
Jan. |
Febr. |
März |
April |
Mai |
Juni |
Juli |
Aug. |
Sept. |
Okt. |
Nov. |
Dez. |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
29 |
28 |
31 |
29 |
31 |
29 |
31 |
29 |
29 |
31 |
29 |
29 |
|
88 |
89 |
89 |
89 |
||||||||
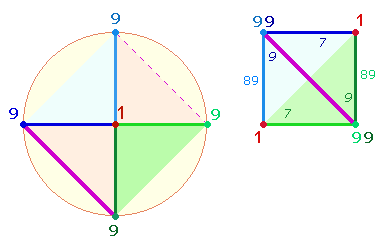
Als Modell der zweiten
Jahreshälfte ist die Quadratbildung des Achsenkreuzes AK5 anzusehen. Dabei verdoppelt sich die Zahl 1, die jeweils einen Diagonalpunkt besetzt, während sich
auf den beiden anderen Diagonalpunkten jeweils zwei Neunen vereinen. Die folgende
schematische Darstellung beschränkt sich auf die erste und letzte
Numerierungszahl:
|
|
Eine Jahreshälfte wird somit
diagonal jeweils durch 9+7 = 16 Positionen und 17 Zahlen repräsentiert, die von 1-9 und 9-2 numeriert sind.
1. Alle zwei Jahre wurde im Februar eine Schaltung vorgenommen. Im
zweiten Jahr wurden nach dem 23. 22 Tage und im vierten Jahr nach dem
24. 23 Tage eingeschoben. Danach wurden
die restlichen 5
bzw. 4 Tage angehängt.
Die Addition der beiden
Zahlenpaare beträgt 47+45 = 92.
Das Produkt 4*23
verweist wiederum auf einen Quadratrahmen aus 2 Linien und 3 Punkte je Seite.
2. Die Ordnung der Schaltungen
bewirkte, daß ein Jahr durchschnittlich ein
Tag länger war, als es Cäsars Kalenderreform entspricht. Auf diese Weise blieb
das astronomische Jahr um 1
Tag zurück.
Der 4-Jahresrhyhtmus umfaßte 1465 Tage, also vier Tage mehr als der julianische
Kalender. Davon entfielen 1192
auf die 10
Monate ab März und 273
auf die Monate Januar und Februar. Die Zahl 273 gibt durch die Produktzahlen 13*21 das Flächenverhältnis 1:3 im Doppelkreis wider (s. erste
Grafik), da 13
Elemente dem inneren Kreis der DR
angehören und die ganze DR 21 Elemente umfaßt. Außerdem sind in
den Einzelziffern von 13
und 21 die beiden
Flächenverhältnisse des Dopelkreises enthalten.
Wenn sich also der ganze Kalender so konsequent auf die
Wirklichkeit die Einheit der drei göttlichen Personen ausrichtete, würde eine
Korrektur das transzendente Zahlengebäude durcheinandergebracht haben, etwa
wenn man von 22+23 auf 20+21 Schalttage gewechselt hätte.
3.
Die Rückkehr zum Ausgangspunkt ist ein
besonderes Merkmal des Kreises. Sie zeigt sich erneut bei der ZW/FW-Verrechnung der Zahl der Tage des
4-Jahreszyklus:
|
|
ZW |
FW |
Sm. |
FW |
|
|
355 |
76 |
|
|
|
|
377 |
42 |
|
|
|
|
355 |
76 |
|
|
|
|
378 |
18 |
|
|
|
Sm. |
1465 |
212 |
1677 |
59 |
|
FW
|
298 |
57 |
355 |
76 |
|
Sm. |
|
|
|
135 |
Die
FW haben den Durchschnittswert 53, der in den Einzelziffern die
Radialelemente des Doppelkreises und das entsprechende Flächenverhältnis 3:1 darstellt. Dies gilt ebenso für
den Wert 57 in Bezug auf die 5+2 Punkte der Doppelraute.
1.
Wie
Kalendarien anderer Kulturkreise war die Absicht des vorjulianischen Kalenders,
Mond- und Sonnenjahr miteinander zu verbinden. Die Tage eines Mondumlaufs
blieben aber weiterhin Grundlage der 12 Monate eines regulären Jahres. Ob man dafür die nähere Zahl
von 354 Tagen oder die etwas ungenauere
von 355 Tagen wählte, spielt dabei keine
Rolle. Ein Vergleich mit dem griechischen Kalender zeigt die Eigenart des
römischen.
2.
Die
Griechen führten etwa zu Beginn des 6. Jahrhunderts einen Kalender mit 12-mal abwechselnd
30 und 29 Tagen und einem achtjährigem Zyklus ein. Im 3., 6. und 8.
Jahr hängten sie einen 13.
Monat an, sodaß nach 96+3
Mondumläufen das 9. Jahr wieder mit einer neuen Mondphase beginnen sollte. Sie
hatten bereits das Jahr mit 3561/4 Tagen richtig berechnet, aber die Mondumlaufbahn
um Bruchteile zu kurz eingeschätzt. Daher fand Neumond erst 1½ Tage später statt.
3.
Die
Schöpfer des römischen Kalenders verzichteten völlig auf eine Übereinstimmung
von Monatsbeginn und Mondphase. Sie hielten an 12 Monaten fest, indem sie den Monat Februar um auf 50 bzw. 51 im zweiten bzw. vierten Jahr
verlängerten.
4.
Es
ist wohl unmöglich zu eruieren, ob die Kalenderexperten die wahre Länge des
Sonnenjahres kannten und die Differenz von einem Tag je Jahr bewußt in Kauf
nahmen oder nicht.
5.
Vorausgesetzt,
die genaue Abweichung wäre bekannt gewesen, hätte man pragmatisch die
Jahresordnung aufrecht erhalten können, indem man in der entsprechenden
Jahresperiodik einmal eine Schaltung hätte entfallen lasssen, also nach jeweils
22 und 23 Jahren. In dieser Beziehung
scheint jedoch pragmatisches Vorgehen – aus welchen Gründen auch immer –
versagt zu haben. Tatsächlich wurde die Schaltung häufiger unterlassen als sie
erforderlich war.
6.
Ein
weiteres grundsätzliches Problem jedes Kalendariums besteht darin, ein
astronomisches Kalenderdatum für eine der vier Wendepunkte des Sonnenjahres
festzulegen. Solange dieses nicht nachprüfbar war und durch Rechtsbeschluß
Gültigkeit erlangt hatte, gab es keine wirkliche kalendarische Sicherheit.
d) Die Zahl 71 der Zahlenkonstruktion
1.
Die
Zahl vier des periodischen Jahreszyklus
läßt sich auf die vier
Phasen einer Mondumlaufbahn beziehen. Man kann sie durch Verhältnisse von 1:3, 2:2 und 3:1 bezeichnen.
2.
Als
geometrisches Modell eignet sich das Quadrat mit seinen 4 Seitenlängen. Eine einzelne Seitenlänge steht im Verhältnis zu den drei übrigen, indem diese durch vier Punkte begrenzt werden.
Von dieser Struktur
her versteht sich die außerordentliche Bedeutung der Zahl 71, die in 355 5-mal enthalten ist. Das Prinzip 7:1 = 3:1 ist auch auf das DR-Kreuz übertragbar. Denn der Rahmen einer der vier Raute besteht aus 4 Linien, 3 Punkten und dem Mittelpunkt.
3.
Verständlich
wird diese Parallele, wenn man den Zahlen 17 und 71
deren komplementäre Entsprechungen 93 und 39
zur Seite stellt. Ihre Faktoren 31 und 13
lassen sich als Verhältniswerte auffassen. Der jeweilige Faktor 3 bedeutet für die vier Seiten des Quadrats jeweils 1 Linie und 2 Begrenzungspunkte und für den
Kalender 3 Monate.
Da der DR-Stern 3 DR enthält, sind 3 Paarungen denkbar, die der
Bildung eines Oktaeders dienen. Aus 13 Punkten besteht ein DR-Kreuz und aus 31 Elementen der Rahmen eines der beiden DR-Kreuze (s.oben).
4.
Bei
einem Mittelpunkt besteht ein DR-Rahmen
aus 29 Elementen, denen die 8 Elemente des Quadrats hinzufügen
sind. Zusammengesetzt ergibt sich daraus die Zahl 298, die oben bereits besprochen
wurde.
Die Primfaktoren der
1465 Tage des 4-Jahreszyklus sind 5*293, sie ergeben wiederum den FW 298. Die Zahl 293 ist aufteilbar in 29 und 3 und bezeichnet dann drei DR-Kreuze.
5.
Wenn
man das Prinzip 1:3 auf die Zahl der Elemente des
Quadrats und des DR-Kreuzes überträgt und wiederum zusammensetzt, erhält man 1+8 und 7+21 = 928 und in der Umkehrung 289.
Wie verwandt beide Zahlenpaare
sind, zeigt die Addition der Zahlensummen (ZS) und Faktorensummen (FS):
|
|
|
|
Sm. |
|
|
Sm. |
GS |
Fkt. |
|
ZW |
289 |
928 |
1217 |
298 |
829 |
1127 |
2344 |
8*293 |
|
FW |
39 |
73 |
151 |
829 |
980 |
1053 |
81*13 |
|
|
|
|
|
1290 |
|
|
2107 |
|
|
|
980:1127 = 49*(20:23) = 7*7*43 |
||||||||
|
1290:2107 = 43*(30:49) |
||||||||
Das erste auffällige
Ergebnis ist, daß die ZS 2344
wie der 4-Jahreszyklus des Kalenders durch 293 teilbar ist, das zweite, daß die ZS+FS beider Zahlenpaare den gemeinsamen
Teiler 43
enthält. Die Zahl 43 ist
auf Quadrat, Tetraktys und Doppelraute und schließlich auf die Unterteilung des
Jahres in 4*3 Monate.
6.
Das
Verhältnis 1:3
bestätigt sich in der Zahl der Tage der 4*3
Monate: 88 89 89 89.
Der FW der Zahl 88 ist 17, die Umkehrung der Zahl 71. Daher ist die FS dieser Jahresunterteilung 284 = 4*71. Das Differenzverhältnis lautet
daher 71*(4:1).
Der
Februar ist der Ausnahmemonat. Die Zahl seiner Tage ist gerade und die
Schaltungen werden ihm eingefügt. Er ist die Schaltstelle zwischen altem und
neuem Jahr. Er ist einerseits 2.
Monat, andererseits 12.
Monat, da ursprünglich das Jahr mit dem März begann. Die Zusammensetzung der
beiden Zahlen zu 212
könnte die Anordnung der 12
Monate auf den vier Seiten des Quadratrahmens charakterisieren, da auf jeden
Punkt zwei Monate und je Linie ein Monat kommen:
|
|
7.
Der
Monat Februar vertritt das Verhältnis 3:1, wenn man die ZS+FS der einzelnen Jahre des
4-Jahreszyklus ermittelt, der in 2*2
Jahre unterteilt werden soll:
|
|
ZW |
FW |
Sm. |
|
ZW |
FW |
Sm. |
GS |
|
J 1 |
28 |
11 |
|
J 3 |
28 |
11 |
|
|
|
J 2 |
50 |
12 |
|
J 4 |
51 |
20 |
|
|
|
Sm. |
78 |
23 |
101 |
|
79 |
31 |
110 |
211 |
Die Einzelergebnisse 101
und 110 stellen Umkehrwerte
dar, wenn man sie zusammengesetzt denkt aus 10+1 und 1+10. Sie bedeuten jeweils 10 Maßeinheiten, die durch 11 Begrenzungspunkte abgeteilt sind.
Sie sind jeweils auf eine einzelne Raute beziehbar aus 11 Elementen, wobei eines den
Mittelpunkt darstellt.
Die
Einzelziffern der Primzahl 211
entsprechen den Flächengrößen des Doppelkreises des Tetraktyssterns: die
Unterteilung des äußeren Kreises in 2+1 Flächeneinheiten und 1 Flächeneinheit für den
inneren Kreis:
|
|
8. Die ZS+FS der übrigen Monate sind jeweils 4*(355-28) = 4*327 = 1308. Die FS des Februar beträgt 54. Das Gesamtergebnis ist daher 1465+1362 = 2827 = 11*257.
Die beiden angrenzenden Zahlen 28
und 27 sind konstitutiv für
ihre Summe 55,
die sich aus der Addition der Zahlen von 1-10
ergibt und somit das Dezimalsystem manifestiert.
Die
ZS+FS der 5 Monate der Februarseite steht in
folgendem Verhältnis zu der der übrigen 7
Monate: 1155:1672 = 11*(105:152).
Die FW der Zahlen 105 und 152 sind 15 und 25 und verweisen auf die Achsenkreuznumerierung der Punkte allein und der Punkte
und Linien zusammen. Die ZW/FW-Verrechnung ergibt:
|
|
ZW |
FW |
Sm. |
|
|
1155 |
26 |
|
|
|
1672 |
36 |
|
|
Sm. |
2827 |
62 |
|
|
FW |
268 |
33 |
301 |
Die
Zahl 301 kann ebenfalls im
Sinne eines Verhältnisses 3:1
verstanden werden. 5:7
Punkte der Doppelraute entsprechen 1:3 Flächeneinheiten des
Doppelkreises.
9. Die ZS+FS eines Regeljahres ist 355+338 = 693 = 11*63.
Dies entspricht der dreifachen Summe der Zahlen 1-21 und verweist sowohl auf die drei
Doppelrauten des Tetraktyssterns als auch auf den ZW des Namenscodes VESTA.
Bemerkenswert ist die ZW/FW-Verrechnung der ZS+FS aller 4 einzelnen Jahre einer
Kalenderperiode:
|
Jahr |
1. |
2. |
3. |
4. |
Sm. |
FW |
Sm. |
FW |
|
ZFS |
693 |
716 |
693 |
725 |
2827 |
268 |
|
|
|
FW |
24 |
183 |
24 |
39 |
270 |
16 |
|
|
|
Sm. |
717 |
899 |
717 |
764 |
3097 |
284 |
3381 |
40 |
|
FW |
3097 = 19*163 |
182 |
75 |
257 |
257 |
|||
|
Sm. |
|
|
|
|
|
|
|
297 |
Das erste Ergebnis 284 ist durch 71 teilbar, das zweite 257 ist wiederum der Faktor der ZS+FS 2827. Die Konstitutiven 129+128 der Zahl 257 verbinden durch 12+9 und 12+8 Tetraktys und Doppelraute
einerseits und den Quadratrahmen andererseits. Ihre FS 46+14 = 60 zu 257 hinzugefügt, ergibt die Primzahl 317, die die Komponenten für die Zahl
71 enthält: 3*17 + 3+17 = 71.
Die addierten Werte der beiden
Schaltjahre sind ebenfalls durch 11
teilbar: 1441 = 11*131. Das Verhältnis 1:3/3:1 wird darin sichtbar.
e) Theorie und Praxis
1.
Der
vorjulianische Kalender geht auf das 7.-6. Jh. v.Chr. zurück. Nach antiken
Quellen soll er von König NVMA POMPILIVS, dem Nachfolger des Romulus,
eingeführt worden sein. Seine Schöpfer hatten das ehrgeizige Ziel, die
Mondphasen mit dem Sonnenjahr zu verbinden.
2.
Theoretisch
begann ein Monat mit einer neuen Mondphase. Der erste Tag des Monats hieß Kalendae von calare – ausrufen, da er öffentlich bekanntgemacht
wurde. Dies könnte vor der Konstruktion des Kalenders üblich gewesen sein und
wurde als Traditionsgrundlage übernommen.
3.
Wie
ich in der bisherigen Darlegung zu zeigen versuchte, waren die Schöpfer des
Kalenders darauf bedacht, eine Zahlenkonstruktion von größtmöglicher
Vollkommenheit hervorzubringen. Sie hielten offensichtlich die göttlichen
Gesetze der Zahlenordnung für eine bedeutendere Wirklichkeit als die
physikalischen Gesetze des Geschaffenen.
Wir
würden gerne wissen, wie die Erfinder des Kalenders über seine astronomische
Genauigkeit dachten. Außer dem regulären Schaltzyklus hinaus scheinen sie keine
weiteren Verfügungen hinterlassen zu haben. Jedenfalls war der Einhaltungsmodus
des Kalenders nicht an eine religiös-rechtliche Ebene geknüpft.
4.
Es
erscheint als ein Rätsel, warum die ordnungsgewohnten Römer so wenig Wert auf
astronomische Genauigkeit legten. Nachdem klar geworden war, daß der
Schaltzyklus nicht die gewünschte Übereinstimmung mit dem Sonnenjahr bewirkte,
wurden sogar die Schaltungen selbst als etwas Irreguläres empfunden und seit
dem zweiten Punischen Krieg nicht mehr regelmäßig eingehalten. Im Jahr 190
v.Chr. beispielsweise war der Kalender dem Sonnenjahr 119 Tage voraus und Cäsar schaltete
im Jahr 46 v.Chr. 90
Tage ein.
5.
Zuständig
für die Regulierung des Kalenders waren das Collegium Pontificum – das Kollegium der Oberpriester (16 an der Zahl zur Zeit Caesars). Die pontifices hatten beratende Funktion in
allen religiösen Angelegenheiten. Cicero urteilt in de legibus 2,12,29, die Einschiebung von
Schalttagen sei von Numa mit Sachkenntnis eingeführt, aber später durch die
Nachlässigkeit der Oberpriester zunichte gemacht worden:
...ratio intercalandi, quod institutum perite a Numa, posteriorum
pontificum neglegentia dissolutum est.
6.
Über
die Gründe dieser Nachlässigkeit kann man nur spekulieren:
–
Wie
schon erwähnt, war der Kalender keine religiös-rechtliche Institution.
–
Die
Einschiebung der vorgesehenen Schalttage wurde als eine Art Notlösung
empfunden, die reguläre Ordnung der Monate wurde als eigentlich normativ
angesehen und besaß überkommene Autorität. Man unterließ lieber eine Schaltung
als ständig aufs Geratewohl zu korrigieren. Die Ausrichtung nach einem
astronomischen Fixpunkt war unbekannt.
–
Man
wagte nicht, eindeutige astronomische Kriterien für die Regulierung des
Kalenders zu erforschen und sie institutionell zu verankern. Erstens besaß man
zu wenig Sicherheit über die Länge des Sonnenjahres, zweitens hätte man ein
sinnvolles Zahlenwerk schaffen müssen. Drittens vertraute man prinzipiell den
überlieferten Normen als MOS MAIORUM – Sitte der Vorfahren.
–
Die
von Cicero gerügte Nachlässigkeit der pontifices ist auch ein Indiz dafür, daß der Römer sein
Selbstverständnis nicht strikt an Naturerscheinungen binden wollte. Er sah
offensichtlich in einer Optimierung des Kalenders nicht den vordringlichen
Willen der Götter.
–
Verbindlichkeit
besaßen die religiösen Feste. Sie waren jedoch nicht – wie auch Teile des
christlichen Kirchenjahres – an astronomische Fixpunkte gebunden.
Insgesamt zeigt sich
das unlösbare Dilemma, eine ideale Ordnung für eine davon unabhängige
physikalische Wirklichkeit nutzbar zu machen. Der Kalender stellte ein
Zahlenideal dar, das in sich einen gültigen Wert und normative Bedeutung für
römisches Bewußtsein und Selbstverständnis besaß.
7.
Andererseits
darf man tiefere Einsichten nicht ausschließen. Vielleicht hatte man erkannt,
daß die genaue Jahreslänge nicht vollkommen regulierbar war und wollte dann
wenigsten einen vollkommenen Annäherungswert schaffen. Die zugrundeliegenden
Zahlenspekulationen und Berechnungen waren aber so komplex, daß in der
Folgezeit wohl nur wenige Menschen sich die Mühe machten, dieses Wissen immer
wieder neu zu erarbeiten.
Ich möchte daher in einem weiteren
Ansatz eine Vermutung über die wesentliche Idee der Kalenderkonstruktion in
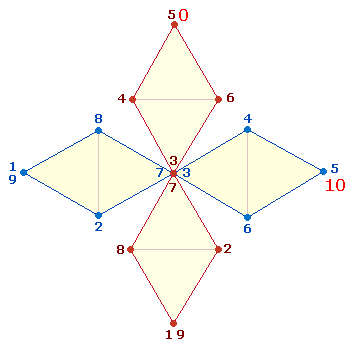
knaper Form anstellen: Die Grundzahlen von 1-9 und die Zahlen 1-10 sind im folgenden Doppelrauten-Kreuz vereinigt:
|
|
Wenn
das DR-Kreuz zu einem Oktaeder zusammengefügt wird, entfällt durch Vereinigung
von zweimal zwei Punkten jeweils ein Punkt und jede DR besteht aus 20 Elementen. Zählt man die beiden
Nullen als zahlenrelevant, erhält man die Zahl 21. Die gesamte Konstruktion besteht dann aus den Zahlen 40+21 = 61. Das römische Durchschnittsjahr
des Vierjahreszyklus hat 366 = 61*6 Tage. Die Einzelziffern des Produkts lassen sich auf die 13 Punkte des Tetraktyssterns und
seiner beiden konzentrischen Kreise beziehen.
Die ZW/FW-Verrechnung führt zu weiteren relevanten
Ergebnissen:
|
|
ZW |
FW |
Sm. |
FW |
Sm. |
|
|
40 |
11 |
|
|
|
|
|
21 |
10 |
|
|
|
|
Sm. |
61 |
21 |
82 |
43 |
|
|
FW |
61 |
10 |
71 |
71 |
|
|
Sm. |
|
|
153 |
114 |
|
|
FW |
|
|
23 |
24 |
47 |
Das
erste Verrechnungsergebnis 71 ist maßgebender Faktor des
Regeljahres von 355
Tagen. Die Addition der Einerstellen der Produkte 5*71 und 6*61 ergibt 5+6 = 11 und stellt die Differenz zwischen
355 und 366 dar.
Die
Zahlen 23 und 24 können den Anstoß gegeben haben,
die Schaltungen nach diesen Tagen einzufügen.
Erstellt: März 2007
Überarbeitet: Mai/Juni 2008