ORANDUM EST UT SIT MENS SANA IN
CORPORE SANO
(Umkehrungen von 736)
In dieser Untersuchung geht es besonders um die Zahlen
1269 und 2169.
1.
In Teil 1 wurden die Zahlensummen (ZS) und die Faktorensummen
(FS) der Verszeile ohne und mit den
Elisionen E und A
ermittelt:
Die Zahlen 381 und 382 bilden die
konzentrische Mitte der Summe 763 = 7*109.
Die ZW/FW-Verrechnung
liefert folgendes Ergebnis:
|
|
|
|
|
|
sm |
FW |
sm |
FW |
sm |
|
ZS/FS |
321 |
327 |
436 |
442 |
1526 |
118 |
|
|
|
|
FW |
110 |
112 |
113 |
32 |
367 |
367 |
|
|
|
|
sm |
|
|
|
3*631 |
1893 |
485 |
|
|
|
|
FW |
|
|
|
|
634 |
102 |
736 |
33 |
23*32 |
2.
Die
auftretenden Umkehrformen 367 und 736 legen die Vermutung nahe, daß die Einzelziffern
dieser Zahlen zur gematrischen Konzeption der Verszeile
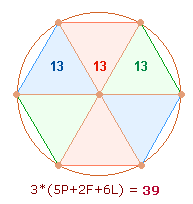
gehören. In erster Linie ist wohl an 3*(6+7)
und zwei Modelle zu denken. Das erste betrifft das sanduhrförmige Doppeldreieck
des Hexagons:
|
|
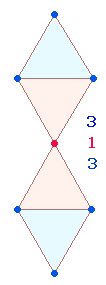
Ein solches Doppeldreieck bildet auch die Mitte einer von drei
Doppelrauten:
|
|
Die Quersumme 16
der Einzelziffern 3+6+7 ist die Summe der
Zahlen 1-3
und 1-4.
Die Zahlen 3 und 4
sind ein wesentliches Thema der gematrischen Konstruktion der Verszeile.
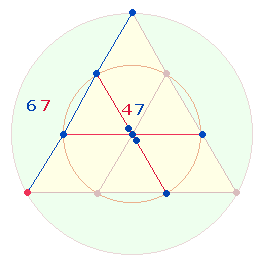
Als zweites Modell ist der Tetraktysrahmen anzusehen. Die Elemente
einer einzelnen Seite bestehen aus 3 Linien + 4 Punkten, alle drei Seiten jedoch aus 3*(3+3) = 18
Elementen. Diesen Doppelaspekt kann man zu 3*67 zusammenfassen:
|
|
3.
Einen weiteren
Einblick in die gematrische Konzeption kann die ZS+FS der 6
Umkehrungen geben:
|
Zahl |
367 |
673 |
637 |
376 |
736 |
763 |
3552 |
|
FW |
367 |
673 |
27 |
53 |
33 |
116 |
1269 |
|
sm |
1677 = 129*13 |
1875 = 3*625 |
4821 |
||||
|
1269 = 3³*47 > 56 |
|||||||
Die Einzelergebnisse weisen auf die genannten
geometrischen Modelle hin. Die Zahl 625 = 25²
gibt in den Einzelziffern die Elemente des Doppeldreiecks wieder: 6 Linien, 2 Dreiecksflächen,
5 Punkte.
4.
Die FS 1269
erweckt deswegen besondere Aufmerksamkeit, weil die 4Werte
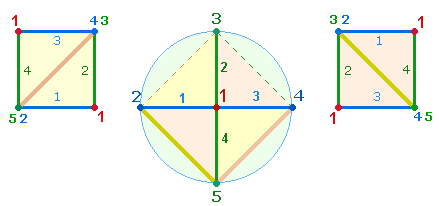
der doppelten Zählung des Verses 2169 ist. Die Teilung der beiden Summen durch 9 ergibt 141 und 241. Beide Ergebnisse lenken jedoch den Blick auf
die Quadratbildung durch das numerierte Achsenkreuz, im ersteren Fall mit
Numerierung der Punkte, im letzteren mit zusätzlicher Numerierung der Linien:
|
|
Der Mittelpunkt 1 und die übrige Numerierungssumme
lassen sich zusammensetzen zu 14-1 und 24-1. Bei der Quadratbildung kommt eine zweite 1
hinzu, die Numerierungssummen sind dann 14-2
und 24-2, zusammen 15+16
= 31 und 25+26 = 51.
Die Relevanz des einfachen Achsenkreuzes zum
Dezimalsystem besteht darin, daß jede Achse aus 5 Elementen besteht, das
Achsenkreuz als ganzes jedoch aus 9 Elementen. Daraus ergibt die Formel 10+9, die durch 109
in den ZS und FS
des Verses verwirklicht ist. Teilt man die beiden vierstelligen Zahlen in
zweistellige auf, ergibt die Addition 12+69 = 81
und 21+69 = 90. Das Verhältnis der beiden
Summen ist 9*(9:10) und erfüllt
damit den Doppelaspekt der Achsenkreuzelemente. Dasselbe gilt für 90 = 9*10
allein.
5.
Die ZW/FW-Verrechnung verweist auf das SATOR-Quadrat
mit der ZS 303:
|
|
|
|
sm |
FW |
|
ZS/FS |
1269 |
2169 |
3438 |
199 |
|
FW |
56 |
247 |
303 |
104 |
|
sm |
|
|
|
303 |
Erstellt: März 2011