Das Geheimnis der 7
römischen Zahlzeichen und der 14 übrigen Buchstaben
und ihre
Beziehung zum Dezimalsystem
Die Verteilung der
römischen Zahlzeichen im Alphabet sowie ihre Bedeutung erscheinen willkürlich.
In Wirklichkeit stellt ihr Verhältnis zu den übrigen Buchstaben eine
unübertreffliche Ordnung dar, wie im Folgenden aufgezeigt werden soll. Dieses
komplexe Thema zu verstehen, erfordert vom Leser ein erhebliches Maß an Geduld
und Ausdauer. Denn in der Ordnung des Alphabets manifestiert sich das geballte
Zahlenwissen der Römer. Zu ihrem mathematischen Denken gehört die Einbeziehung
der Primzahlfaktoren, ein Verfahren, das heutiger
Mathematik unbekannt ist.
Wer über
die Lösung des Geheimnisses eine schnelle Auskunft möchte, findet sie im dritten Teil der Untersuchung. Eine weitere Zusammenfassung folgt am Ende des vierten und
letzten Teils.
Die Aufgabenstellung ist folgende:
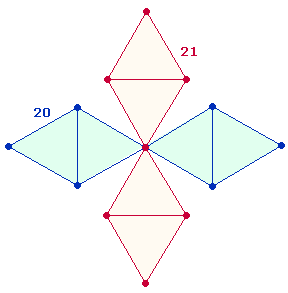
Das lateinische Alphabet mit seinen 21 Buchstaben ist gleichzeitig Modell göttlicher Ordnung. Daher
hat jeder Buchstabe einen Zahlenwert gemäß seinem Platz im Alphabet. 80 beträgt die Summe der 7
Zahlzeichen, 151 die der übrigen 14 Buchstaben. Es zeigt sich, daß an dieser Einteilung
auch die Umkehrzahlen 115 und 511
beteiligt sind. Die gesamte Untersuchung dient der logischen Verknüpfung dieser
Zahlengrundlage.
A. ENTWICKLUNGEN
I. Römische Zahlzeichen und ihre Werte
II. Der Bezug der ZZ zum Tetraktysstern und seinen Figuren
a) Tetraktysstern,
Tetraktys, Hexagon
s.a. Die Buchstaben und Zahlzeichen IV
I. Römische Zahlzeichen und ihre Werte
1.
Zum Zählen und Rechnen benutzten die
Römer 7 von 21 Buchstaben, das bedeutet das
Verhältnis 1:2 für die Teilmengen 7:14 und das Verhältnis 1:3 für die Teilmenge 7 zur Gesamtzahl 21.
Die römischen Zahlen wurden erst im ausgehenden
Mittelalter vom arabischen Zahlsystem abgelöst.
2.
Die 7 Zahleneinheiten des römischen Systems sind in
aufsteigender Reihe den folgenden Buchstaben zugeordnet:
|
1 |
5 |
10 |
50 |
100 |
500 |
1000 |
|
I |
V |
X |
L |
C |
D |
M |
3.
Wenn man die 21 Buchstaben in 3*7 Einheiten aufteilt, sind die 7 römischen Zahlzeichen (ZZ) im Verhältnis 2:3:2 angeordnet. Jeder
Buchstabe erhält die Zahl seiner alphabetischen Reihenfolge:
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
V |
X |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
Die Zahlenwerte (ZW)
der 7 römischen Zahlzeichen
ergeben addiert 80. Das Verhältnis der 4
äußeren ZW zu den 3 inneren beträgt 48:32 = 16*(2:3). Ordnet man die 4 äußeren ZZ
einander konzentrisch zu und setzt die Paare CX ins erste und DV
ins letzte Drittel, erhält man für jedes Paar den ZW
24 und das neue Verhältnis 8*(3:4:3).
Die 3 Zahlzeichen VLD mit der Ziffer 5 an erster Stelle haben zu den 4 Zahlzeichen
IXCM das ZW-Verhältnis 35:45 = 5*(7:9).
4. Eine wichtige Rolle spielen auch die Faktorenwerte (FW) und ihr Verhältnis zu den ZW:
|
ZZ |
C |
D |
I |
L |
M |
V |
X |
|
|
ZW |
3 |
4 |
9 |
11 |
12 |
20 |
21 |
80 |
|
FW |
3 |
4 |
6 |
11 |
7 |
9 |
10 |
50 |
Das inklusive Faktorensumme- (FS) zu Zahlensumme (ZS)-
Verhältnis ist 10*(5:3), das
exklusive 10*(5:8).
Die ZS von zwei ZZ ergibt den ZW
eines dritten ZZ: MI=X entspricht 12+9 = 21.
Ihre ZS+FS
ist 42+23 = 65, die Hälfte von 130.
5. Auffällig ist
die Aufeinanderfolge der ZZ in einzelnen Paaren: (Aus zwei benachbarten Zahlen konstituiert
sich jeweils die Zahl des Additionsergebnisses; gerade Zahlen bestehen aus 2
Zahlen, die durch eine mittlere getrennt sind.) Da die Zahl 11 (L) die Mitte zwischen 1 und 21 darstellt,
verbindet sie sich sowohl mit dem I als auch dem
M.
II. Der Bezug der römischen Zahlzeichen zum
Tetraktysstern und seinen Figuren
Die Bedeutung des
Tetraktyssterns habe ich unter dem Titel Entwicklung des Dezimalsystems behandelt. Unter dem
Begriff "Elemente" (E) bezeichne ich Punkte, Linien und Flächen einer geometrischen Figur oder Einteilung.
|
|
II.a) Tetraktysstern, Tetraktys, Hexagon
1.
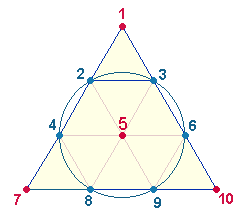
Die 7 ZZ stehen in vielfältiger
Beziehung zu den geometrischen Figuren des Tetraktyssterns, dessen zwei
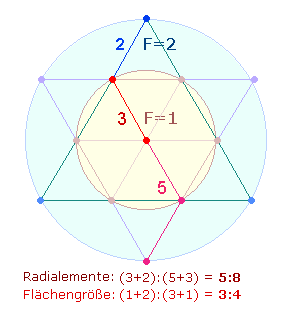
konzentrische Kreise das Flächenverhältnis 1:3 aufweisen. Die FS+ZS 50+80 entsprechen vorstehender Grafik: Das Verhältnis der FS:ZS läßt sich durch 2*5*(5:8) darstellen. Der Doppelkreis besteht
aus 2*5 Radialelementen. 5 Radialelemente sind mit der Flächengröße 3 gleichzusetzen, 3
Radialelemente mit der Flächengröße
1. Das Verhältnis 5:8 bezeichnet dann 3+(3+1)
= 7 Flächeneinheiten.
Die FS 50 beansprucht 5 von 8 Teilen der ZS 80, es bleiben also noch 3 übrig. Das Differenzverhältnis zwischen FS und ZS ist also 5:3. Durch dieses Verhältnis werden 3+1 = 4 Flächeneinheiten wiedergegeben.
Das Verhältnis 4:7 ist grundgelegt im Verhältnis der Umkehrzahlen 12:21 = 3*(4:7). Zwischen 11 und 99 gibt es 36 Umkehrzahlen-Paare,
die alle zusammengenommen dasselbe Verhältnis 4:7 mit dem gemeinsamen Teiler 396 = 36*11. (Die Formel dafür sollte gefunden werden.)
Ob der gemeinsame Teiler 2*5 in die Verhältnisrechnung einzubeziehen
ist oder nicht, soll hier nicht untersucht werden und soll offen bleiben.
Auch die ZS+FS der Zahlen 14-18 beträgt 80+50, so daß sich die Frage stellt, ob diese Zahlengruppe nicht das Modell für
die Auswahl der römischen Zahlzeichen geliefert hat.
2.
Entsprechend der Zahlensumme 80 = 2*5*(5+3) der 7
römischen Zahlzeichen besteht der Tetraktysstern aus 2*5 Radialelementen. Die 5+3 Radialelemente des äußeren und inneren Kreises stehen für die
Flächengrößen 1+3 und entsprechen dem inklusiven FS:ZS-Verhältnis 5:3, während das
exklusive FS:ZS-Verhältnis 5:8 die Flächengrößen 3+4
darstellt. Aus beiden Verhältnissen ergibt sich das vereinte Verhältnis 4:7,
das seine Grundlage im Verhältnis 12:21 hat.
Die oben erwähnten ZZ-Paare CX und
DV mit der gleichen Summe 24
spiegeln die Parität der Elemente des inneren Kreises
und äußeren Kreisrings
wider. (Weist
man jeder Einheit einen Mittelpunkt zu erhält man 2*25 = 50.) Sie haben auch die gleiche FS 13. Die ZS+FS betragen nun
zweimal 37 und weisen einerseits auf die 37 Elemente der
Tetraktys. Andererseits läßt sich die Zahl 24 auch als 2+4 Radiallinien verstehen, die für den inneren und äußeren
Kreis die Flächengröße 1 und
3 wiedergeben.
3.
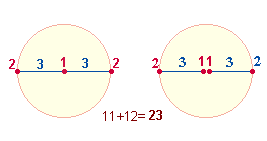
Die in den ZW der Buchstaben C und D angedeuteten Flächeninhalte 3+4 können auch mit den 5+4 Durchmesserelementen des inneren und äußeren Kreises in Beziehung gesetzt
werden. Die Rechnung lautet demgemäß 9+(5+9) = 23. Die Zahl 23 setzt sich aus den ZW der Buchstaben LM zusammen und zeigt
in seinen Einzelziffern 2 und 3 sowohl die 5 DM-Elemente des inneren Kreises als
auch die Radialelemente 2+3 des äußeren Kreisrings und inneren Kreises mit dem Flächenverhältnis 2:1. (Die Hinzunahme
der beiden griechischen Buchstaben Y und Z ist von
dieser Perspektive aus gesehen sinnvoll.) Hierin zeigt sich eine
Zusammengehörigkeit der Zahlzeichen CD-LM.
4.
Die TETRAKTYS hat zu den 3*7 = 21 lateinischen Buchstaben einen
dreifachen Bezug:
–
Sie enthält 3 Eckpunkte + 7 Hexagonalpunkte;
–
sie besteht aus 37 Elementen: 10 Punkten (P)
+ 9 Dreiecksflächen (F)
und 18 Linien (L).
–
Eine einzelne
Tetraktysseite besteht aus 3 Elementen des
Hexagonrahmens (PLP) und 2*2
Erweiterungselementen (LP). Dieser Gliederung entspricht die Aufteilung der 7 ZZ in 2+3+2 auf die 3
Einheiten von je 7 Buchstaben. Der Tetraktysrahmen setzt sich also aus 3*7 = 21
Elementen zusammen:
|
|
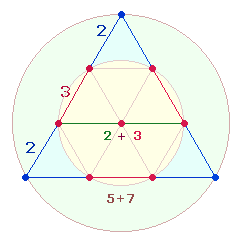
5. Vorstehende Grafik zeigt 5+7 Elemente: 2+3 und 3+4. Durch die folgende Doppelnumerierung der DM- und Radialelemente wird aus 2+3 die zweistellige Zahl 23:
|
|
Auch in dieser Doppelnumerierung kann man die Zahlzeichen LM erkennen. Zusammen mit dem Zahlzeichen I aus der mittleren 7-er
Einheit ist die ZS+FS
32+24 =56 = 8*(4+3)
entsprechend den 5 DM- und 6 Radialelementen. Die 4
übrigen Zahlzeichen haben die ZS+FS 48+26 = 74. Auch die Zahlen 7+4 geben den Doppelaspekt von 5 DM- und 6
Radialelementen wieder durch 7 Punkte und 4 Linien.
6. Durch Hinzufügung des ZW 9 des Buchstabens I wird aus dem ZW 23 der Buchstaben LM die Umkehrzahl 32. Die beiden Umkehrzahlen erhält man, wenn man die Eckpunkte+Mittelpunkt (23) der numerierten Tetraktys sowie
die 6 Hexagonalpunkte (32) zusammenrechnet:
|
|
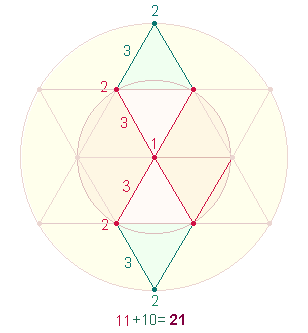
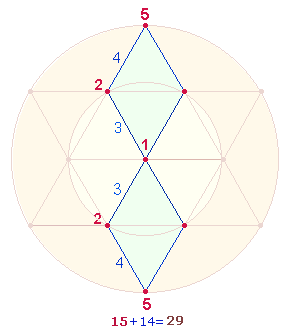
7. Die ZW der Buchstaben I-V-X (9-20-21) ermöglichen eine doppelte Numerierungsweise der 9 DM-Elemente des Tetraktyssterns: Die
eine Numerierung beschränkt sich auf die Zahlen 1, 2, 3 und ergibt 21, die zweite besetzt die
Erweiterungselmente des Tetraktyssterns mit 4 und 5 und erreicht
so das Ergebnis 29:
|
|
|
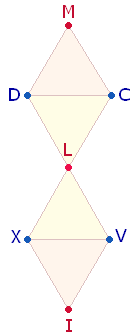
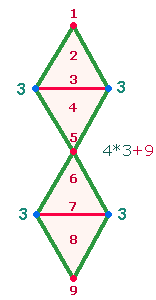
1. Die Doppelraute (DR) hat einen Rahmen aus 7 Punkten und 8 Linien und umschließt 2*3 Elemente (FLF). Sieht man die 9 DM-Elemente als
Mittelvertikale, so kommen zu den 2*3 Elementen noch 3 Schnittpunkte an den Enden und der Mitte hinzu. Es bleiben übrig 4*3 Elemente des Rahmens aus LPL. Auf diese Weise wiederholt sich die
Gleichung 12+9 = 21, die den Tetraktysrahmen mit 4*3 P + 3*3 L kennzeichnet:
|
|
2. Die Gleichung 12+9 = 21 (M+I=X) bedeutet 2*21 = 42. Wenn zwei DR in der Mittelachse und
um die Enden vereint werden, ensteht die dreidimensionale Figur des Oktaeder. Tatsächlich könnte
das Partizip Perfekt MIXT- von miscere – mischen, vereinigen einen Hinweis auf diesen Zusammenhang geben. Die Paarung VX stellt ein DR-Kreuz aus 20+1+20 = 41 Elementen dar:
|
|
Erstellt: Februar
2007