ROMA: gematrische Werte

ROMA

3:1 und 1:3 Punkte repräsentieren ebensolche Kreisflächenverhältnisse, die als geometrische Abbildung göttlicher Trinität in ROMA enthalten sind

1. Das Wort ROMA hat folgende Zahlenwerte (ZW) und Faktorenwerte (FW):

	R	O	sm	M	A	sm	GS	FW	4WS
ZW	17	14	31	12	1	13	44	15	59
FW	17	9	26	7	1	8	34	19	53
sm	34	23	57	19	2	21	78	34	112
57:21 = 3*(19:7)

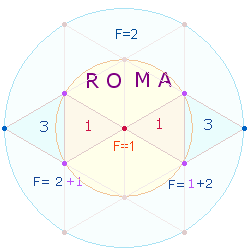
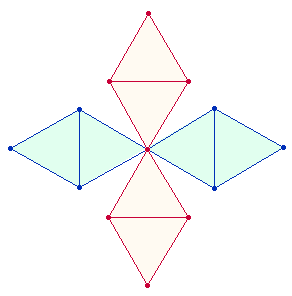
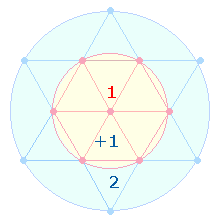
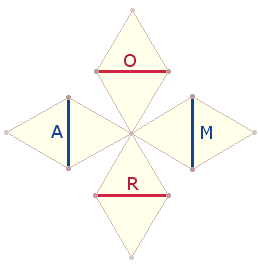
ROMA, der Mittelpunkt des römischen Reiches, ist, wie sich erweist, gematrisch auf das Endziel des Tetraktyssterns ausgerichtet: auf den OKTAEDER, dessen äußerer Aufbau sich durch ein Achsenkreuz aus vier Rauten zusammenfügen läßt, von denen jede einzelne aus 11 Elementen besteht:

Die Zahlensumme (ZS) 44 von ROMA entspricht den Elementen von vier Rauten. Bei Zählung eines einzigen Mittelpunktes reduziert sich die Zahl der Elemente von 44 auf 41.

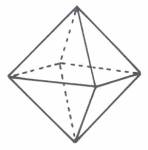
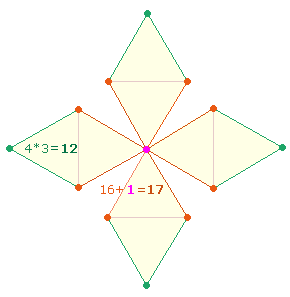
2. Ein Oktaeder besteht – ohne Volumen – aus 6 Ecken, 12 Kanten und 8 Flächen, zusammen aus 26 Elementen:

Ein Oktaeder hat die Form zweier entgegengesetzter Pyramiden mit einer gemeinsamen quadratischen Mittelbasis aus 4 Ecken und 4 Kanten = 8 Elementen. Ein paramidaler Aufbau besteht aus 4 Kanten, 4 Flächen und 1 Ecke = 9 Elementen. Somit ergeben sich für eine Paramide 8+9 = 17 Elemente aus 5 Ecken, 8 Kanten und 4 Flächen. Es bleiben 9 Elemente für den zweiten pyramidalen Aufbau übrig. Diese Aufteilung der 26 Elemente zeigt die FS 17+9 = 26 der Silbe RO. Die FS 8 der Silbe MA liefert ein zweites Mal die 8 Elemente der quadratischen Basis für die zweite Pyramide.

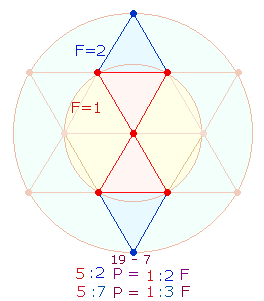
Die ZS+FS 78 = 3*26 von ROMA entspricht den Elementen von drei Oktaedern. Diese Zahl ist darin begründet, daß der Tetraktysstern drei Doppelrauten (DR) enthält und jede zweimal mit den anderen beiden ein DR-Kreuz bildet, so daß sich drei DR-Kreuze ergeben. Das Verhältnis 19:7 ist eine Umkehrung zu 17+9. Dieses Verhältnis stellt eine Entsprechung von 5+2 und 5+7 DR-Punkten zu 1+2 und 1+3 Kreisflächeneinheiten dar:

3. Die 4W-Summen 53 und 59 sind Primzahlen in der Mittelachse der 9 Zehnereinheiten von 11 bis 100:

1. E.			2. E.			3. E.
1.R.	MR	3.R.	1.R.	MR	3.R.	1.R.	MR	3.R.
11		31	41		61	71		x
13	23		43	53		73	83
17		37	47		67	x		97
19	29		x	59		79	89
1	2	3	4	5	6	7	8	9

Die Einzelziffern der beiden Primzahlen sind als Radial- und Durchmesserelemente der beiden konzentrischen Tetraktyskreise zu verstehen:

Auf diese Weise führen die Kreisflächenverhältnisse 3:1 und 1:3 in zweistelliger Zusammensetzung zu den ZS 31 und 13 der beiden Silben von ROMA zurück.

4. Die Einzelziffern der Gesamtsumme 112 geben das Kreisflächenverhältnis 1:3 der beiden konzentrischen Kreise wieder:

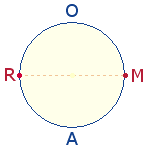
5. Die vier Buchstaben von ROMA lassen sich auf 2 Kreisachsenpunkte und 2 Kreisbogenhälften setzen:

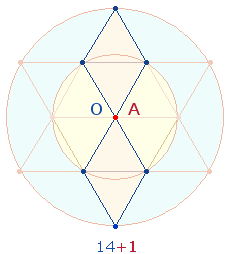
Es gehören nun RM und OA mit den ZW 17+12 und 14+1 zusammen. Aus 17+12 setzen sich die Rahmenelemente des DR-Kreuzes zusammen, aus 14+1 die Rahmenelemente einer einzelnen DR:

Um alle drei möglichen Silbenpaare zu erhalten, eignen sich die Querlinien des DR-Kreuzes:

Die drei Möglichkeiten sind demnach: RO-MA, RM-OA, RA-OM.

6. Nun kann man von dreimal zwei Buchstabenpaaren 6 Werte erstellen: von den ZS (1) und FS (2) deren FW (3,4) und von den addierten ZS+FS und FW-Summen wiederum die FW (5, 6):

	1	2		3	4			5	6
	ZS	FS	sm	FW	FW	sm	SM	FW	FW	SM	GS
RO	31	26	57	31	15	46	103	22	25	47	150
MA	13	8	21	13	6	19	40	10	19	29	69
	44	34	78	44	21	65	143	32	44	76	219
RM	29	24	53	29	9	38	91	53	21	74	165
OA	15	10	25	8	7	15	40	10	8	18	58
	44	34	78	37	16	53	131	63	29	92	223
RA	18	18	36	8	8	16	52	10	8	18	70
OM	26	16	42	15	8	23	65	12	23	35	100
	44	34	78	23	16	39	117	22	31	53	170
	132	102	234	104	53	157	391	117	104	221	612
234:378 = 18(13:21) = 1834; 391:221 = 17(23:13); 612 = 3617
117:104 = 13(9:8) = 1317; 70:100 = 10*(7:10)

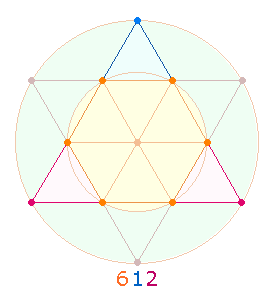
Die Ergebnisse sind erstaunlich: 17, der ZW der Initiale R von ROMA, ist – neben 13 – der bedeutendste Faktor. Die Einzelziffern der Gesamtsumme 612 geben 6 hexagonale Kreislinienpunkte und 1+2 Eckpunkte der Tetraktys wieder:

Der Durchschnitt der 18 Einzelwerte ist 34, die der 6 Buchstabenpaare 102 und der 12 Buchstaben 51. Die Gesamtsumme 170 des dritten Buchstabenpaares verbindet die addierten ersten beiden durch den Faktor 17.

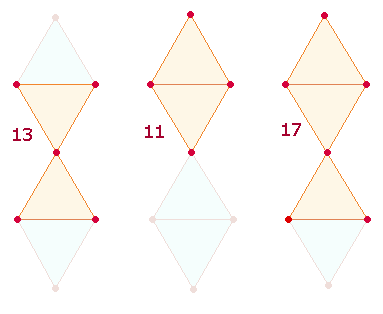
Durch die Erweiterung des Hexagons zum Tetraktysstern ergeben sich drei geometrische Figuren aus 13, 11 und 17 Elementen:

Die rechte "Fischfigur" hat trinitarische Bedeutung wegen ihrer drei Dreiecksflächen. Sie findet sich je dreimal in zwei Tetraktys und je zweimal in drei DR, die Summe der Elemente ist jeweils 102. Die anderen beiden Figuren sind darin eingebunden. Die FS des 3. Buchstabenpaares RA-OM verbinden die 17 Elemente der Fischfigur mit den 17 Elementen einer Oktaederhälfte:

	Pu.	Li.	F
Fisch	6	8	3
Okt.H.	5	8	4
	11	16	7
18+16 = 34

Die Linien haben Punkte zur Voraussetzung und ermöglichen die Bildung von Flächen. Daher gehören Punkte und Flächen zusammen. Dasselbe gilt für die 26 Elemente des Oktaeders: 6 Ecken + 8 Flächen werden durch 12 Linien verbunden. 14 und 12 sind die ZW von OM.

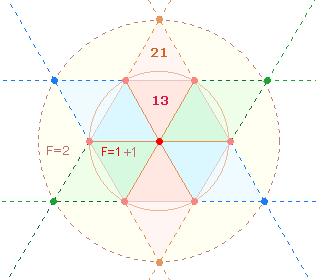
7. Das Verhältnis 70:100 = 10*(7:10) weist auf eine weitere herausragende Bedeutung der Zahl 17, zusammengesetzt aus 7 hexagonalen und 10 Tetraktyspunkten, die das Kreisflächenverhältnis 1:3 wiedergeben. Dasselbe Flächenverhältnis wird durch 13 Elemente des Doppeldreiecks und 21 Elemente der DR repräsentiert:

8. Die Zahl 17 ist auch Faktor der einzelnen und addierten Gesamtsummen:

	GS	FW	FW
RO	150		15
MA	69		26
	219	76	41	117
RM	165		19
OA	58		31
	223	223	50	273
RA	70		14
OM	100		14
	170	24	28	52
	612	323	119	1054
323:119 = 17*(19:7)
1054 = 31*34

Die drei addierten FW-Summen sind jeweils durch 13 teilbar, die erste und dritte bilden mit der zweiten das Verhältnis 169:273 = 13*(13:21).

Erstellt: August 2019

Inhalt 2