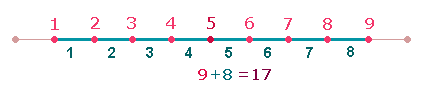Teil 1

HORAZ, CARMEN SAECULARE

Gematrische Gestaltung von 31 Götterbezeichnungen

TEIL 5:

6 Werte und die Zahl 29

I. Tabelle

II. Die Zahl 29

a) Komplimentärprinzip

b) Zwei weitere Bildungen der Zahl 29

c) Beispiele aus dem Carmen saeculare

III. Die 31 Bezeichnungen in Doppelrautenkreuz und Oktogon

I. Tabelle

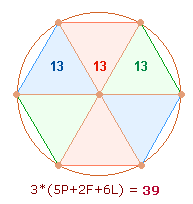
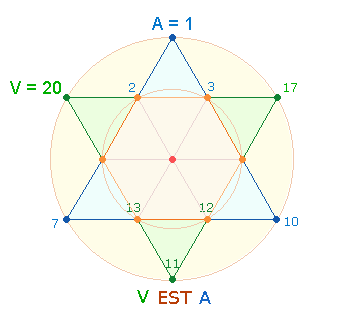
1. Die bisherige Untersuchung hat gezeigt, daß ZS, FS und Versnummern (VN) eine Einheit bilden. Nun berücksichtigen gematrische Konstruktionen außer den ZS und FS auch deren FW. Es stellt sich daher die Frage, ob Horaz so weit in seinem Ehrgeiz gegangen sei, daß er den drei ersten Werten noch deren FW zur Seite stellen wollte. Man könnte an die drei Doppeldreiecke des Hexagons denken, die einerseits in 3+3 durch die Mittelachse getrennt sind, von denen andererseits jedem Dreieck ein spiegelsymmetrisches gegenübersteht:

Tatsächlich spricht einiges für eine solche umfassende Konzeption des Dichters. Es folgt eine Tabelle mit den 3+3 Werten in paralleler Anordnung:

	ZS	FS	VN	sm	FW	FW	FW	sm	GS
PHOEBE	49	35	1	85	14	12	1	27	112
DIANA	28	25	1	54	11	10	1	22	76
DIS	31	18	7	56	31	8	7	46	102
SOL	43	28	9	80	43	11	6	60	140
ILITHYIA	88	68	14	170	17	21	9	47	217
LUCINA	57	43	15	115	22	43	8	73	188
GENITALIS	92	76	16	184	27	23	8	58	242
DIVA	34	20	17	71	19	9	17	45	116
PARCAE	42	35	25	102	12	12	10	34	136
TELLUS	84	63	29	176	14	13	29	56	232
CEREREM	64	59	30	153	12	59	10	81	234
IOVIS	70	38	32	140	14	21	10	45	185
APOLLO	66	49	34	149	16	14	19	49	198
LUNA	45	34	36	115	11	19	10	40	155
LARES	52	42	39	133	17	12	16	45	178
DI	13	10	45	68	13	7	11	31	99
DI	13	10	46	69	13	7	25	45	114
VENERISQUE	128	85	50	263	14	22	12	48	311
FIDES	42	28	57	127	12	11	22	45	172
PAX	37	19	57	113	37	19	22	78	191
HONOS	67	45	57	169	67	11	22	100	269
PUDORQUE	111	69	57	237	40	26	22	88	325
VIRTUS	103	68	58	229	103	21	31	155	384
COPIA	42	27	60	129	12	9	12	33	162
PHOEBUS	82	47	62	191	43	47	33	123	314
CAMENIS	61	43	62	166	61	43	33	137	303
DIANA	28	25	70	123	11	10	14	35	158
IOVEM	60	36	73	169	12	10	73	95	264
DEOSQUE	82	48	73	203	43	11	73	127	330
PHOEBI	53	36	75	164	53	10	13	76	240
DIANAE	33	30	75	138	14	10	13	37	175
TS1 4341	1800	1259	1282	4341	828	561	592	1981	6322
TS2 1981	828	561	592	4341 = 3*1447 >1450=50*29
sm	2628	1820	1874	1981 = 7*283 > 290 = 10*29
				6322 = 2*29*109 > 140
1450:290 = 290*(5:1)

Man muß sich vorstellen, daß Horaz mit den 6 Werten variabel umging. In einigen Zusammenhängen sind alle 6 relevant, in anderen 2, 3 oder 4. Dabei greifen die Relevanzen der verschiedenen Konstellationen ineinander.

Die im ersten Teil hervorgehobene Bedeutung von DIS findet mit den 6 Werten ihren Abschluß: Die Gesamtsumme 102 entspricht der ZS der 8 verschiedenen Buchstaben des SATOR-Quadrats PENSATOR – der im Gleichgewicht Haltende, der Vergeltende. Auch die Zusammensetzung von PEN und SATOR läßt sich gematrisch zusammenstellen:

	FS	FW	FW	sm		ZS	FW	VN	sm	GS
PEN	18	8	7	33	SATOR	31	31	7	69	102

2. Horaz verbindet beide Teilsummen (TS) nicht durch einen gemeinsamen Teiler, sondern durch den Faktor 29 ihres jeweiligen FW, der sich auch als Faktor der Gesamtsumme 6322 erweist. 2*109 bezieht sich auf zwei Tetraktys, bestehend aus 10 Punkten und 9 Dreiecken. Zu 218*29 kommen also noch 60*29 hinzu, zusammen 278*29 = 8062 = 2*139*29:

			sm	FW	sm	FW	sm
TS	4143	1981	6322	140
FW	1450	290	1740	41
sm	2*29*139		8062	181	8243	8243
FW			170	181	251	251
sm						8494
FW	8494 = 2*31*137					170

Auffälliges Ergebnis der ZW/FW-Verrechnung ist zweimal der FW 170 mit benachbarten Faktoren. Die Berechnung ist nach dem zweiten FW 170 nicht mehr fortführbar, da 8243 und 251 Primzahlen sind.

3. Die Aufteilung der Summe 2628 in 26+28 = entspricht den Konstitutivzahlen für ihre Summe 54. Das FS:ZS-Verhältnis 828:1800 beträgt 36*(23:50). Die Differenz der beiden Verhältniszahlen beträgt 27.

4. Die Primzahl 1259 wird erst durch ihre Addition mit 561 = 33*17 verstehbarer: 182 ist die ZS von SATOR OPERA TENET – Der Schöpfer erhält seine Werke. Mehr zur Bedeutung der Zahl 182.

II. Die Zahl 29

a) Komplimentärprinzip

1. Wenn Horaz der Zahl 29 eine so herausragende Bedeutung einräumt, kommt ihr offensichtlich höchste göttliche Seinswirklichkeit zu. Von den verschiedenen Aspekten dieser Zahl greife ich die auf, der hier am zutreffendsten erscheinen. Es handelt sich um einen verflochtenen Sachverhalt, dem die Darstellung nicht völlig ausweichen kann: Es sind eine Reihe von Einzelschritten und Einschüben erforderlich. Die Aufgabe, die offensichtlich zu bewältigen ist, besteht darin, zwei vergleichbare Flächenfiguren, denen einmal zwei und einmal drei Achsen zugrunde liegen, in Übereinstimmung zu bringen. Letztlich geht es um den Tetraktysstern und das 5*5-Punkte Quadrat, die Grundlage des SATOR-Quadrats (SQ). Nur von daher sind die Buchstaben V (20) und I (9), die als Zahlzeichen (5 u.1) eine entscheidende Funktion haben, zu erklären.

2. Ausgangspunkt der Zahl 29 sind die Grundzahlen 1-9, die, als Punkte aufgefaßt, 8 Maßeinheiten begrenzen:

Die Zahlen 9 und 8 sind in konzentrischer Sichtweise Komplimentärzahlen zu 1 und 2, die als Kardinalzahlen 1+2 die drei göttlichen Personen darstellen. Die Summe der zwei komplementären Paare ist 3+17 = 20.

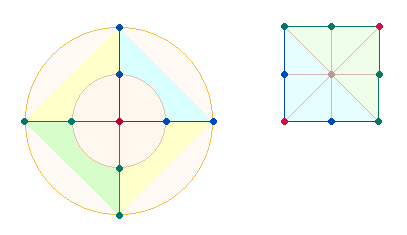
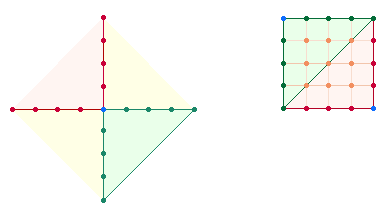
3. Die Zahlen 9 und 8 sind in einem Achsenkreuz von 9 Punkten (P) und 8 Maßeinheiten (ME) darstellbar:

Jeder der 4 Achsenarme besteht aus 5 Elementen, 3 P+2 ME. Bei einem Mittelpunkt entfallen drei Elemente, eben die der Komplementärzahlen 1+2. Beide Zählweisen 20+17 ergeben die 37 Elemente der Tetraktys.

Die Zahl 9 bezieht sich nicht nur auf die Zahl der Punkte, sondern auch auch auf die Elemente einer einzelnen Achse. Wenn man jedoch für jeden Achsenarm 5 Elemente zählt, ist zu 9 noch 1 hinzuzufügen. Dies wird durch den Buchstaben I geleistet, der den ZW 9 hat und als Zahlzeichen 1 bedeutet.

Die vier Achsenarme werden durch Winkelverschiebung zu 4 Seiten eines Quadrats. Durch Einziehen eines Achsenkreuzes erhält man 4 Einzelquadrate. Dieses Quadrat aus 2 ME je Seite besteht aus 25 Elementen: 9 Punkten + 4 Einzelquadraten und 12 Linien.

Durch die Winkelverschiebung reduziert sich die Zahl der Achsenelemente von 9 auf 5. Gesucht ist daher ein erweitertes Quadrat mit 9 Achsenelementen.

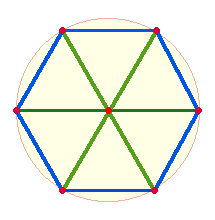
4. Beschreibt man um einen Kreislinienpunkt einer Kreisachse einen Kreis durch den Mittelpunkt, erhält man zwei Schnittpunkte als Ausgangspunkt zweier weiterer Achsen. Verbindet man die Kreislinienpunkte, erhält man 6 gleichseitige Dreiecke, 3 je Halbkreis:

Auch diese Figur des Hexagons besteht aus 25 Elementen: 7 Punkten + 6 Dreicken und 12 Linien. Gemeinsam sind beiden Flächenfiguren 5 Elemente der Mittelachse, die sich um ihr Quadrat vermehren.

Der Buchstabe V hat den ZW 20, als Zahlzeichen bedeutet er 5. Die Zahl 20 ist auf 4*5 Elemente der vier Quadratseiten beziehbar, die Grundeinheit 5 führt demnach durch Addition von 20 zur Vollzahl von 25 Elementen.

5. Das V hat Symbolcharakter: Als zweite Tetraktys fügt sie der ersten 10 weitere Punkte hinzu. A bildet den Anfang, V das Ende der Punktezahl:

Verlängert man die Segmentlinien des Hexagons, entsteht durch 6 Schnittpunkte ein Hexagramm, ein Sechseckstern oder Tetraktysstern. Nun hat man als Durchmesser eine charakteristische Zickzacklinie aus 9 Elementen und 2*5 Radialelemente, die auf den Buchstaben I zutreffen.

Um ein entsprechendes Quadrat zu bilden, braucht man ein Achsenkreuz als Grundlage, dessen einzelne Achse aus 9 Punkten und 8 Linien (=ME) besteht, sodaß das daraus entstehende Quadrat einen inneren und äußeren Quadratrahmen besitzt wie der Tetraktysstern einen inneren und äußeren Kreis. Dieses 5*5 Punkte Quadrat aus einem Achsenkreuz von 33 Elementen (17+16) ist Grundlage des SQ:

Der Buchstabe V bezieht sich nun ausschließlich auf 20+5 Punkte, der Buchstabe I , unter Einbeziehung der Linien, auf 9 Achsenelemente und gleichviele Elemente jeder Quadratseite. Wenn man nun die Zahl 4 einmal auf die 4 Quadratseiten und einmal auf die Linien einer einzelnen Quadratseite bezieht, läßt sich die entscheidende Formel für 29 bilden:

4*5 + 4+5 = 29

4+5 stellt gleichzeitig die Addition der Primzahlfaktoren der Zahl 20 dar, die genauer 2*2*5 sind. Also ist die Zahl 29 zunächst definiert als ZW 20 und FW 9.

Den 25 Punkten des Quadrats entsprechen im Tetraktysstern 13 Punkte und 12 Dreiecke.

6. Die ZW 9 und 20 für die Buchstaben I und V sind andererseits eigenständige Größen (9 also nicht abhängig von 20) wie auch ihre Erweiterung um 1 und 5 zu 10+25 = 35, die diese beiden Buchstaben als Zahlzeichen leisten. Es gilt, ihre jeweiligen FW miteinzubeziehen. Sie erfolgt in zwei Kombinationen:

I.	DmE	QR	sm	RE	QE	sm	GS
Zahl	9	20	29	10	25	35	64
FW	6	9	15	7	10	17	32
sm	15	29	44	17	35	52	96

II.	DmE	RE	sm	QR	QE	sm	GS
Zahl	9	10	19	20	25	45	64
FW	6	7	13	9	10	19	32
sm	15	17	32	29	35	64	96

Das FS:ZS-Verhältnis ist 32*(1:2).

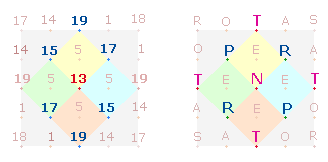
Die Ergebnisse der beiden Gruppierungen sehen nach einem relevanten Modell des SQ aus: Die vier verschiedenen FS 15, 17 und 19, 13 befinden sich auf den Punkten der vier kleinen Rautenquadrate:

Charakteristisch für die Werte des Rautenquadrats ist der Wechsel des Faktors 32 und 23: Die ZW der vier Eckpunkte ergeben 2*32 und schlagen um zur Umkehrform 3*23, wenn man die Mittelpunktszahl 5 hinzufügt. Die Summe des vertikalen Punktemusters 3+1+3 (li. Grafik) beträgt 51+13+51 = 115 = 5*23. In der Zahl 115 erkennt man die 2+5 Punkte der Doppelraute, in 5*23 die Radialelemente des Tetraktyssterns. Die Einzelziffern der Umkehrzahlen 23 und 32 als Summe der Zahlen 1-10, entsprechen dem Grundmuster von 2 und 3 Achsen, die in der Oktaederbildung zusammenwirken.

Als bedeutende Ergebnisse sind die ZS+FS 44 und 52 einzustufen. Sie stellen die Elemente von je 4 Rauten und 4 sanduhrförmigen Doppeldreiecken dar: Erstere sind erkennbar, wenn man den Oktaeder von der oberen zur unteren Spitze betrachtet, letztere, wenn man die obere und untere Ecke jeweils als Mittelpunkt eines Doppeldreiecks annimmt. Die Summe 96 = 3*32 = 4*24 ergibt sich im Rautenquadrat des SQ, wenn man 4*(19+5) = TE rechnet. Das Modell hierfür ist die schleifenförmige Punktenumerierung der Doppelraute, deren beide Spitzen sich bei der Oktaederbildung vereinigen:

7. Unter Aussparung der 4 E = 20 zeigt sich im SQ die Relevanz der Zahl 17. Die drei ZW 19+15+17 = 51 = 3*17 wiederholen in Produktform die komplementäre Addition 3+17. Modell sind drei "Fischfiguren" von je 17 Elementen je Tetraktys. Die Gesamtsumme des Rautenquadrats ohne 20 ist 153 = 9*17, die Summe der Zahlen 1-17, und 173 mit 20, was als Addition 17+3 verstanden werden kann.

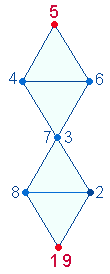
b) Zwei weitere Bildungen der Zahl 29

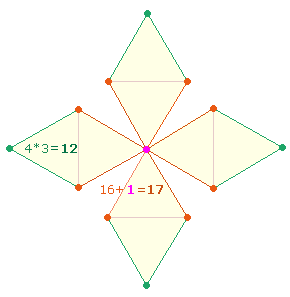
1. Der Rechnung 4*5 + 4+5 entsprechen die Zahlen 8+9 = 17 und deren FW 6+6 = 12. Als Modell eignet sich das DR-Kreuz, dessen 29 Rahmenelemente zusammensetzbar sind aus 17 Elementen des hexagonalen Anteils und 12 Elementen der Erweiterung:

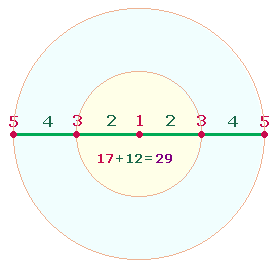
2. Wenn man eine Achse aus 9 Elementen vom Mittelpunkt aus von 1-5 numeriert, ist die Summe 29:

Die Aufteilung der Numerierung in ungerade und gerade Zahlen ergibt ebenfalls 17+12.

Bildet man aus einem so numerierten Achsenkreuz von Punkten ein Quadrat, kommen wie im SQ zweimal die Summe 1+14 = AO und zweimal 14+1 = OA zustande.

3. Noch nicht berücksichtigt wurden die Ausgangszahlen 1+2 = 3, deren FS ebensfalls 3 beträgt. Für diese Einzelzahlen 3+3 treten nun die Zahlzeichen VI sinnvoll und differenzierend ein. Sie bedeuten 5 Durchmesserelemente der Kreisachse, die durch einen weiteren Mittelpunkt in 2*3 Radialelemente geteilt werden.

Die Summe 29+6 = 35 teilt sich in die ZS 3+17 = 20 und die FS 3+12 = 15 auf. Das FS:ZS-Verhältnis ist demnach 5*(3:4).

Eine Affinität zur Tetraktys ergibt sich aus den dreistelligen Zusammensetzungen 29-6 = 8*37 und 6-29 = 17*37.

c) Beispiele aus dem Carmen saeculare

Zu den in Abschnitten a) und b) dargestellten Zusammenhängen der Zahlen 3+17, 29, 35, 23 und 32 sollen einige Beispiele angeführt werden:

1. Wie oben dargelegt, entsteht das 5*5-Punkte Quadrat aus einem Achsenkreuz von 33 Elementen: Die Summe der Zahlen 1-33 beträgt 33*17 = 561. Die Gesamt-ZS des Carmen Saeculare ist 20757 = 561*37.

2. Die ZS der 4 Eckpunkte des SQ-Rahmens beträgt 70, die der 4*2 jeweils angrenzenden Buchstaben A+O 60. Diesen ZS entsprechen die Namen IOVIS und IOVEM. Die ZS der 13 Buchstaben des Rautenquadrats ist 173 (s.o.). Dieselbe ZS haben die 5 Bezeichnungen DI DI DIS DIVA DEOSQUE:

IOVIS	70	38	32	140	14	21	10	45	185
IOVEM	60	36	73	169	12	10	73	95	264
DIS	31	18	7	56	31	8	7	46	103
DIVA	34	20	17	71	19	9	17	45	116
DEOSQUE	82	48	73	203	43	11	73	127	330
DI	13	10	45	68	13	7	11	31	99
DI	13	10	46	69	13	7	25	45	114
	303	180	293	776	145	73	216	434	1121
	483				218
651:560 = 7*(93:80) = 7*173

Horaz hat im Faktor 173 die Ausgangsaddition 17+3 beibehalten. Die 2+5 Bezeichnungen sind so in zwei Gruppen aufteilbar, daß sie durch 7 teilbar sind.

Die durchschnittliche Buchstabenzahl je Wort ist 4.

Eine Angleichung an das SQ zeigt auch die ZS+FS:

SQ	303	249	552
CS	303	180	483
	606	429	1035
552:483 = 69*(8:7)

69 = 3*23 ist die ZS von SATOR – Schöpfer. Da die ZS+FS von DI 23 beträgt, erhalten die übrigen 5 Wörter ihre Definition von diesem allgemeinen Begriff her. Das ZS+FS-Verhältnis von 3:2:2 Wörtern ist 23*(11:8:2): Man kann in den Verhältnisahlen 7 Punkte + 4 Dreiecke, 8 Linien und 2 Querlinien der DR erkennen. Gleiche ZS+FS 184 = 8*23 besteht zwischen zweimal OPERA und DIS DIVA.

Auch unter Einbeziehung der FW der ZS und FS hat DI den Durchschnittswert 43:

DI

13

10

13

7

43

	ZS	FS	FW	sm
SQ	303	249	252	804
CS	303	180	218	701
	606	429	470	1505
1505 = 35*43

Auch eine Mischung der beiden Wortgruppen ist möglich:

	ZS	FS	FW	sm		ZS	FS	FW	sm
SATOR	69	54	37	160	TENET	61	61	122	244
DEOSQUE	82	48	54	184	IOVIS	70	38	35	143
				344					387
344:387 = 43*(8:9)

3. Die Initialen von Wortgruppen, hier der 31 Bezeichnungen, werden in der Regel gematrisch berücksichtigt:

	A	C	D	F	G	H	I	L	P	S	T	V	sm
ZW	1	3	4	6	7	5	9	11	15	18	19	20	118
Hfk.	1	3	8	1	1	1	3	3	6	1	1	2	31
ZS	1	9	32	6	7	8	27	33	90	18	19	40	290
FS	1	9	32	5	7	6	18	33	48	8	19	18	204
494 = 2*13*19													494

Die FS 204 ist durch die Produktzahlen 12*17 mit der Zahl 29 verbunden. Die Palindromzahl 494 ist zu interpretieren als 49 Elemente des Tetraktyssterns, 2 Kreisbögen und 2 Kreisflächen. Sie ist die ZS der 6 Namen der Kapitolinischen Trias IUPPITER OPTIMUS MAXIMUS, IUNO REGINA, MINERVA.

4. Horaz könnte auch auf die Buchstaben IV besonders geachtet haben, deren Häufigkeit 22 und 14 beträgt und auf 2+2 Erweiterungselemente und 5 Durchmesserelemente des Hexagons beziehbar ist. Zwischen dem FW 9 und der Zahl 20 liegt die Differenz 11, zwischen 6 und 9 die Differenz 3. Da 22 durch 11 teilbar ist, ergibt sich ein Differenzverhältnis der beiden Buchstaben von 66:154 = 22*(3:7). Die ZS ist 198+280 = 478, die FS 478-220 = 258. Die ZW/FW-Verrechnung ergibt:

	ZS	FS	sm	FW	Fkt.
	478	258	736	33	23*32
FW	241	48	289	34	17²
sm				67

Das Quadrat von 17 sowie die Zahl 33 weist auf das oben besprochene Achsenkreuz aus 17 Elementen je Achse und 33 Elemente bei einem Mittelpunkt hin.

Erstellt: Juli 2011

Start

Inhalt