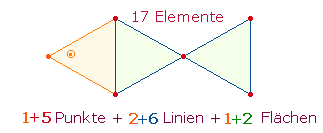
DÄDALUS UND
IKARUS
Die Zahlenwerte
I.
Überblick
II.
Zwei Texthälften
III.
Trinitarische
Komplementärzahlen
4Werte; Gleichheit von Vater und Sohn
I.
Überblick
1. Ovid hat für die 53 Zeilen ein gematrisches Ergebnis geplant und durchgeführt. Um es zu rekonstruieren, muß ein fehlerfreier Text gesichert sein. Das ist hier der Fall, da die ermittelten Faktoren auch in Teilbereichen zu finden sind. Ein Unsicherheitsfaktor betrifft Assimilationen von Präfixen. Wie die Dichter damit generell damit umgegangen sind, ist mir leider nicht bekannt. In diesem Text jedenfalls sind fünf Verben nicht assimiliert: CONPOSITAS (12) INPEDIEBAT (18) INPOSITAS (19) ADLIGAT (11) ADSPEXIT (51):
|
Daedalus interea Creten longumque perosus |
|
|
2 |
exilium tactusque loci
natalis amore |
|
3 |
clausus erat pelago. Terras licet, inquit, et undas |
|
4 |
obstruat, at caelum certe
patet; ibimus illac: |
|
5 |
Omnia possideat, non
possidet aera Minos. |
|
6 |
Dixit et ignotas animum dimittit in artes |
|
7 |
naturamque novat. nam ponit in ordine pennas |
|
8 |
a minima
coeptas, longam breviore sequenti, |
|
9 |
ut clivo
crevisse putes: sic rustica quondam |
|
10 |
fistula disparibus paulatim surgit
avenis. |
|
11 |
Tum lino
medias et ceris adligat imas |
|
12 |
atque ita conpositas
parvo curvamine flectit, |
|
13 |
ut veras imitetur aves. Puer Icarus una |
|
14 |
stabat et,
ignarus sua se tractare pericla, |
|
15 |
ore renidenti
modo, quas vaga moverat aura, |
|
16 |
captabat plumas,
flavam modo pollice ceram |
|
17 |
mollibat lusuque
suo mirabile patris |
|
18 |
inpediebat opus. Postquam manus ultima coepto |
|
19 |
inposita
est, geminas opifex libravit in alas |
|
20 |
ipse suum corpus motaque pependit in
aura. |
|
21 |
Instruit et natum medioque ut limite curras, |
|
22 |
Icare, ait moneo, ne, si demissior ibis, |
|
23 |
unda gravet pennas, si
celsior, ignis adurat: |
|
24 |
inter utrumque vola. nec
te spectare Booten |
|
25 |
aut Helicen iubeo
strictumque Orionis ensem: |
|
26 |
me duce carpe viam! pariter
praecepta volandi |
|
27 |
tradit et ignotas umeris accommodat
alas. |
|
28 |
Inter opus monitusque genae maduere seniles, |
|
29 |
et patriae tremuere manus;
dedit oscula nato |
|
30 |
non iterum repetenda suo pennisque levatus |
|
31 |
ante volat comitique timet, velut ales,
ab alto |
|
32 |
quae teneram
prolem produxit in aera nido, |
|
33 |
hortaturque sequi damnosasque erudit
artes |
|
34 |
et movet ipse suas et nati respicit
alas. |
|
35 |
hos
aliquis tremula dum captat harundine pisces, |
|
36 |
aut pastor baculo stivave innixus
arator |
|
37 |
vidit et obstipuit, quique aethera carpere
possent, |
|
38 |
credidit esse deos. Et iam Iunonia laeva |
|
39 |
parte Samos (fuerant Delosque Parosque
relictae) |
|
40 |
dextra Lebinthos erat fecundaque melle
Calymne, |
|
41 |
cum puer audaci coepit gaudere volatu |
|
42 |
deseruitque ducem caelique cupidine
tractus |
|
43 |
altius egit
iter. Rapidi vicinia solis |
|
44 |
mollit odoratas,
pennarum vincula, ceras; |
|
45 |
tabuerant cerae. Nudos quatit ille lacertos, |
|
46 |
remigioque carens non ullas percipit
auras, |
|
47 |
oraque caerulea
patrium clamantia nomen |
|
48 |
excipiuntur aqua, quae nomen traxit ab
illo. |
|
49 |
At pater infelix, nec iam pater, Icare, dixit, |
|
50 |
Icare, dixit, ubi es? Qua te
regione requiram? |
|
51 |
Icare, dicebat. Pennas adspexit in undis |
|
52 |
devovitque suas artes
corpusque sepulcro |
|
53 |
condidit, et tellus a nomine
dicta sepulti. |
Die Zahlensummen (ZS) der verschieden farbig markierten Zeileneinheiten sind durch 13 teilbar. Die Teilung durch 13 ergibt in der Reihe der 7 Zeileneinheiten folgende Faktoren: 157, 32, 157, 125, 833, 213, 147. 6 Texteinheiten von 27 Zeilen und der ZS 831*13 steht die zentrale Texteinheit von 26 Zeilen und die ZS 833*13 gegenüber. 833 und 831 sind die Konstitutivzahlen ihrer Summe 1664. Es folgen nun die Wortzahl, Buchstabenzahl und die ZS jeder einzelnen Zeile:
1.Daedalus (64) interea (69)
Creten (62) longumque (118) perosus (107)
5 (5) 37 (37) 420 (420)
2.exilium (87) tactusque (121)
loci (37) natalis (72) amore (49)
5 (10) 32 (69) 366 (786)
3.clausus (91) erat (42) pelago.
(53) Terras (77) licet, (47) inquit, (86) et (24) undas (56)
8 (18) 41 (110) 476 (1262)
4.obstruat, (110) at (20) caelum
(52) certe (49) patet; (59) ibimus (70) illac: (35)
7 (25) 37 (147) 395 (1657)
5.Omnia (49) possideat, (103)
non (40) possidet (102) aera (24) Minos. (66)
6 (31) 34 (181) 384 (2041)
6.Dixit (62) et (24) ignotas
(81) animum (67) dimittit (100) in (22) artes (60)
7 (38) 35 (216) 416
(2457)
7.naturamque (124) novat. (67) nam
(26) ponit (70) in (22) ordine (62) pennas (65)
7 (45) 37 (253) 436 (2893)
8.a (1) minima (56)
coeptas, (75) longam (58) breviore (89) sequenti, (105)
6 (51) 36 (289) 384 (3277)
9.ut (39) clivo (57)
crevisse (95) putes: (77) sic (30) rustica (87) quondam (80)
7 (58) 37 (326) 465 (3742)
10.fistula (84) disparibus (113) paulatim
(88) surgit (90) avenis. (66)
5 (63) 37 (363) 441 (4183)
11.Tum (51) lino (47) medias (49) et (24) ceris (52)
adligat (52) imas (40)
7 (70) 31 (394) 315 (4498)
12.atque (61) ita (29) conpositas (124)
parvo (67) curvamine (100) flectit, (72)
6 (76) 39 (433) 453 (4951)
13.ut (39) veras (61) imitetur (110) aves. (44) Puer
(57) Icarus (68) una (34)
7 (83) 32 (465) 413 (5364)
14.stabat (60) et, (24)
ignarus (85) sua (39) se (23) tractare (82) pericla, (61)
7 (90) 35 (500) 374 (5738)
15.ore (36) renidenti (94) modo, (44)
quas (55) vaga (29) moverat (88) aura, (39)
7 (97) 35 (535) 385 (6123)
16.captabat (61) plumas, (77)
flavam (51) modo (44) pollice (68) ceram (38)
6 (103) 36 (571) 339 (6462)
17.mollibat (79) lusuque (110) suo
(52) mirabile (66) patris (79)
5 (108) 32 (603) 386 (6848)
18.inpediebat (82) opus. (67)
Postquam (115) manus (64) ultima (72) coepto (70)
6 (114) 39 (642) 470 (7318)
19.inposita (98) est, (42)
geminas (65) opifex (70) libravit (88) in (22) alas (31)
7 (121) 38 (680) 416
(7734)
20.ipse (47) suum (70) corpus (87) motaque
(87) pependit (85) in (22) aura. (39)
7 (128) 35 (715) 437 (8171)
21.Instruit (124) et (24) natum (65)
medioque (85) ut (39) limite (65) curras, (76)
7 (135) 37 (752) 478 (8649)
22.Icare, (35) ait (29) moneo,
(58) ne, (18) si (27) demissior (106) ibis, (38)
7 (142) 30 (782) 311 (8960)
23.unda (38) gravet (69) pennas, (65)
si (27) celsior, (77) ignis (56) adurat: (62)
7 (149) 36 (818) 394 (9354)
24.inter (63) utrumque (129) vola. (46)
nec (21) te (24) spectare (83) Booten (67)
7 (156) 36 (854) 433 (9787)
25.aut (40) Helicen (54) iubeo (50)
strictumque (158) Orionis (94) ensem: (53)
6 (162) 38 (892) 449 (10236)
26.me (17) duce (32) carpe
(41) viam! (42) pariter (83) praecepta (81) volandi (72)
7 (169) 38 (930) 368 (10604)
27.tradit (69) et (24) ignotas (81)
umeris (81) accommodat (83) alas. (31)
6 (175) 35 (965) 369 (10973)
28.Inter (63) opus (67) monitusque (146)
genae (31) maduere (64) seniles, (79)
6 (181) 38 (1003) 450 (11423)
29.et (24) patriae (67) tremuere (100) manus; (64) dedit
(41) oscula (67) nato (47)
7 (188) 37 (1040) 410 (11833)
30.non (40) iterum (82)
repetenda (84) suo (52) pennisque (114) levatus (94)
6 (194) 37 (1077) 466 (12299)
31.ante (38) volat (65) comitique (107)
timet, (64) velut (75) ales, (35) ab (3) alto (45)
8 (202) 38 (1115) 432 (12731)
32.quae (42) teneram (72)
prolem (74) produxit (119) in (22) aera (24) nido, (40)
7 (209) 35 (1150) 393 (13124)
33.hortaturque (156) sequi (68) damnosasque (122)
erudit (74) artes (60)
5 (214) 38 (1188) 480 (13604)
34.et (24) movet (70) ipse (47) suas (57) et (24) nati
(42) respicit (95) alas. (31)
8 (222) 33 (1221) 390
(13994)
35.hos (40) aliquis (84) tremula (85) dum
(36) captat (58) harundine (90) pisces, (68)
7 (229) 41 (1262) 461 (14455)
36.aut (40) pastor (84)
baculo (51) stivave (92) innixus (103) arator (69)
6 (235) 35 (1297) 439 (14894)
37.vidit (61) et (24) obstipuit, (125)
quique (86) aethera (56) carpere (63) possent, (102)
7 (242) 43 (1340) 517 (15411)
38.credidit (70) esse (46) deos. (41) Et
(24) iam (22) Iunonia (79) laeva (38)
7 (249) 33 (1373) 320 (15731)
39.parte (57) Samos (63) (fuerant (81)
Delosque (93) Parosque (106) relictae) (70)
6 (255) 41 (1414) 470 (16201)
40.dextra (67) Lebinthos (99) erat (42)
fecundaque (93) melle (44) Calymne, (67)
6 (261) 41 (1455) 412 (16613)
41.cum (35) puer (57) audaci (38) coepit (65) gaudere
(59) volatu (85)
6 (267) 32 (1487) 339 (16952)
42.deseruitque (138) ducem (44) caelique (70)
cupidine (78) tractus (97)
5 (272) 39 (1526) 427 (17379)
43.altius (78) egit (40) iter. (50)
Rapidi (55) vicinia (64) solis (70)
6 (278) 32 (1558) 357 (17736)
44.mollit (76) odoratas, (88) pennarum (96)
vincula, (77) ceras; (44)
5 (283) 34 (1592) 381 (18117)
45.tabuerant (97) cerae. (31) Nudos (69)
quatit (84) ille (36) lacertos, (88)
6 (289) 37 (1629) 405 (18522)
46.remigioque (114) carens (57) non (40)
ullas (61) percipit (92) auras, (57)
6 (295) 37 (1666) 421 (18943)
47.oraque (73) caerulea (63)
patrium (93) clamantia (70) nomen (57)
5 (300) 35 (1701) 356 (19299)
48.excipiuntur (151) aqua, (38)
quae (42) nomen (57) traxit (86) ab (3) illo. (45)
7 (307) 36 (1737) 422 (19721)
49.At (20) pater (57)
infelix, (74) nec (21) iam (22) pater, (57) Icare, (35) dixit, (62)
8 (315) 35 (1772) 348 (20069)
50.Icare, (35) dixit, (62) ubi
(31) es? (23) Qua (37) te (24) regione (70) requiram? (97)
8 (323) 35 (1807) 379 (20448)
51.Icare, (35) dicebat. (43)
Pennas (65) adspexit (92) in (22) undis (64)
6 (329) 33 (1840) 321 (20769)
52.devovitque (132) suas (57) artes (60)
corpusque (128) sepulcro (103)
5 (334) 36 (1876) 480 (21249)
53.condidit, (75) et (24) tellus (84) a (1)
nomine (66) dicta (36) sepulti. (97)
7 (341) 35 (1911) 383 (21632)
a(216) e(228) i(192) o(103) u(173) V
912 7986
b(21) c(74) d(59)
f(7) g(17)
h(6) l(76)
m(78) n(110)
p(67) q(38)
r(122) s(135)
t(176) x(12)
y(1) 16 k,z
K 999 13646
Die gelb und grün markierten Summen sind
jeweils durch 13 teilbar.
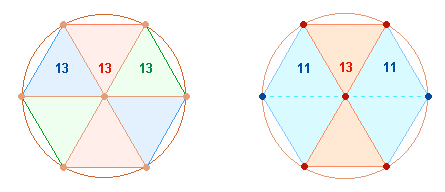
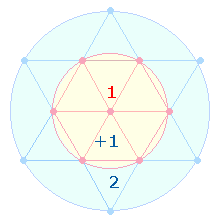
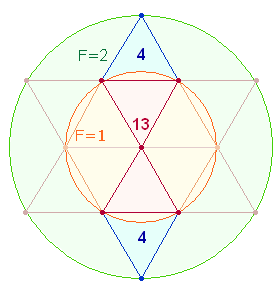
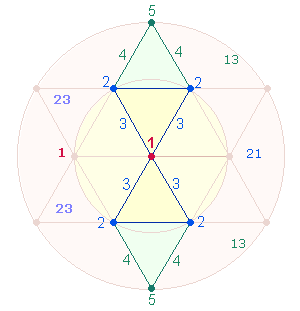
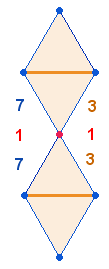
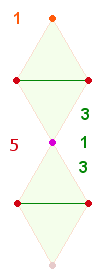
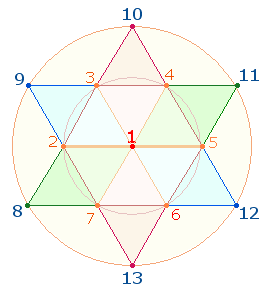
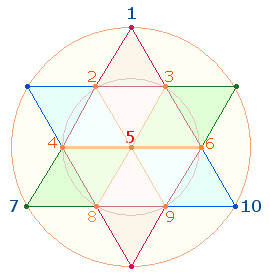
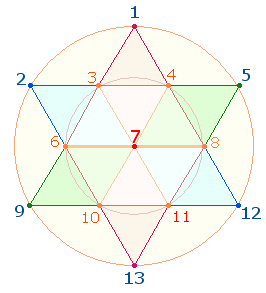
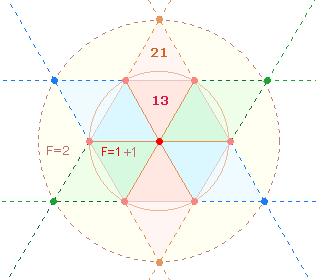
2. Es ist schon zu Beginn festzuhalten, daß Ovids außerordentliche gematrischen Bemühungen höchsten religiösen Aussagen gelten und daß zahlreiche Konstruktionen in Bezug zu diesen Bemühungen zu sehen sind. Aus dem Tetraktysstern ist die Wirklichkeit einer Gemeinschaft und Einheit dreier göttlicher Personen erkennbar. Dies ist in der Folge in immer wieder neuen Variationen aufzuzeigen. Daedalus und Icarus werden von Ovid als Archetypus der ersten und abbildhaft gleichen zweiten Person verstanden, wie die folgende Figurenkonstellation im Hexagon nahelegt:
|
|
Das rechte Hexagon zeigt zwei Rauten von je 11 Elementen, die durch ein mittleres Doppeldreieck aus 13 Elementen miteinander verbunden sind.
3. Der Faktorenwert (FW) der ZS 21632 ist 128*169 = 27*13² = 14+26 = 40. Die Faktoren umfassen bereits die wesentlichen trinitarischen Verhältnisse im Tetraktysstern. Dabei vertreten sich geometrische Elemente nicht selten gegenseitig:
·
Die Einzelziffern der Zahl 128 sind auf den Doppelaspekt
von 5
Durchmesser- und 3+3 Radialelemente der
Kreisachse mit 1 und 2 Mittelpunkten beziehbar. Für die vorliegende Geschichte
bedeutender jedoch erscheinen die 11
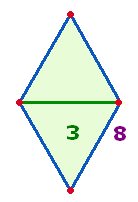
Elemente der Raute, die ja einen Flügel in stilisierter Weise darstellt. Die
Raute besteht demnach aus 3 Binnenelementen
und 8 Rahmenelementen: Die Rautenfläche wird
durch 1 Linie in 2
Hälften geteilt, die Rahmenelemente bestehen aus 4+4 Punkten + Linien:
|
|
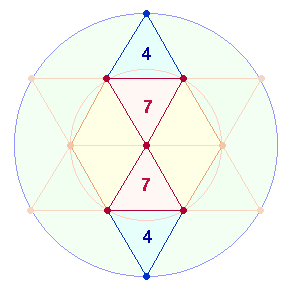
27 = FW 14 kann auf 2+7 Elemente zweier Kreishälften sowie auf zweimal 7 Punkte des Tetraktyssterns verweisen, wenn um die 13 Punkte des Tetraktyssterns ein Kreisbogen geschlagen wird, so daß der hexagonale Mittelpunkt ein zweites Mal benutzt wird. Denn nur so kommt das Kreisflächenverhältnis 1:3 zustande, das sich als wesentliches Modell der Einheit in der Dreiheit offenbart. 2+7 kann auch auf 2 Querlinien + 7 Punkte, der FW 14 auf 10 Linien + 4 Flächen der DR verweisen.
·
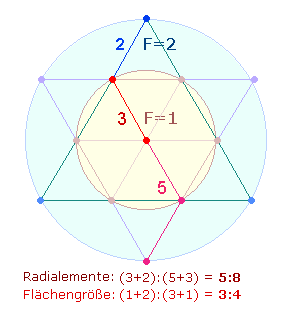
Setzt
man die Radialelemente der DR in Bezug zu
den Kreisflächeneinheiten 1+2 und 1+3, ergibt sich durch 3+2 und 3+5 die
Summe 5+8 = 13:
|
|
Da sich die Radialelemente vom Mittelpunkt zweimal zählen lassen, ergibt sich aus der oben ermittelten FS 14+26 zweimal das Verhältnis von 7 Kreisflächeneinheiten zu 13 Radialelementen.
Die FS 40 selbst repräsentiert durch das Produkt 5*8 ebenfalls 7 Flächeneinheiten.
·
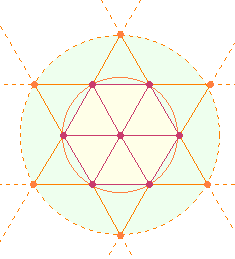
Das Kreisflächenverhältnis 1:3 ist auch darstellbar durch 7 hexagonale Punkte zu 13
Punkten des Tetraktyssterns, wobei der Mittelpunkt nur einmal gezählt wird.
Zweimal 7:13 Punkte entsprechen dem Paar von
Vater und Sohn.
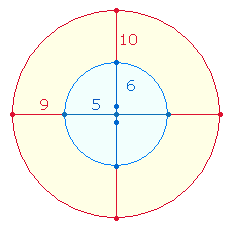
4. Die Zahl 13 ist auch Faktor der Buchstabenzahl 1911 = 7*7*(3*13) >FW 14+16 = 30, der Umkehrfaktor 31 ist in der Wortzahl 341 = 11*31 >FW 42 enthalten. Die Zahlen 19 und 11 setzen sich aus den Durchmesserelementen und Radialelementen der beiden konzentrischen Tetraktyskreise und des Hexagons zusammen, hier veranschaulicht an den Durchmesserlinien zweier konzentrischer Kreise:
|
|
Die Zahl 1911 ist bemerkenswert, da sowohl 19+11 als auch die FW 14+16 dieselbe Summe 30 ergeben. Dabei setzt sich 14 aus 5+9 Durchmesserelementen und 16 aus 6+10 Radialelementen zusammen. Dem Verhältnis 5:9 und 6:10 = 2*(3:5) entsprechen jeweils das Kreisflächenverhältnis 1:3. Die FW der ZS 21632, der Buchstabenzahl 1911 und der Wortzahl 341 sind (40+30)+42 = 112, das Verhältnis 70:42 = 14*(5:3) weist wiederum auf 2*7 Punkte des Tetraktyssterns und 5:3 Radialelemente hin, die Einzelziffern von 112 auf 1+(1+2) Kreisflächeneinheiten:
|
|
1. Von zwei Texthälften kann man sprechen, da bei fortlaufender Zählung erst nach 26 Zeilen von Z.16 bis Z.41 die durch 13 teilbare ZS 833*13 zustande kommt, 26 aber die untere Konstitutivzahl der Gesamtzahl von 53 Zeilen ist. Die ZS der oberen Konstitutivzahl 27 ist 831*13. Nun sind 833 und 831 selbst Konstitutivzahlen, so daß, wenn sich die größere mit der kleineren Zeilenzahl 26 verbindet und umgekehrt, sich wiederum die angrenzenden Zahlen 858+859 = 1717 ergeben. Die FW der beiden Zahlen sind 2*3*11*13 = 29 und 859, zusammen 888. Die Ergebnisse erlauben mehrere Interpretationen:
·
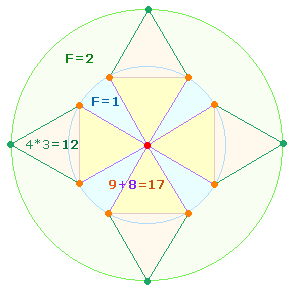
Die Einzelziffern 8+5 =
13 sind auf 6 Linien + 2 Flächen und 5
Punkte des sanduhrförmigen Doppeldreiecks als hexagonalen Bereich der DR beziehbar:
|
|
Zum Erweiterungsbereich
gehören 2*4 = 8 Elemente. 13:8 DR-Elemente geben das Kreisflächenverhältnis 1:2 wieder, 13:9
Elemente das Flächenverhältnis 1:3, indem ein
weiterer Mittelpunkt hinzukommt.
Aus 13+8 und 13+9
Elementen läßt sich ein DR-Kreuz mit 1+2 Mittelpunkten bilden. Das DR-Kreuz besteht also aus 21+22
= 43 Elementen.
Die Einzelziffern der FS 888 weisen
auf die Oktaederbildung hin. Denn durch die Vereinigung der äußeren Punkte der DR verkürzt sich die Zahl der Elemente der zwei Zickzacklinien und der Mittelelemente von 9
auf 8.
·
Die ZS 1717 ist auf die Elemente von zwei Oktaederhälften
beziehbar, die aus je 8 Elementen der
Mittelbasis und 9 Elementen des
Pyramidenaufsatzes bestehen.
Die ZS+FS 1717+888 = 2605 = 5*521 >FW 526 führt zweimal auf die 13 Elemente des hexagonalen Doppeldreiecks zurück, das jeweils mit denselben Ziffern aus 5 Punkten, 2 Flächen und 6 Linien besteht.
·
Die FW der
Ausgangszahlen 833 und 831
sind 7*7*17 > 31
und 3*277 > 80,
zusammen 311. Die FS 311
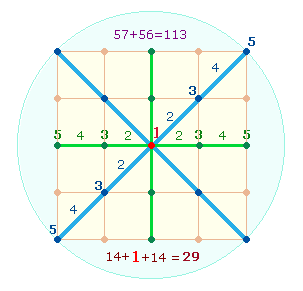
ist die Umkehrzahl des Grundmodells 113, das
die Kreisachse aus 2 Radialmaßen und 3 Begrenzungspunkten widerspiegelt. Die ZW/FW-Verrechnung
ergibt:
|
|
|
|
sm |
FW |
sm |
FW |
|
ZS |
833 |
831 |
1664 |
27 |
|
|
|
FW |
31 |
280 |
311 |
311 |
|
|
|
sm |
|
|
1975 |
338 |
2313 |
263 |
|
FW |
|
|
89 |
28 |
117 |
19 |
|
sm |
|
|
|
|
|
282 |
|
1975 = 25*79; 338 = 2*13² >28;
282 = 6*47 >52 |
||||||
|
2313 = 9*257 >263 |
||||||
Die Faktoren 7*7*17 von 833 sind auf 49 Elemente oder 7+7 Punkte des Tetraktyssterns und auf 7+10 Punkte des Hexagons und der Tetraktys beziehbar. Die Umkehrzahl 338 jedoch weist auf die Elemente des DR-Rahmens mit dem Ziel der Oktaederbildung. Denn da beim Zusammenfall der äußeren Punkte von 7 Punkten einer wegfällt, bleibt das Muster 3+3 Punkte + 8 Linien übrig:
|
|
Die Faktoren 2*13*13, zu lesen als 2*(13+13) = 52, stellen 4 Doppeldreiecke aus je 13 Elementen dar, aus denen die Oberfläche des Oktaeders besteht. Die Einzelziffern des FW 282 weisen auf 4 Flächen und 8 Rahmenlinien der DR hin.
·
Auch die ZW/FW-Verrechnung der 27 und 26
Zeilen sind von Bedeutung:
|
|
|
|
sm |
FW |
sm |
FW |
|
ZS |
27 |
26 |
53 |
53 |
|
|
|
FW |
9 |
15 |
24 |
9 |
|
|
|
sm |
|
|
77 |
62 |
139 |
139 |
|
FW |
|
|
18 |
33 |
51 |
20 |
|
sm |
|
|
|
|
|
159 |
|
159 = 3*53 |
||||||
Die Berechnung führt zum Dreifachen der Ausgangssumme 53. Die Einzelziffern weisen auf 2*3 Radialelemente und 5 Durchmesserelemente der Kreisachse hin.
·
Schließlich kann man die drei Zahlenpaare
zusammen verrechnen:
|
|
|
|
|
|
|
|
sm |
FW |
sm |
FW |
|
ZS |
27 |
26 |
833 |
831 |
859 |
858 |
3434 |
120 |
|
|
|
FW |
9 |
15 |
31 |
280 |
859 |
29 |
1223 |
1223 |
|
|
|
sm |
1343 = 17*79 |
4657 |
1343 |
6000 |
26 |
|||||
|
FW |
4753 = 7*7*97 |
4657 |
96 |
4753 |
111 |
|||||
|
sm |
|
137 |
||||||||
Setzt man den äußeren Kreisbogen voraus, entsprechen 13:7 Punkten des Tetraktyssterns und des Hexagons das Kreisflächenverhältnis 3:1.
Aus 15 Elementen besteht der DR-Rahmen, aus 9 Elementen die 6 Binnenelemente und 3 Vertikalpunkte. Aus den 11 und 13 Elementen der Raute und des Doppeldreiecks läßt sich der Oktaeder zusammensetzen.
2. Wie die obige Tabelle zeigt, sind die Zahlen 79 und 97 von großer konzeptioneller Wichtigkeit. Die Zahlen 9 und 7 sind Komplementärzahlen zu den trinitarischen Zahlen 1 und 3. Die Zahl 97 fiel auf als ZS 3*97 = 291 der 7 Wörter, die auf die 7 gegliederten Punkte der DR ausgerichtet sind. Ovids gematrische Grundvorstellung ist, Tetraktys und Doppelraute miteinander zu verbinden: Eine Zickzacklinie der DR – und die Mittelelemente – bestehen aus 9 Elementen, eine Tetraktysseite aus 7 Elementen.
Zum Dezimalsystem gehören untrennbar Doppelaspekte von Zählungen. Die Gesamtzahl von 53 Zeilen des Ovidtextes besteht aus dem Doppelaspekt von 26 Außenelementen und 26 Außenelementen + 1 Volumen. Ein weiterer Doppelaspekt zeigt sich in der Punktezählung der drei Hexagonachsen: Jede Achse besteht aus 3 Punkten, zusammen 9 Punkten. Rechnet man den Mittelpunkt nur einmal, sind es 7 Punkte.
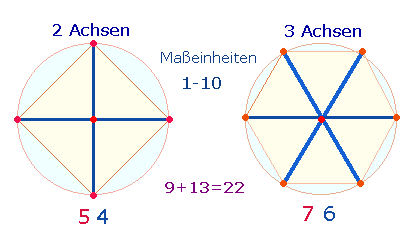
Nun werden für das Dezimalsystem 10 erforderliche Maßeinheiten durch ein zweiachsiges und dreiachsiges Achsenkreuz dargestellt:
|
|
10 Maßeinheiten werden durch 12 Punkte begrenzt. Wiederholt man dasselbe mit einem Mittelpunkt je Achse, lautet das Verhältnis 10:15, zusammen 20:27 oder 22:25. Rechnet man nur die Punkte, ergibt der Doppelaspekt 12+15. Dies sind jedoch die Zeilenzahlen, die die 26 durch 13 teilbare Zeilen-ZS eingrenzen.
Zwei und drei Achsen setzen eine einzige Achse voraus. Fügt man diese noch hinzu, beträgt das Verhältnis von Punkten zu Maßeinheiten 15:12. 15 und 12 Zeilen des Textes können also einen zweifachen Bezug haben:
|
|
2+3
Achsen |
|
1+2+3
Achsen |
|
GS |
||
|
ME |
10 |
10 |
20 |
12 |
12 |
24 |
44 |
|
Pu. |
12 |
15 |
27 |
15 |
18 |
33 |
60 |
|
|
22 |
25 |
47 |
27 |
30 |
57 |
104 |
|
44:60 = 4*(11:15); 104 = 8*13 |
|||||||
Im SATOR-Quadrat beträgt die Differenz zwischen den FS 54 und 40 zu den ZS 69 und 52 der Wörter SATOR und OPERA 15 und 12, und die FS der Wörter SATOR OPERA TENET ist 104:
|
|
ZS |
FW |
|
SATOR |
69 |
26 |
|
OPERA |
52 |
17 |
|
TENET |
61 |
61 |
|
|
182 |
104 |
|
104:182 = 26*(4:7) |
||
Einen Hinweis darauf, daß 15 Punkte und 12 Maßeinheiten gemeint sind, gibt die 4W-Summe 1692 der 14 mit A beginnenden Wörter: das Produkt 36*47 ergibt den FW 57.
Die reale Zahl 97 kommt zustande, wenn der Mittelpunkt des Tetraktyssterns mit 1, die übrigen 12 Punkte mit 2 und die 24 Linien mit 3 numeriert werden: 1+24+72 = 97. Die 12 Flächen, mit 4 numeriert, ergeben die Summe 48, die in der Aufteilung 2*(11+13) der Zusammensetzung des Oktaeders zugeordnet werden kann. Ovid bezieht mit den numerierten Flächen die DR mit ein.
Wie das Hexagon zum Tetraktysstern erweitert werden kann, so das rechtwinklige Achsenkreuz zum Quadrat mit 4 Achsen, die zu den 5+6 Achsen noch hinzukommen:
|
|
2+3
Achsen |
sm |
1+2+3
Achsen |
sm |
4 Achsen |
sm |
SM |
SM |
GS |
|||
|
ME |
10 |
10 |
20 |
12 |
12 |
24 |
12 |
12 |
24 |
34 |
34 |
68 |
|
Pu. |
12 |
15 |
27 |
15 |
18 |
33 |
17 |
20 |
37 |
44 |
53 |
97 |
|
|
22 |
25 |
47 |
27 |
30 |
57 |
29 |
32 |
61 |
78 |
87 |
165 |
Die Summe der Punkte ergibt wiederum die reale Zahl 97. Die Einzelziffern der Umkehrzahlen 78 und 87 lassen sich auf die Rahmenelemente eines DR-Kreuzes beziehen, sie sind die FS der 9 Primzahlen und 12 übrigen Zahlen von 1-21, ebenso der 12 konzentrischen Zahlen von 1-6, 21-16 und der übrigen 9 Zahlen.
Die numerierten Punkte und Linien des Tetraktyssterns können als komplementär gesehen werden:
|
|
|
Die Numerierungssummen sind:
|
|
numeriert |
|
unnum. |
|
||
|
|
TSt |
Qu |
sm |
TSt |
Qu |
sm |
|
Pu. |
25 |
65 |
90 |
13 |
13 |
26 |
|
Li. |
72 |
48 |
120 |
24 |
12 |
36 |
|
sm |
97 |
113 |
210 |
37 |
25 |
62 |
|
90:120 = 30*(3:4); 26:36 = 2*(13:18) |
||||||
Die Buchstabenzahl der 13 mit A beginnenden Wörter ist 62.
3. Die 6 durch 13 teilbaren Teilsummen der ZS 831 und der FW der ZS 833 sind:
|
Zeilen |
5 |
1 |
5 |
4 |
26 |
7 |
5 |
53 |
|
Zahl |
157 |
32 |
157 |
125 |
833 |
213 |
147 |
1664 |
|
FW |
157 |
10 |
157 |
15 |
31 |
74 |
17 |
461 |
|
+13 |
170 |
23 |
170 |
28 |
44 |
87 |
30 |
552 |
|
552
= 23*24 >FW 32 |
||||||||
Die FS der Primzahl 461 weist auf die Numerierung der Punkte und Linien hin:
|
|
Der Aufteilung 46+1 entspricht auch die Summe 23+24 = 47. Die Numerierung der 15 Rahmenelemente von 1-5 ergibt ebenfalls 47:
|
|
Die Einzelziffern der beiden angrenzenden Produktzahlen geben die 5 Durchmesser- und 6 Radialelemente der Kreisachse wieder. Zwei DR können einmal bis 23 und einmal bis 24 numeriert werden:yyy
|
|
Die besondere Bedeutung der Zahl 552 liegt darin, daß sie die ZS+FS 303+249 des SATOR-Quadrats ist.
Der FW 40 der Gesamt-ZS 21632 und der FW 32 der FS 552 haben außerordentliche trinitarische Bedeutung. Die beiden Kreisflächenverhältnissen 1:2 und 1:3 lassen sich auf ihre komplementäre Entsprechungen 9+8 und 9+7 übertragen und mit deren FW versehen. Das ergibt folgende beiden Tabellen:
|
|
|
|
sm |
|
|
sm |
GS |
|
ZW |
9 |
8 |
17 |
9 |
7 |
16 |
33 |
|
FW |
6 |
6 |
12 |
6 |
7 |
13 |
25 |
|
sm |
15 |
14 |
29 |
15 |
14 |
29 |
58 |
|
|
|
|
sm |
|
|
sm |
GS |
|
ZW |
3 |
17 |
20 |
4 |
16 |
30 |
40 |
|
FW |
3 |
12 |
15 |
4 |
13 |
17 |
32 |
|
sm |
6 |
29 |
35 |
8 |
29 |
37 |
72 |
Zusammen mit den Zahlen von 1-3 ergibt sich die ZS 40 und die FS 32. Die zweimalige ZS+FS 29 läßt sich durch zwei DR-Kreuze mit Aufteilung in ZS und FS darstellen:
|
|
|
Die beiden genannten Kreisflächenverhältnisse werden durch die Radialelemente 5:8 wiedergegeben.
4.
Die Teilsummen enthalten einige Besonderheiten:
|
Zahl |
157 |
32 |
157 |
125 |
471 |
833 |
213 |
147 |
1664 |
|
FW |
157 |
10 |
157 |
15 |
339 |
31 |
74 |
17 |
461 |
|
+13 |
170 |
23 |
170 |
28 |
391 |
44 |
87 |
30 |
552 |
|
471
= 3*157; 339:471 = 3*(113:157) = 3*270 |
|||||||||
Das Verhältnis von 4:3 FS beträgt 391:161 = 23*(17:7) und von 3:4 FS – bei Verschiebung des FW 23 – 368:184 = 184:(2:1).
Zwei Verseinheiten von je 5 Zeilen haben die ZS 157*13.
Die dritte ZS 157 , ebenfalls 5 Zeilen umfassen, ist aufgeteilt in 1+4 Zeilen und (32+125)*13. Ihre FS 25 hat zur ZS 157 die Differenz 132 hat, die ZS von DAEDALUS und ICARUS.
Welcher Zusammenhang besteht zwischen den beiden Zahlen 113 und 157, deren Differenz 44 = 4*11 die Zusammensetzung des Oktaeders durch 4 Rauten ermöglicht?
Zuerst ist die schwierige Primzahl 157 zu untersuchen. Denn in ihrer Verdoppelung 314 gibt sie die Gleichung 3+1=4 der DR-Punkte (mit 2 Mittelpunkten) wieder. Auf die DR bezogen läßt sich 157 in 15+7 aufteilen und 15 Rahmenelementen und 7 Binnenelementen zuordnen, sodaß 2*11 Elemente je einen Mittelpunkt haben:
|
|
Die Punktestruktur 313 ist damit auch für die Binnenelemente hergestellt.
Die Teilzahl 15 kann auch als 1+5 verstanden werden, wenn sich zur Oktaederbildung die beiden äußeren Punkte vereinigen:
|
|
Die Zahl 157 erscheint so als
Vorverweis darauf, daß erst mit dem Zustandekommen eines DR-Kreuzes die doppelte Zahl 314 zu ihrem Recht kommt.
Daß man 157 sinnvoll in 15+7 aufteilen kann, zeigt die Umkehrung 715 = 5*11*13 >FW 29. Die beiden ineinander geschobenen Figuren von Raute und sanduhrförmigem Doppeldreieck werden ja durch 113 in kontrahierter Form treffend dargestellt:
|
|
Die Bedeutung einer Zahl läßt sich aus ihren zwei Konstitutivzahlen untersuchen. Für 157 sind dies 79+78:
|
|
|
|
sm |
FW |
|
ZS |
79 |
78 |
157 |
157 |
|
FW |
79 |
18 |
97 |
97 |
|
sm |
|
|
|
254 |
|
254 = 2*127 |
||||
|
78 = 3*26 = 6*13 |
||||
Die ZW/FW-Verrechnung
hat wegen zweier Primzahl keine Fortsetzung und hat
daher gewissermaßen Absolutheitsrang. Die FS 254 gibt die 11
Elemente der Raute wieder: 2 Flächen, 5 Linien, 4
Punkte. Die Einzelziffern der Primzahl 127
verweisen auf 1+2+7 Punkte der Tetraktys, aber auch
auf die DR durch (7+5)+7
Punkte in der Bedeutung von (3+1)+3 Kreisflächeneinheiten. Die Umkehrzahl 452 = 4*113 enthält
bereits den Faktor 113, der das Ineinander von Raute
und sanduhrförmigem Doppeldreieck veranschaulicht.
Auch die 6
Umkehrzahlen von 157 können durch ihre FW Auskunft geben:
|
Zahl |
157 |
175 |
517 |
571 |
715 |
751 |
2886 |
|
FW |
157 |
17 |
58 |
571 |
29 |
751 |
1583 |
Die FS 1583 vereinigt die Raute mit dem Doppeldreieck zur "Fischfigur":
|
|
Die Faktoren der Konstitutivzahlen 792 = 72*11 >23 und 791 = 7*113 >120 ergeben 143 = 11*13. Tatsächlich ist 791 die FS der 6 Umkehrzahlen von 134:
|
Zahl |
134 |
143 |
314 |
341 |
413 |
431 |
1776 |
|
FW |
69 |
24 |
159 |
42 |
66 |
431 |
791 |
5. Die beiden Tetraktys im Hexagramm beherrschen zunächst das Bickfeld, die DR liegt eher verborgen. Deshalb scheint es Zeichen zu geben, die auf die DR hinführen sollen. Unter diesem Gesichtspunkt kann man die Zahl 157 als Zusammensetzung aus drei Ziffern betrachten, die bei unterschiedlichen Punktenumerierungen den Mittelpunkt besetzen. Die Numerierung des Tetraktyssterns kann vom Mittelpunkt 1 ausgehen und wie bei der Tetraktys vom oberen bis zum unteren Ende durchlaufen. Die Mitte der Tetraktys und des Sterns ist der 5. und 7. Punkt:
|
|
|
|
Die drei verschiedenen Numerierungen lassen sich auf verschiedene Figuren, besonders auf die 3*3 Doppelrauten anwenden. Dabei sind die hexagonalen Kreislinienpunkte doppelt und die Mittelpunkte dreimal zu zählen und auch die FW zu berücksichtigen:
|
|
6 au. |
6 hx |
MP |
sm |
6 au. |
6 hx |
MP |
sm |
FW |
|
Fig.1 |
63 |
27 |
1 |
91 |
63 |
54 |
3 |
120 |
14 |
|
Fig.2 |
18 |
32 |
5 |
55 |
18 |
64 |
15 |
97 |
97 |
|
Fig.3 |
42 |
42 |
7 |
91 |
42 |
84 |
21 |
147 |
17 |
|
|
123 |
101 |
13 |
237 |
123 |
202 |
39 |
364 |
128 |
|
364 = 2*13*14 |
|||||||||
|
|
6 au. |
6 hx |
MP |
|
6 au. |
6 hx |
MP |
|
FW |
|
Fig.1 |
50 |
26 |
1 |
77 |
50 |
52 |
3 |
105 |
15 |
|
Fig.2 |
15 |
26 |
5 |
46 |
15 |
52 |
15 |
82 |
43 |
|
Fig.3 |
34 |
36 |
7 |
77 |
34 |
72 |
21 |
127 |
127 |
|
sm |
99 |
88 |
13 |
200 |
99 |
176 |
39 |
314 |
185 |
|
GS |
222 |
189 |
26 |
437 |
222 |
378 |
78 |
678 |
313 |
|
678 = 6*113;
222:378:78 = 6*(37:63:13) |
|||||||||
364 ist zweimal die ZS von SATOR OPERA TENET des SATOR-Quadrats. Die auf die Numerierungssummen der 3 DR ausgerichteten Ergebnisse bestätigen die doppelte Punktestruktur der DR 313 und 314. 6*113 ist auf drei DR-Kreuze zu beziehen, da 6 DR erforderlich sind, wenn jede mit jeder ein DR-Kreuz bildet.
Die ZW/FW-Verrechnung stützt die Ergebnisse:
|
|
ZS |
FS |
sm |
|
|
678 |
313 |
991 |
|
FW |
118 |
313 |
431 |
|
sm |
|
|
1422 |
|
1422 = 27*79 > 87 = 3*29 |
|||
991 und 431 sind Primzahlen und nicht weiter zu verarbeiten. 431 entspricht wiederum der Gleichung von 4 = 3+1 Punkte zweier Rauten in der DR, die Einzelziffern von 1422 geben die Durchmesserelemente der beiden konzentrischen Tetraktyskreise wieder: 1+4 hexagonale und 2+2 Erweiterungselemente. 87 weist auf die 15 Rahmenelemente der DR hin, 3*29 auf drei DR-Kreuze.
6. Die ermittelten Numerierungssummen für die drei DR sind:
|
|
links |
|
Mitte |
|
rechts |
|
ZS |
FS |
GS |
|||
|
Fig.1 |
38 |
29 |
67 |
44 |
40 |
84 |
38 |
36 |
74 |
120 |
105 |
225 |
|
Fig.2 |
36 |
29 |
65 |
28 |
23 |
51 |
33 |
30 |
63 |
97 |
82 |
179 |
|
Fig.3 |
49 |
41 |
90 |
49 |
46 |
95 |
49 |
40 |
89 |
147 |
127 |
274 |
|
sm |
123 |
99 |
222 |
121 |
109 |
230 |
120 |
106 |
226 |
364 |
314 |
678 |
Die ZS+FS 226 der rechten DR bildet die numerische und symmetrische Mitte zwischen der linken und mittleren Raute. Wie 113 ist auch die doppelte Summe als Kontraktion der zweistelligen Zahlen 22+26 interpretierbar, sodaß sich aus 2*(11+13) ein Oktaeder zusammensetzen läßt.
In der Punkteaufteilung 1+(2+1+2)+1 der DR kommen auf jede DR 3+(6+3+6)+2 = 20 Punktezahlen, je 15 für den hexagonalen und 5 für den Erweiterungsbereich.
Eine
Besonderheit ist, daß die FS und ZS der 15 äußeren Kreislinienpunkte und der 20 Punkte der linken DR
jeweils 99 und 123 = 3*(33:41)
sind. Die 5 Zahlen, die beide gemeinsam haben, sind:
|
Zahl |
9 |
12 |
10 |
2 |
12 |
45 |
|
FW |
6 |
7 |
7 |
2 |
7 |
29 |
|
|
|
|
|
|
|
74 |
Das ZS+FS-Verhältnis
der gemeinsamen zu den nicht gemeinsamen Zahlen ist 74:148
= 74*(1:2). Somit besteht ein umgekehrtes Flächenverhältnis von äußerem
Kreisring zum hexagonalen Kreis. Weitere 5 Zahlen sind ebenfalls gemeinsam:
|
Zahl |
1 |
7 |
8 |
9 |
11 |
36 |
|
FW |
1 |
7 |
6 |
6 |
11 |
31 |
|
|
|
|
|
|
|
67 |
Das FS:ZS-Verhältnis der gemeinsamen Buchstaben ist 60:81 = 3*(20:27). Das
Verhältnis 20:27
ist auf 10+10 Maßeinheiten und 12 und 15 Punkte des zwei- und dreiachsigen Achsenkreuzes
zu beziehen. Die übrigen 5+10 Zahlen sind:
|
Zahl |
10 |
13 |
1 |
5 |
13 |
42 |
2 |
3 |
5 |
6 |
2 |
4 |
5 |
6 |
3 |
6 |
42 |
|
FW |
7 |
13 |
1 |
5 |
13 |
39 |
2 |
3 |
5 |
5 |
2 |
4 |
5 |
5 |
3 |
5 |
39 |
Dem FS:ZS-Verhältnis 39:42 =
3*(13:14) = (7:6)+(7:7) entsprechen die trinitarischen Kreisflächeneinheiten (1:2)+(1:3).
7. Ovid hat vier durch 13 teilbare ZS so geschickt geordnet, daß dreimal die gleiche ZS 157 und FS 113 zustande kommt. Sie entsprechen in ihrer Durchschnittseigenschaft drei DR. Ihre Addition ergibt jeweils 270 = FW 9+7 = 16. Es kann kein Zweifel bestehen, daß sich diese beide FW als Komplementärzahlen zu 1 und 3 auf 9 Durchmesserelemente der DR und 7 Elemente einer Tetraktysseite beziehen. Und so wie die drei Tetraktysseiten umfahren werden können, so ist dies auch bei den Rahmenelementen der DR möglich.
Die ZS+FS 270 repräsentiert einerseits eine einzelne DR, anderseits legt die Addition 270+16 = 286 = 2*(11*13) ein DR-Kreuz nahe, da aus 2*(11+13) Elementen der Raute und des sanduhrförmigen Doppeldreiecks ein Oktaeder zusammengesetzt werden kann. Auch die Einzelziffern in der Lesart 2*(8+6) weist auf zweimal 8 Rahmenlinien und 6 Binnenelemente der DR hin. 286 ist die ZS von zweimal PATERNOSTER. Hier noch einmal die Tabelle:
|
Zahl |
157 |
32 |
157 |
125 |
471 |
|
FW |
157 |
10 |
157 |
15 |
339 |
|
+13 |
170 |
23 |
170 |
28 |
391 |
Es liegt nahe, daß die dritte aufgeteilte DR Dädalus und Ikarus zugeordnet ist:
|
32 |
125 |
|
10 |
15 |
|
42 |
140 |
ZS+FW ergeben 182 = 13*14, die ZS von SATOR OPERA TENET – der Schöpfer erhält seine Werke. Nach Ovids Auffassung wird also auch der Mensch ein Werk Gottes, das von ihm im Dasein erhalten wird. Das Verhältnis der beiden ZS+FS ist 14*(3:10).
Dädalus und Ikarus verbinden sich jeweils mit einer ZS 157. F Es folgen die jeweiligen ZS und FS und ihre FW:
|
ZS |
sm |
FW |
SM |
FS |
sm |
FW |
SM |
GS |
||
|
157 |
32 |
189 |
16 |
205 |
157 |
10 |
167 |
167 |
334 |
539 |
|
157 |
125 |
282 |
52 |
334 |
157 |
15 |
172 |
47 |
219 |
553 |
|
314 |
157 |
471 |
68 |
539 |
334 |
25 |
339 |
214 |
553 |
1092 |
|
539:553 = 7*(77:79) = 7*156 = 7*12*13
= 13*84 = 4*273 |
||||||||||
Ovid hat das
Kunststück zustande gebracht, daß die 4Werte
einer jeden einzelnen DR-Verbindung
und die ZS+FW und FS+FW beider
jeweils gleich sind. Es wird so eine größtmögliche Einheit von Vater und Sohn
verdeutlicht. Auch die Summe 334
findet sich in jeder DR-Verbindung und die ZS 282 ist gleich der FW-Summe
68+214. Die Summe 219 ist die ZS+FS von DAEDALUS und ICARUS,
ihre Einzelziffern sind auch in der Gesamtsumme 1092 enthalten.
Die Einzelziffern der Faktoren 12*13 geben die beiden trinitarischen Kreisflächenverhältnisse der Tetraktyskreise wieder und werden durch den Faktor additiv zusammengefaßt. 273 = 13*21 ist die ZS des PATERNOSTER-Kreuzes. Die Faktoren 13+21 sind auf 13 hexagonale Elemente und auf alle 21 Elemente der DR beziehbar und geben das Kreisflächenverhältnis 1:3 wieder:
|
|
4*273 bedeuten demnach 2 DR-Kreuze.
77 und 79 sind die Konstitutivzahlen ihrer Summe 156. Die ZW/FW-Verrechnung zeigt wiederum die hohe Bedeutung der Zahl 97:
|
|
|
|
sm |
FW |
sm |
FW |
|
ZS |
79 |
77 |
156 |
20 |
|
|
|
FW |
79 |
18 |
97 |
97 |
|
|
|
sm |
117 = 9*13 |
253 |
117 |
370 |
44 |
|
|
FW |
253 = 11*23 |
34 |
19 |
53 |
53 |
|
|
sm |
|
|
|
|
|
97 |
Die Verrechnung führt zur Zahl 97 zurück. Die Zahl 156 stellt in der Aufteilung 15+6 die 15 Rahmenelemente und 6 Binnenelemente der DR dar.
Nun sind die Zahlen 157 und 156 konstitutiv für ihre Summe 313 und 79 ist komplementär zu 31 und 97 komplementär zu 13. Der FW sowohl von 77 und 78 ist 18 und führt in der Addition von 79 jeweils zu 97. Die plausibelste Erklärung ist, daß die 7 Punkte der DR die Aufgabe haben, einen Umlauf von 9 Positionen zu ermöglichen, um durch die Vereinigung der äußeren Punkte die Voraussetzung für die Oktaederbildung zu schaffen.
Auch die Verrechnung der zwei DR-Vereinigungen enthält den Faktor 97:
|
|
|
|
|
|
|
|
sm |
FW |
|
SM |
205 |
334 |
|
334 |
219 |
|
|
|
|
FW |
46 |
169 |
215 |
169 |
76 |
245 |
460 |
32 |
|
sm |
|
|
48 |
|
|
19 |
67 |
67 |
|
FW |
|
|
|
|
|
|
|
97 |
|
|
|
|
|
|
sm |
|
ZS |
205 |
334 |
334 |
219 |
1092 |
|
FW |
46 |
169 |
169 |
76 |
460 |
|
sm |
|
|
|
|
1552 |
|
1552 = 16*97 |
|||||
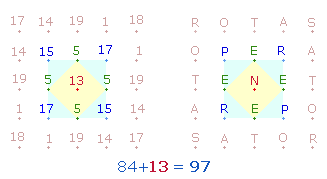
Auch die Addition der beiden Produktzahlen 84*13 ergibt 97. Sie sind die ZS des inneren SATOR-Quadrats:
|
|
Die Zahl 84 führt durch die Addition von 13 von der untersten zur obersten zweistelligen Umkerzahl.
Erstellt: April 2017, überarbeitet Februar 2018