Doppelzählung
der zwei Quadratrahmen
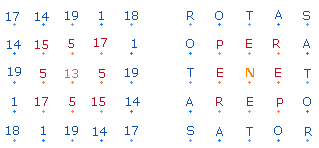
Die Quadratur des
Kreises im SATOR-Quadrat
I. Kreis und Quadrat
II. Grundlagen
der Doppelzählung
III. Doppelzählung
der zwei Quadratrahmen
I. Kreis und Quadrat
|
|
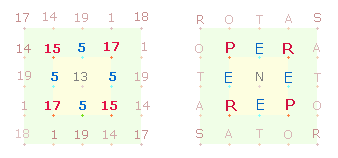
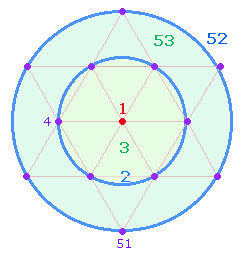
1. Eine Kreisfläche mit Lineal und Zirkel in ein Quadrat zu verwandeln, ist bekanntlich unmöglich. Redensartlich versteht man daher unter der Quadratur des Kreises eine unlösbare Arbeit. Auf einer anderen Ebene ist es jedoch genau das Ziel des SATOR-Quadrats (SQ), die Bedingungen des Kreises analog darzustellen. Ihre Gemeinsamkeit besteht in zwei konzentrischen Kreisen und Quadraten:
|
|
|
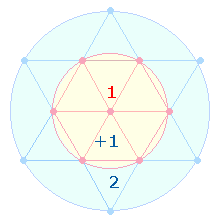
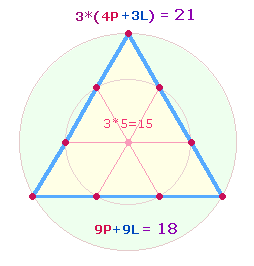
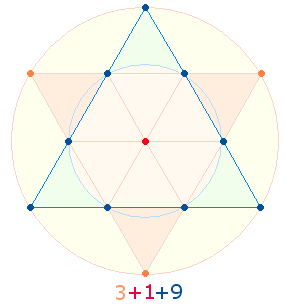
Der Durchmesser der beiden Kreise verläuft als Zickzacklinie, zwei
dieser Durchmesserlinien bilden eine Doppelraute (DR). Der
Durchmesser beider Figuren besteht aus 5:9 Elementen.
Die Kreisflächenverhältnisse betragen 1:2 und
1:3, die
Quadratflächenverhältnisse 1:3 und 1:4.
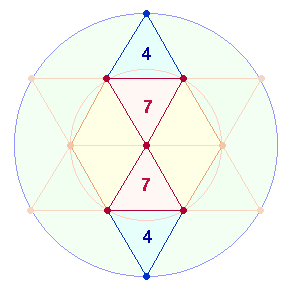
1. Die Zahlen 13 und 12 sind für beide Figuren von besonderer Bedeutung:
·
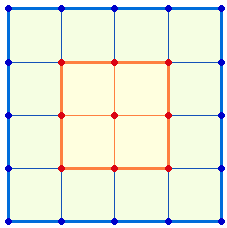
Das Hexagon und das innere Quadrat
bestehen beide aus 25 Elementen: Beide
enthalten 12 Linien, das Hexagon hat 7 Punkte + 6 Flächen, das Quadrat 9+4.
·
Der Tetraktysstern besteht aus 13 Punkten und 12
Dreiecksflächen.
·
Numeriert man die 25 Punkte der beiden Quadrate, sind 13 Zahlen ungerade, 12
gerade. Den 12 geraden Zahlen entsprechen die Vokale des SQ.
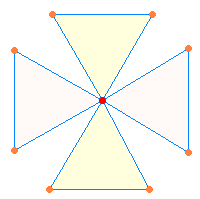
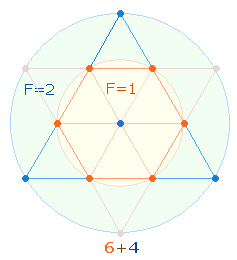
· Ein Achsenkreuz aus 2 Doppeldreiecken enthält 9
Punkte + 4 Dreiecke und 12 Linien und entspricht damit den Elementen des
inneren Quadrats:
|
|
2. Die Zahlensumme (ZS) + Faktorensumme (FS) des SQ beträgt 303+249 = 552 = 23*24. Eine Angleichung des SQ an die Kreisflächenverhältnisse 1:2 und 1:3 ergibt sich aus den FS des inneren Quadrats und des äußeren Quadratrahmens. Denn die FS des inneren Quadrats beträgt 83, die FS des äußeren Quadratrahmens 166 = 2*83. Die Primzahl 83 ist zu verstehen als Summe der Zahlen 1-7 = 28 und 1-10 = 55.
II.
Grundlagen der Doppelzählung
1. Grundlage von Doppelzählungen ist der KREISRADIUS. Der Radius ist eine Maßeinheit, die einen gleichen Abstand vom Mittelpunkt definiert. Definitionsgemäß ist der Kreis der Ort aller (potentiellen) Punkte, die vom Mittelpunkt gleichweit entfernt sind. 1 Maßeinheit ist definiert durch 2 Begrenzungspunkte. Eine Gerade, die den Mittelpunkt schneidet, erzeugt 2 Maßeinheiten, die in der Bezeichnung DURCHMESSER durch 3 Punkte begrenzt werden. 2 Maßeinheiten und 3 Begrenzungspunkte bilden demnach die 5 ELEMENTE des Durchmessers. Jede einzelne Maßeinheit (jede Radiallinie, jedes Radialmaß) beansprucht den Mittelpunkt für sich. So besteht also ein Durchmesser aus zwei Radialmaßen von je 3 Elementen, zusammen 6. Zwei Radialmaße bestehen demnach verbunden aus 5 und getrennt aus 6 Elementen. Dies ist das Ursprungsmodell der Doppelzählung: 4+3+4 und wohl auch innerer Zusammenhang zum Faktor 83 (s.o.) der FS 249 des SQ.
2. Das Prinzip der Verbundenheit und Getrenntheit setzt sich in den Flächenfiguren des Dreiecks und des Quadrats fort. Im gleichseitigen Dreieck und im Quadrat umschließen 3 und 4 zusammenhängende Maßeinheiten je 1 Element Fläche. Nun kann eine Dreiecks- oder Quadratseite aus mehreren Maßeinheiten bestehen. Um Art der Figur und Fläche zu kennzeichnen, werden bei Doppelzählung 3 oder 4 Eckpunkte dreifach, die übrigen Punkte und Linien zweifach gerechnet.
3. Im SQ wird der Mittelpunkt dem inneren Quadrat zugerechnet und nur einmal bei der Gesamtheit der Elemente berücksichtigt. In der folgenden Tabelle wird die Gesamtheit der Buchstaben gerechnet und die Zahl jeder Seite einzeln gezählt addiert:
|
Quadr. |
gesamt |
Seiten |
sm |
|
innen |
9 |
12 |
21 |
|
außen |
16 |
20 |
36 |
|
sm |
25 |
32 |
57 |
Den Summen 32 und 25 entsprechen die ZS und FS der inneren Eckbuchstaben PR:
|
|
4. Für die Konstruktion und Beschaffenheit des SQ sind folgende Gesichtspunkte von Bedeutung:
·
Die 4Werte
der Doppelzählung nach gesamt (G) und jeder
einzelnen Seite (S) der Elemente (E) des Dreiecks sind:
|
|
G |
S |
sm |
FW |
GS |
|
E |
7 |
10 |
17 |
17 |
34 |
|
FW |
7 |
7 |
14 |
9 |
23 |
|
|
14 |
17 |
31 |
26 |
57 |
Die 4W-Summe 57 stimmt mit der Doppelzählung der Buchstaben des SQ überein. Den 7 und 10 Elementen des Dreiecks entsprechen 7 hexagonale und 10 Tetraktyspunkte.
Die analogen 4Werte des Quadrats sind:
|
|
G |
S |
sm |
FW |
GS |
|
E |
9 |
13 |
22 |
13 |
35 |
|
FW |
6 |
13 |
19 |
19 |
38 |
|
|
15 |
26 |
41 |
32 |
73 |
Die ZS+FS 31 und 41 sind Primzahlen. Ihren Einzelziffern entspricht die Zahl der Seiten und je 1 Flächenelement. Das FS:ZS-Verhältnis ist (14+19):(17+22) = 33:39 = 3*(11:13).
In gematrischer Hinsicht sind 57 und 73 die ZS von PATER und FILIUS, ihre Summe 130 hat trinitarische Bedeutung.
·
Die Doppelzählung der Elemente
beider geometrischer Figuren ergibt 7+9 = 16 und 10+13 = 23. Den beiden Summen entspricht
der FW 16
der Zahl 39 = 3*13 und die Differenz 23
zur ZS 39. Nun sind die FS der Zahlen 1-16
und 1-23 die Umkehrzahlen 102+201 = 303, die ZS des
SATOR-Quadrats. 102
ist die ZS der 8 verschiedenen Buchstaben PENSATOR,
201 die ZS der 17
übrigen Buchstaben.
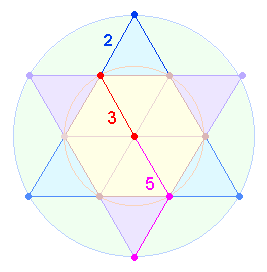
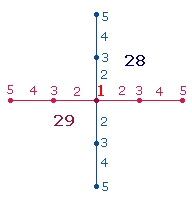
Die Umkehrung der Zahlen 102 und 201 läßt sich durch Kreisteilung und Numerierung der 3 Durchmesserpunkte darstellen:
|
|
·
Ebenfalls 39
ergibt die Doppelzählung des Tetraktysrahmens:
|
|
Hier stimmt die ZS+FS mit den 57 Buchstaben des SQ überein.
|
|
|
|
sm |
FW |
GS |
|
E |
18 |
21 |
39 |
16 |
55 |
|
FW |
8 |
10 |
18 |
8 |
26 |
|
|
|
|
57 |
24 |
81 |
Aus 81 Elementen bestehen die beiden konzentrischen Quadrate des SQ: aus 25 Punkten + 16 Quadraten und 40 Linien. Es besteht also eine innere Übereinstimmung zwischen den beiden Tetraktyskreisen und den zwei konzentrischen Quadraten, der die Urheber des SQ gerecht werden wollten. Es ist also zu vermuten, daß das SQ auf dem Prinzip der doppelten Zählung aufgebaut ist.
III.
Doppelzählung der zwei Quadratrahmen
1. Zu ermitteln sind zuerst die ZS+FS des inneren Quadrats und des äußeren Quadratrahmens und dann die ZS+FS jeder Seite beider Rahmen, wobei der Mittelpunkt bei der zweiten Zählung entfällt:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
i. Qu. |
97 |
83 |
180 |
97 |
83 |
180 |
360 |
|
ä. QR |
206 |
166 |
372 |
105 |
85 |
190 |
562 |
|
|
303 |
249 |
552 |
202 |
168 |
370 |
922 |
|
180:372 = 12*(15:31) |
|||||||
Die Summe der Zahlen von 1-30 beträgt 15*31 = 465. Der ZS+FS 180:552 = 732 = 12*61 entspricht das Flächenverhältnis 4:16 = 1:4. 61 ist die ZS des Wortes TENET.
Die ZS+FS der je vier Quadratseiten sind:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
i. QR |
148 |
120 |
268 |
41 |
14 |
55 |
323 |
|
ä. QR |
276 |
216 |
492 |
30 |
15 |
45 |
537 |
|
|
424 |
336 |
760 |
71 |
29 |
100 |
860 |
Die Eckbuchstaben SR-PR sind gegenüber der ersten Zählung doppelt zu rechnen, 26 für N abzuziehen: 120+114 = 234; 552-26 = 526; 526+234 = 760.
2. Die jeweils zusammengehörigen Summen sind:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
i. Qu./QR |
245 |
203 |
448 |
138 |
97 |
235 |
683 |
|
ä. QR |
482 |
382 |
864 |
135 |
100 |
235 |
1099 |
|
|
727 |
585 |
1312 |
273 |
197 |
470 |
1782 |
|
FW |
727 |
24 |
|
23 |
197 |
|
971 |
|
448:864 = 32*(14:27) = 32*41 |
|||||||
|
727+197 = 924
= 84*11 = 66*14; 585:273
= 39*(15:7) = 66*13 |
|||||||
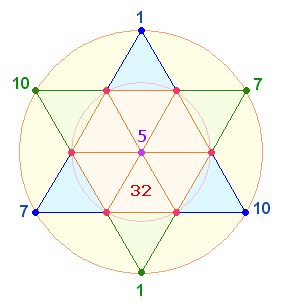
Die Gesamt-ZS+FS 1312 wird in den Einzelziffern den beiden Kreisflächenverhältnissen des Tetraktysstern gerecht als auch den oben genannten Additionen 13+12. 14 ist die Mittelpunktszahl von 27, 14*27 ergibt die Summe der Zahlen von 1-27.
Die Summe 32+41 = 73 läßt sich auf zwei numerierte Tetraktys beziehen:
|
|
32 beträgt die Summe der 6 hexagonalen Kreislinienpunkte, 2*18 = 36 der 6 Erweiterungspunkte und 5 der Mittelpunkt. Auf diese Weise ergibt sich die vollständige Numerierungssumme 2*55 = 110 aus den Umkehrzahlen 73+37.
Auffällig ist die zweimalige FW1/2-Summe 235 = 5*47 = FW 52. Die Einzelziffern geben zweimal 2*5 Radialelemente der DR wieder, ebenso die Einzelziffern von 32 und 41:
|
|
Der FW der 4W-Summe 1782 = 22*81 = 13+12 beträgt ebenfalls 25. Die Primzahl 2281 ist die FS der Zahlen von 1-100.
Durch Hinzufügung der FW-Summe 971 zur 4W-Summe 1782 ergibt sich die Primzahl 2753. Der Tetraktysstern besteht aus 2*24 symmetrischen Elementen. Zum Hexagon kommen hinzu die 3 Elemente Mittelpunkt, Kreisbogen und Kreisfläche, zum Erweiterungsbereich die 2 Elemente äußerer Kreisbogen und Kreisfläche, wobei die nochmalige Verwendung des Mittelpunktes nicht gezählt wird:
|
|
27:(27+26) Elemente geben demnach das Kreisflächenverhältnis 1:(1+2) = 1:3 wieder.
3. Durch Umgruppierung der 4Werte ergibt sich:
|
|
ZS |
FW-S |
sm |
FW |
sm |
FS |
FW-S |
sm |
FW |
sm |
GS |
|
|
727 |
273 |
1000 |
21 |
1021 |
585 |
197 |
782 |
42 |
824 |
1845 |
|
FW |
727 |
23 |
750 |
20 |
770 |
24 |
197 |
221 |
30 |
251 |
1021 |
|
|
|
|
1750 |
41 |
1791 |
|
|
1003 |
72 |
1075 |
2866 |
|
750:1000 = 250*(3:4) >24;
221:782 = 17*(13:46) >76; 24:76
= 4*(6:19) = 4*25 = 100 |
|||||||||||
|
21:42 = 21*(1:2); 20:30 = 10*(2:3) |
|||||||||||
Die von den umgruppierten Summen ermittelten FW 41+72 = 113 ergibt, zu 2753 hinzugefügt, 2866. 28 und 26 sind die Summen der Zahlen 1-7 und 1-11. Sie sind auf zwei Rauten der DR zu beziehen:
|
|
Eine Raute besteht aus 7 Elementen eines hexagonalen Dreiecks + 4 Erweiterungselementen: 7:(7+4) Elemente geben das Kreisflächenverhältnis 1:3 wieder. Dasselbe gilt für die Einzelziffern von zwei Summen 1021. Die Primzahl 1021 ist zusammensetzbar aus dem FW 10 der Zahl 21.
Übrig bleibt 824 = 64*13 = FW 12+13. Die Einzelziffern der Zahl 64 bedeuten ebenfalls, auf die 10 Tetraktyspunkte bezogen, das Flächenverhältnis 1:3:
|
|
IV. Zusammenhänge
1. Ein Kunstwerk entsteht immer unter den Bedingungen des Materials. Das Material ist dem freien Willen des Künstlers entzogen, es ist also frei vom Vorwurf der Willkür, sofern sie dem einen oder anderen Künstler angelastet wird. Es wurde in den vorausgehenden Ausführungen deutlich, daß die Doppelzählung kein Willkürakt ist, sondern den Figuren des Dreiecks und des Quadrats ontologisch eigen ist. Wenn also die Doppelzählung der ersten beiden konzentrischen Quadrate mit Mittelpunkt zur Summe 21+36 oder 25+32 = 57 führt, so erhebt sich die Frage nach der Bedeutung von 57 = 3*19.
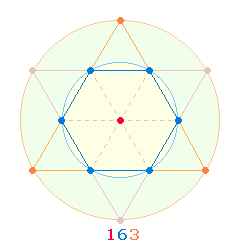
Die Zahl 19 setzt sich aus 8+1 Durchmesser- und 8+2 Radialelementen der DR-Zickzacklinie
zusammen. Das zweistellige Additionsergebnis 163 gibt in seinen Einzelziffern die Punkteaufteilung der
Tetraktys wieder, ebenso wie 319 die des Hexagramms:
|
|
|
Die Zahl 19 besteht also schon aus einer Dreifachzählung des
Mittelpunktes. Die Zahlen 10+9 können als Komplementärzahlen zu 1+2 angesehen werden. Als
Kardinalzahlen stellen sie einerseits das Flächenverhältnis des hexagonalen Kreises
zum Erweiterungsring dar, andererseits theologisch die drei göttlichen
Personen. Das Additionsergebnis 3+19 = 22 bezieht sich sinnvollerweise auf 2*11 Elemente der DR.
2. Die Summe der Zahlen von 1-7 ist 28. Nun befinden sich im Hexagon 3 sanduhrförmige Doppeldreiecke aus je 5 Punkten. Bei Numerierung der 7 Punkte vom Mittelpunkt aus wird dieser dreimal und die übrigen Punkte zweimal gezählt. Daraus ergibt sich 2*27+3 = 57.
57 ist auch
Numerierungssumme des Achsenkreuzes AK3:
|
|
Zur Vollständigkeit der Doppelzählung gehört die Numerierung der 7 Hexagonpunkte von 0-6. Die Summe der Zahlen von 1-6
= 21. Die beiden Zahlensummen 21 und 28 sind für die Doppelraute
von Bedeutung, da die 4*7 Elemente von vier Dreiecken 28 ergeben, die Zahl der Elemente
durch die Verbundenheit der Dreiecke jedoch auf 21 verkürzt ist. Die FW der beiden Numerierungssummen sind 11+10 = 21, so daß das FS:ZS-Verhältnis 21:49 = 7*(3:7). Der Verhältnisausdruck kann als 7 hexagonale : 10 Tetraktyspunkte
gelesen werden.
Die Numerierungssumme von 0-6 für die drei
Doppeldreiecke beträgt 2*21 = 42:
|
|
|
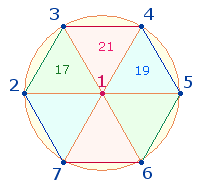
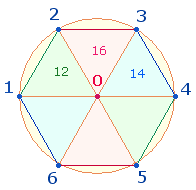
Die ZS+FS der
zwei Figuren betragen:
|
|
|
|
|
sm |
|
|
|
sm |
GS |
|
ZS |
17 |
21 |
19 |
57 |
12 |
16 |
14 |
42 |
99 |
|
FW |
17 |
10 |
19 |
46 |
7 |
8 |
9 |
24 |
70 |
|
sm |
|
|
|
103 |
|
|
|
66 |
169 |
|
169 = 13*13 = FW 26 |
|||||||||
Der FW 26 ist vornehmlich auf die 26 Elemente des Oktaeders zu beziehen, der sich aus einem DR-Kreuz zusammenfügen läßt. 13 Elemente einer DR lassen sich aus 7 Punkten und 6 Binnenelementen
zusammensetzen:
|
|
57 und 46 sind die FS der
Zahlen 1-10
und 1-11. 24:42, interpretierbar als 24:(24+18), bezieht sich auf die
Punkte und Linien von zwei Tetraktysrahmen, aus 6 Rauten von je 11 Elementen besteht der Tetraktysstern.
Zwei ZW/FW-Verrechnungen können die bisherigen Ergebnisse stützen:
|
|
|
|
sm |
FW |
sm |
FW |
|
ZS |
57 |
42 |
99 |
17 |
|
|
|
FW |
22 |
12 |
34 |
19 |
|
|
|
sm |
|
|
133 |
36 |
169 |
26 |
|
FW |
|
|
26 |
10 |
36 |
10 |
|
sm |
|
|
|
|
|
36 |
Das FW-Verhältnis 10:26 =
2*(5:13) könnte sich auf eine umlaufende
Numerierung der DR-Elemente beziehen, deren Mittelpunkt 5+13 bildet. 133 = 7*19 gibt in den Einzelziffern die 7 Punkte der DR wieder, 19 Punkten entsprechen 7 Kreisflächeneinheiten.
|
|
ZS |
FS |
sm |
FW |
|
|
99 |
70 |
169 |
26 |
|
FW |
17 |
14 |
31 |
31 |
|
sm |
|
|
|
57 |
Die Addition 26+31 = 57 entspricht der Doppelzählung der Dreiecks-Elemente (s.o.).
Die ZW/FW-Verrechnung der Umkehrungen 102 und 201 ergibt:
|
|
|
|
sm |
FW |
sm |
|
ZS |
102 |
201 |
303 |
104 |
|
|
FW |
22 |
70 |
92 |
27 |
|
|
sm |
|
|
395 |
131 |
|
|
FW |
|
|
84 |
131 |
215 |
|
395 = 5*79 >84 |
|||||
Wenn man DR-Kreuz
von 1-4 numeriert, ergibt sich für die 26 Elemente des Oktaeders die Summe 79:
|
|
MP |
Pu. |
Li. |
Fl. |
|
|
Häufigkeit |
1 |
5 |
12 |
8 |
26 |
|
Num.Zahl |
1 |
2 |
3 |
4 |
|
|
sm |
1 |
10 |
36 |
32 |
79 |
Die Zahl 5 ist als Volumen zu verstehen.
215 ist die Numerierung
der Kreisachse, wenn man im Mittelpunkt mit 1 beginnt und die Punkte rundum
numeriert.
Erstellt: Juli 2017