DAS SATOR-QUADRAT

BINNENSTRUKTUREN

I. Diagonalen des Quadrats

II. Teilung durch die Linien des Rautenquadrats

III. Die Zeilen 2-4

IV. Gematrische Summen struktureller Einheiten

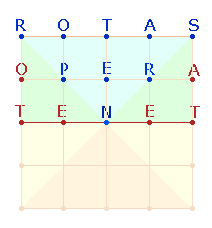
I. Diagonalen des Quadrats

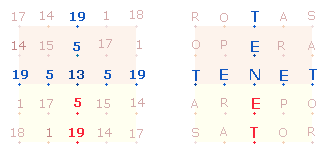
1. Die Diagonalen des SATOR-Quadrats teilen dieses in 4 gleiche Felder mit je 9 gleichen Buchstaben und gleicher ZS 119 = 7*17.

Multipliziert man die äußere und innere Quadratseite mit 4 und fügt 13 für das N hinzu, ergibt sich 4*(69+37)+13 = 437. Nimmt man 13 zum inneren Quadrat hinzu, erhält man das Verhältnis 23*(12:7). 7 ist gleichzeitig der Faktorenwert (FW) von 12.

2. Das durch die Diagonallinien eingefaßte Dreieck spart auf zwei Seiten je 3 Buchstaben aus, einen in Zeile zwei, zwei in Zeile drei. Das Verhältnis der Buchstaben der drei Dreiecke zueinander ist demnach 3*(1:3:1) bzw. der 9 Buchstaben des Diagonaldreiecks zu den 6 ausgesparten Buchstaben 3*(3:2):

Das ZS-Verhältnis der 9:6 Buchstaben ist 119:63 = 7*(17:9). Wenn man die 5 Buchstaben RPNRS auf den Diagonallinien den 6 Buchstaben der beiden kleinen Dreiecken zurechnet, bleiben die 4 Buchstaben OTAE übrig. Das ZS-Verhältnis der 4:11 Buchstaben ist 39:143 = 13*(3:11).

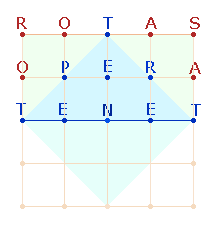
II. Teilung durch die Linien des Rautenquadrats

1. Die Linien des großen Rautenquadrats verlaufen in entgegengesetzter Richtung zu den Diagonallinien. Während die 4 Diagonaldreiecke alle Buchstaben erfassen, bleiben 4*3 Eckbuchstaben bei allen 4 Rautendreiecken ausgespart:

Auch hier gibt es zwei ZS-Verhältnisse, wobei die gemeinsamen Teiler in umgekehrter Folge auftreten: Die 9:6 Buchstaben haben das ZS-Verhältnis 117:65 = 13*(9:5), die 4 Buchstaben EEEN zu den übrigen 11 das Verhältnis 28:154 = 7*(4:22).

Der durchschnittliche ZW je Buchstabe des Rautendreiecks ist 13.

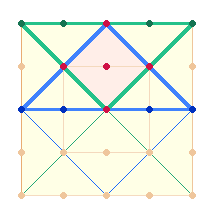
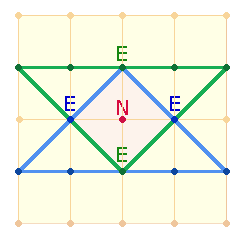
2. Die beiden gegenüberliegenden Dreiecke umgrenzen in der Mitte ein Rautenquadrat aus, dessen 5 Buchstaben die ZS 69 haben, die gleiche wie die Wörter SATOR/ROTAS:

Die beiden Dreiecke mit je 9 Punkten sind 2 Tetraktys vergleichbar. Die Punktefolge 1-3-5 entspricht der Anordnung der 9 Dreiecke in der Tetraktys.

Eine Tetraktys besteht aus 37 Elementen, der Tetraktysrahmen aus 3*7 Elementen (bei Zählung jeder Seitenlänge). Die ZS der 9:6 Buchstaben ergeben jeweils die FS 37: 119>24, 63>13 und 117>19, 65>18.

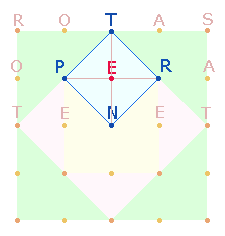
Das eingerahmte Rautenquadrat aus 5 Punkten hat die ZS 32+5 je Achse (PER, TEN):

Die ZS 37 je Achse entspricht der Numerierung der Tetraktys mit der Summe 32 für die 6 Punkte des Hexagonrahmens und der Zahl 5 für den Mittelpunkt.

Die 4 Eckpunkte des umgrenzten Rautenquadrats haben dieselbe ZS 64 wie die 4 Eckpunkte des inneren Quadrats (RPRP).

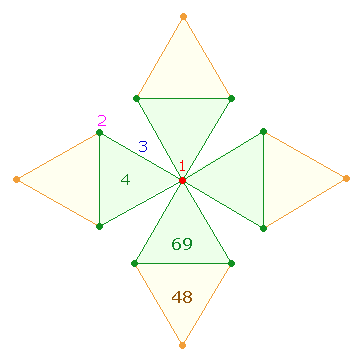
3. Die ZS des Rautenquadrats und der diagonalen Dreiecke weisen indes auch auf das Doppelrautenkreuz, das sich zu einem Oktaeder zusammengefügen läßt. Wenn man den Mittelpunkt mit 1, die übrigen Punkte mit 2, die Linien mit 3 und die Dreiecksflächen mit 4 numeriert, ergibt sich für die 25 Elemente des hexagonalen Kreuzes die ZS 69 und für die 16 Erweiterungselemente die ZS 48. 69+48 = 117 beträgt die ZS des Rautenquadrat-Dreiecks:

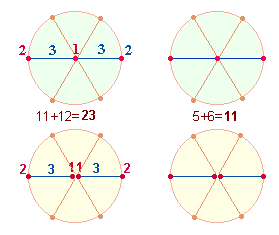
Die ZS 69 von SATOR wurde durch die gleiche Numerierungsordnung für die drei Hexagonachsen ermittelt, wobei sowohl die Durchmesser- als auch die Radialelemte gezählt wurden: 3*(11+12) = 69. Ebenso sind in einem zweiten komplementären DR-Kreuz der zweiten Doppelraute (DR) zwei Mittelpunkte zuzuordnen. Diese sind in der ZS 119 des diagonalen Dreiecks berücksichtigt.

Die ZS einer einzelnen numerierten DR beträgt für den hexagonalen Bereich 35, für den Erweiterungsbereich 24. Den beiden ZS entsprechen die Buchstaben RS und TE, woraus sich TRES – drei bilden läßt. Ein theologischer Bezug ist anzunehmen. Im diagonalen Dreieck bleiben die Buchstaben AO (15) und PRN (45) übrig; ihr ZS-Verhältnis ist 15*(1:3).

III. Die Zeilen 2-4

1. Die gegenläufigen Dreiecke der Zeilen 1-3 können für die Zeilen 3-5 wiederholt werden. Die Zeilen 2-4 dienen als Verbindung der zwei Quadrathälften. Eine Möglichkeit hierfür sind wiederum zwei Dreiecke, die ein Rautenquadrat aussparen:

Von der ZS 165 der drei Zeilen sind 2*19 für zwei T abzuziehen und es bleibt 127.

Die ZS des zentralen Achsenkreuzes ist 33. Die Achsenendpunkte sind jeweils vom Buchstaben E besetzt. Die Achsenkreuze beider Rautenquadrate sind darin innerlich verbunden, daß die ZS jeder Achse gleich ist, vom oberen und unteren beträgt sie jewels 37, vom mittleren 23.

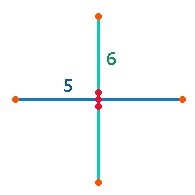
2. Die ZS 69 von SATOR wurde bereits erklärt als Summe von numerierten Durchmesser- und Radialelementen. In nicht-numerierter Form beträgt die Summe je Achse 5+6 = 11, für drei Achsen 33:

In den beiden Rautenquadraten des SQ ist die Symmetrie der Achsen gewahrt wie im Hexagon. Der Doppelaspekt von DM- und Radialelementen kann durch ein Achsenkreuz wiedergegeben werden, dessen zweite Achse zwei Mittelpunkte enthält. Diese Grundidee ist im SQ offenbar verwirklicht:

Der ZS 33 des inneren Quadrats entspricht die ZS der drei Buchstaben PEN, die mit den 5 Buchstaben des Wortes SATOR die 8 unterschiedlichen Buchstaben des Quadrats ausmachen. Zusammengesetzt ergibt sich das Wort PENSATOR – der, der abwiegt und im Gleichgewicht hält.

Man wird den beiden Achsenkreuzen (Rautenquadraten) also dadurch gerecht, daß man die ZW ihrer Buchstaben zweimal zählt, einmal 5 und einmal 3+3:

RQ	5 Bu.	3+3 Bu.		sm
außen	69	37	37	143
Mitte	33	23	23	79
sm	102	120		222
222 = 6*37

Die Gesamtsumme 222 enthält wiederum die Zahl 37 als Durchschnittswert der 6 Zählungen. Da eine Tetraktys aus 37 Elementen besteht, kann sie ihren Anfang von jedem der 6 Eckpunkte des Tetraktyssterns nehmen.

Nun ist das äußere Rautenquadrat oben und unten (links und rechts) vertreten. Man muß zur Summe 222 noch einmal 143 hinzuzählen und erhält 365 = 5*73. Die Hinzufügung der ZS 143 bewirkt also ein Umkehrung des Faktors 37 zu 73 wie auch die Buchstaben des Quadrats. Die Gesamtsumme 365 enthält in ihren Einzelziffern die 3 Achsen des Hexagons und den Doppelaspekt von 6 Radialelementen + 5 DM-Elementen.

3. Die beiden mittleren Dreiecke haben jeweils dieselbe ZS 80. Einmal 80+33 = 113 ist derselbe Wert wie OPERA (52) TENET (61). 80+33+80 ergibt die Zahl 193, deren Einzelziffern die Aufteilung der 13 Punkte der Tetraktys wiedergibt.

IV. Gematrische Summen struktureller Einheiten

1. Eine Einheit aus zwei gegenläufigen Dreiecken und einem Rautenquadrat umfaßt 9+5+9 = 23 Buchstaben. Die drei ermittelten Einheiten (oben, Mitte, unten) führen somit wiederum zum ZS 69 von SATOR/ROTAS. Teilt man die Buchstabenzahlen in (5+4) + (5+9) auf und bezieht sie auf die 9 DM-Elemente des Tetraktyssterns, geben sie das Flächenverhältnis 3:4 der beiden konzentrischen Kreise wieder.

2. Es gibt im SQ zwei Gliederungen des Außen und Innen und ihrer Verklammerung: die der Buchstabenzeilen als ganze und diagonale Gliederungen. Das Muster der ersteren ist 2-3-2, der zweiten 3-3-3.

Die ZS der beiden äußeren Zeilen ist 2*(69+52) = 22*11, die der drei mittleren 52+61+52 = 15*11, zusammen 37*11. Die ZS der diagonalen Gliederungen führen zu folgendem Ergebnis:

	3ecke		RQ	sm
außen	119	117	69	305
innen	80	80	33	193
außen	117	119	69	305
sm	316	316	171	803
803 = 73*11

Von den Rautenquadraten sind nur 5 Buchstaben berechnet, also nicht die Buchstaben jeder Achse.

Die Summen beider Gliederungen sind durch 11 teilbar und haben als zweiten Faktor die Umkehrzahlen 37 und 73, zusammen 11*110 = 1210 = 10*11².

Die Differenz der FS zu ihren ZS ist für die äußeren diagonalen Gliederungen (Dreieck u. Rautenquadrat) 2*(29+7) = 2*36, für die beiden inneren Dreiecke mit Rautenquadrat 2*12, sodaß sich zweimal das Differenzverhältnis 12*(1:3) ergibt. Die Differenz der äußeren Zeilen ist 2*27 = 54, das der Mittelzeilen 24. Das Differenzverhältnis für die beiden Gliederungen ist somit 96:78 = 6*(16:13) = 174. Die ZS+FS in tabellarischer Darstellung:

	Zeilen			diag.Gl.
	ZS	FS	sm	ZS	FS	sm	GS
außen	242	188	430	610	538	1148	1578
innen	165	141	306	193	169	362	668
sm	407	329	736	803	707	1510	2246
2246 = 2*1123
329:707 = 7*(47:101) = 7*148 = 28*37

Die Primzahl 1123 enthält in den Zahlen 11 und 23 den Doppelaspekt der unnumerierten und numerierten DM- und Radialelemente.

3. Der Doppelaspekt 5+6 = 11 der RQ und des gesamten SQ wurde bisher nicht berücksichtigt und kann in Beziehung gesetzt werden zu den Verklammerungsstrukturen:

	Bu.	ZS	FS	sm
SQ 5+6	55	667	559	1226
RQ 5+6	33	365	323	688
sm	88	1032	882	1914
2-3-2	35	407	329	736
3-3-3	54	632	550	1182
sm	89	1039	879	1918
GS	177	2071	1761	3832
2071 = 19*109

Auffällig sind die sehr nahen Ergebnisse der beiden Gruppierungen. Die FS 882 und 879 beispielsweise bilden das Verhältnis 3*(294:293) = 3*587.

Die ZS 19*109 weist auf das TENET-Kreuz hin, das sowohl 4 T enthält als auch die ZS 109 hat. 9*19 = 171 beträgt die ZS der drei Rautenquadrate (69+33+69), sodaß noch 100*19 = 1900 übrig bleibt.

Die erste Gruppierung enthält 10+4 = 14 T, die zweite 4+6 = 10 T, zusammen 24 T. Die ZS 85 umfaßt eine Hälfte des TENET-Kreuzes und es bleibt ET = 24 übrig:

4. Die Zahlen und Summen der Tabelle sind als bedeutsam anzusehen, auch wenn es nicht so scheint und es schwierig ist, ihren wahren Stellenwert zu ermessen. Sie sind generell auf die Grundlagen des Dezimalsystems (9 und 10) und dessen geometrische Modelle ausgerichtet, wobei möglichst alle vereint werden, also die Zweiheit und die Dreiheit, drei Achsen und zwei Achsen, das Dreieck und das Quadrat, und insbesondere der Oktaeder.

In zweistelliger Zusammensetzung enthalten die Summen 1914 und 1918 Buchstaben des SQ: TO und TS, die man zu TOST- gruppieren kann, dem Partizip Perfekt zu TORRERE – trocknen, rösten. Möglicherweise kann ein Zusammenhang zum VESTA-Kult hergestellt werden. Die Zahlen 19 und 18 verweisen auf die 37 Elemente der Tetraktys, aber haben noch eine weitere Bedeutung, wie noch zu zeigen sein wird.

Ein aussagefähiges Ergebnis liefert die ZW/FW-Verrechnung:

			sm	FW	Fkt.
ZS	1914	1918	3832	485	8*479
FW	45	146	191	191
sm	6*11*19	14*137		676
676 = 26*26

Das quadratische Produkt 26² verweist auf das DR-Kreuz und den Oktaeder mit 4 Doppeldreiecken aus je 13 Elementen. Die FW 67+23 der Umkehrzahlen 67 und 76 ergeben 90 = 10*9 und haben so besonderen Bezug zum Dezimalsystem.

5. Den 89+88 Buchstaben entspricht ein numeriertes Achsenkreuz AK5:

6. Die ZS+FS einer anderen Kombination ist ebenfalls durch 109 teilbar:

	Bu.	ZS	FS	sm
SQ 5+6	55	667	559	1226
2-3-2	35	407	329	736
sm	90	1074	888	1962
3-3-3	54	632	550	1182
RQ	33	365	323	688
sm	87	997	873	1870
GS	177	2071	1761	3832
1962 = 18*109

Da 90 Buchstaben 18 Buchstabenzeilen bedeuten, ist die durchschnittliche ZS+FS je 5 Buchstaben 109.

V. Einzeluntersuchungen

1. Aus Gründen der Differenzierung erscheint es angebracht, die Summen 1914 und 1918 in zusammengehörige Teile aufzugliedern. Bei der ersten Summe geht es um die ungerade Zahl 5 und die Hälften 3+3 des SQ und der 3 kleinen RQ:

	5			3+3
	SQ	RQ	sm	SQ	RQ	sm	GS
ZS	303	171	474	364	194	558	1032
FS	249	157	406	310	166	476	882
sm	552	328	880	674	360	1034	1914
880:1034 = 22*(40:47); 882:1032 = 6*(147:172)
474:558 = 6*(79:93)

Die ZS+FS der beiden Teile sind jeweils durch 22 teilbar. Die Differenz zwischen FS und ZS beträgt 6*25 = 150.

Bei der Summe 1918 geht es um die beiden äußeren Teile und den Innenteil:

	außen			innen
	Zeil.	3ecke	sm	Zeil.	3ecke	sm	GS
ZS	242	472	714	165	160	325	1039
FS	188	414	602	141	136	277	879
sm	430	886	1316	306	296	602	1918
1316:602 = 14*(94:43); 602:714 = 14*(43:51)

Die ZS+FS der beiden Teile sind jeweils durch 14 teilbar. Die Differenz zwischen der FS 879 und der ZS 1039 beträgt 160. Die Differenzsummen von außen und innen sind 112:48 = 16*(7:3). Die Differenzsummen 150 und 160 der beiden Tabellen bilden das Verhältnis 10*(15:16).

Beachtenswert ist die Summe 1316 = 4*7*47. Aus 13+16 läßt sich der Rahmen eines DR-Kreuzes bilden:

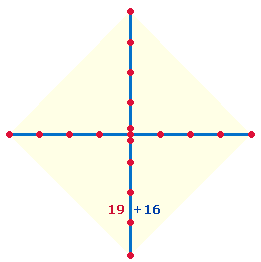
2. Die Mitte zwischen 1914 und 1918 ist 1916. Den Zahlen 19 und 16 entspricht ein Achsenkreuz AK5 mit 3 Mittelpunkten, sodaß es in 19 Punkte und 16 Linien aufgeteilt ist:

Diese Bedeutung wird gestützt durch die Faktoren 4*479. Die Zahl 479, aufgeteilt in 4+7 und 9, weist auf zwei Achsenkreuze aus 11 und 9 Elementen hin:

Wie schon oben dargelegt, stellt das zweite Achsenkreuz den Doppelaspekt von 5 DM- und 6 Radialelementen der Kreisachse und ein strukturelles Prinzip des SQ dar. Die beiden Radialmaße werden zweimal gezählt.

Wie ich bereits in einem früheren Beitrag ausgeführt habe, bilden die Zahlen 14-18 eine Einheit, denn die beiden Randzahlen sind zu interpretieren als 1+4 und 1+8 DM-Elemente des Hexagons und des Tetraktyssterns. Die Zahl 1918 umfaßt in ihren Einzelziffern sowohl die 10 Radialelemente als auch die 9 DM-Elemente.

Die ZW/FW-Verrechnung der 5 Zahlen liefert folgendes Ergebnis:

						sm	FW	sm	FW
Zahl	1914	1915	1916	1917	1918	9580	488
FW	45	388	483	80	146	1142	573
sm		5*383				10722	1061		9*317
FW						1792	1061	2853	323

Aufschlußreich ist der Faktor 383 der Zahl 1915, die Radialelemente der beiden Tetraktyskreise enthält und sich auf die 3 Hexagonachsen, 8 Symmetrieelemente und 3 Mittelpunkte beziehen läßt:

Der FW 323 besteht aus den Primfaktoren 17 und 19, hat also Bezug zu der zusammengesetzten Zahl 1917. In der Aufteilung 32+3 gelangt man wieder zum bereits gezeigten Achsenkreuz aus 35 Elementen. Aus 17 und 19 Elementen bestehen zwei komplementäre Achsenkreuze des AK3:

Erstellt: Dezember 2005

Überarbeitet: Januar 2011, Mai 2016

Inhalt

Startseite SQ