Die Zahlensummen der Zeilen 2-4 als Faktorensummen in der
Doppelraute
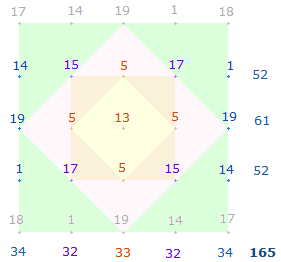
Die Zahlensummen (ZS) des SATOR-Quadrats sind 69-52-61-52-69. Die Addition der 1. u. 2. bzw. 4. u. 5. Zeile ergibt 121= 11*11. Die 2. bis 4. Zeile ist mit der Summe 165
ebenfalls durch 11
teilbar: 15*11. Die Quadratzahl 121 wird sichtbar, wenn man die erste Zahl 1 und die letzte Zahl 21 nebeneinander stellt.
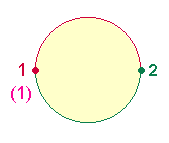
Die Zahl 21 schließt gewissermaßen einen Kreis, weil sie die Umkehrung der
ersten beiden Zahlen 1 und 2 in zwei Kreisbogenhälften darstellt:
|
|
Die Summe der Zahlen von
1 bis 21 ist 11*21 = 231. Die Faktorensumme ist ebenfalls durch 11 teilbar und beträgt 165.
|
|
Die Zahl 21 ist die Summe der Zahlen von 1 bis 6: 1+2+3+4+5+6. Konzentrisch gehören zusammen 1+6, 2+5, 3+4. Die ersten beiden
Zahlen bilden in ihrer Umkehrung 52, 61, 52, die Zahlenwerte der
Zeilen 2-4.
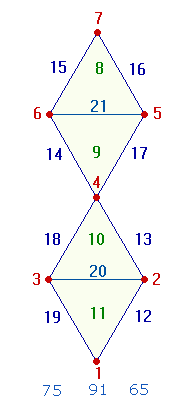
Eine Doppelraute besteht
aus 21 Elementen, 7 Punkten, 10 Linien und 4 Dreiecken.
|
|
|
Die linke
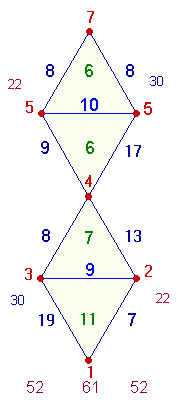
Doppelraute enthält die Zahlenwerte, die rechte die Faktorenwerte.
Die Zahl 21 setzt sich aus 11+10 zusammen. Für das
Dezimalsystem sind die 10 Zahlen von 12-21 von besonderer Bedeutung. Daher ist es sinnvoll,
zuerst die 7
Punkte und 4
Dreiecke zu numerieren und ab der Zahl 12 mit den 10 Linien weiterzufahren.
Die
Anordnung der Zahlen erfolgt auf folgende Weise: Man beginnt mit der
Numerierung der Punkte von unten nach oben in Zickzackform und kehrt über die 4 Dreiecke zum Ausgangspunkt
zurück. Dann umfährt man die 8 Linien in Schleifenform und numeriert zum Abschluß die
beiden Querlinien von unten nach oben.
Die
Umkehrung 12:21 geschieht dadurch, daß zu der Zahl 12 die Zahl 9 hinzugefügt wird und das Verhältnis
des Teils zum Ganzen gebildet wird. Die Doppelraute hat auf der linken und rechten Seite
je 2*3 Elemente aus Linie, Punkt, Linie. Die vertikale Linie besteht aus 3 Punkten, 4 Dreiecken und 2 Querlinien. Das
Verhältnis der 3 Zahlenreihen ist 6:9:6 = 3*(2:3).
Die 4*3 Einheiten zeigen 2
verschiedene Faktorensummen 22 und 30, so daß sowohl vertikal als auch horizontal je 2*3 Einheiten die Summe 52
ergeben. Die 9
Werte der Mittelvertikale haben das Additionsergebnis 61.
Die
zweimal gleiche Aufteilung von 22
und 30 ist erstaunlich. Sie weist auf
zwei Darstellungsweisen von 10
Maßeinheiten hin:
– auf zwei
Achsenkreuze, deren 10
Maßeinheiten durch 12
Punkte begrenzt werden:
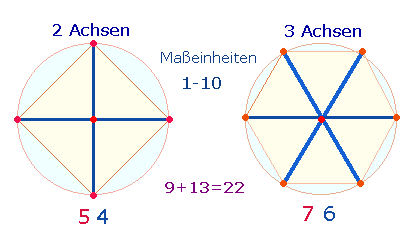
– In fortlaufender
Numerierung kann jede Maßeinheit durch eigene Punkte begrenzt werden. Auf diese
Weise entstehen 10*3 = 30
Einheiten. Diesem
Thema ist
eine eigene Untersuchung gewidmet.
Die Primzahl 139 steht besonders für die beiden
Achsenkreuze und ergibt sich aus der ZW/FW-Verrechnung:
|
|
FS |
sm |
FW |
sm |
|
|
|
22 |
30 |
52 |
17 |
|
|
FW |
13 |
10 |
23 |
23 |
|
|
sm |
|
|
75 |
40 |
115 |
|
FW |
|
|
13 |
11 |
24 |
|
sm |
|
|
|
|
139 |
Erstellt:4. 12. 2004
Letzte Änderung: Dezember 2010