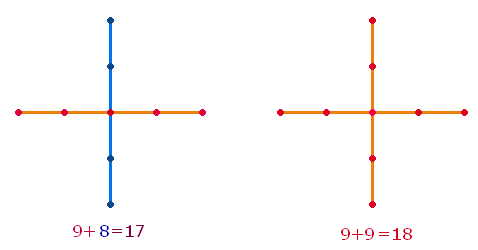Das Buchstaben- und Zahlenmodell
VESTA
Drei konzentrische Zusammensetzungen der Zahlen 1-20
1. Die
konzentrische Betrachtungsweise der Zahlen 1-20 zeigt
sich in der Form der drei lateinischen Buchstaben (AV)X. Denn X als 21. Buchstabe des lateinischen
Alphabets erscheint zusammengesetzt aus A und V als 1. und 20. Buchstabe. Die Gleichung A+V=X als
mathematische Verdoppelung ist in der Perfektform AVX-I – ich habe
vermehrt sinnentsprechend verdeutlicht.
2. Das Modell VESTA mit der
Zahlensumme (ZS) 63 = 3*21 bildet drei Doppelrauten des
Tetraktyssterns, bestehend aus jeweils 21 Elementen, durch konzentrische
Addition von 20+1, 19+2, 18+3 ab:
|
ZW |
1 |
2 |
3 |
4-17 |
18 |
19 |
20 |
|
Bu. |
A |
E |
|
S |
T |
V |
|
3. Das
Zahlensystem ist in sich so stimmig, daß die genannten Additionen auch als
dreistellige Zusammensetzungen sinnvolle Ordnungen ergeben. Diese zeigen sich
in Verbindung mit den Faktorenwerten (FW):
|
ZW |
FW |
sm |
ZW |
FW |
sm |
GS |
GS |
GS |
|
201 |
70 |
271 |
120 |
14 |
134 |
321 |
84 |
405 |
|
192 |
15 |
207 |
219 |
76 |
295 |
411 |
91 |
502 |
|
183 |
64 |
247 |
318 |
58 |
376 |
501 |
122 |
623 |
|
576 |
149 |
725 |
657 |
148 |
805 |
1233 |
297 |
1530 |
|
297:1233 = 9*(33:137) =
9*170 |
||||||||
Die Faktorensumme (FS) 297 setzt sich aus ihren
benachbarten Konstituenten 149+148 zusammen. Sie ist wie die Zahlensummen (ZS) durch 9 teilbar.
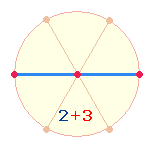
Die ZS+FS 805 = 5*(7*23) und 725 = 25*29 sind jeweils durch 5 teilbar. Darin zeigt
sich die enge Zusammengehörigkeit der Zahlen 2+3. Die Zahleneinheit 5 hat ihr geometrisches
Modell insbesondere in zwei Radialmaßen und drei Punkten des Kreisdurchmessers:
|
|
4. Die ZS und FS ergeben
Zahlenverhältnisse, in der Gruppierung zweimal drei:
|
ZW |
FW |
sm |
ZW |
FW |
sm |
|
|
201 |
70 |
271 |
183 |
64 |
247 |
|
|
120 |
14 |
134 |
318 |
58 |
376 |
|
|
192 |
15 |
207 |
219 |
76 |
295 |
|
|
513 |
99 |
612 |
720 |
198 |
918 |
|
|
612:918
= 306*(2:3) = 5*17*18 |
||||||
|
513:720 = 9*(57:80) |
||||||
|
99:198 = 99*(1:2) |
||||||
Die Verhältniszahlen 1:2 und 2:3 können auf die
Kreisachse bezogen werden: auf 3 Radialelemente aus 1 Radialmaß und 2
Begrenzungspunkten und auf 5 Durchmesserelemente aus 2 Radialmaßen und 3
Begrenzungspunkten.
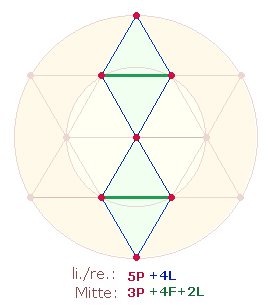
5. Die FS 297 = (3*9)*11 kann verschieden
gedeutet werden. Eine Deutungsmöglichkeit bezieht sich auf die Doppelraute.
Zwei Zickzacklinien besteht aus je 9 Elementen, zu denen noch ein
Mittelteil aus 9 Elementen hinzukommt:
|
|
Aus 11 Elementen besteht eine
Doppelraute.
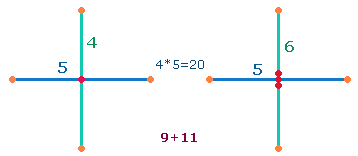
6. Die
gemeinsamen Teiler 306 = 18*17 und 99 = 9*11 weisen
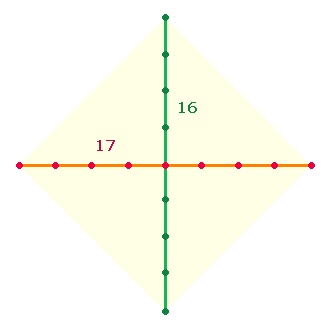
auf drei Achsenkreuzgrößen (AK), in denen die Zahl 5 eine sich ausdehnende Rolle
spielt: Die Zahl 5 kann
bestehen aus
– 3 Punkten + 2 Linien der Kreisachse (AK2),
– 3 Punkten + 2 Linien eines Achsenarms (AK3),
– 5 Punkten
eines Achsenarms (AK5).
Damit auch die
Radialelemente berücksichtigt werden, ist jeweils ein zweites Achsenkreuz und
eine zweite Achse mit zwei Mittelpunkten zu denken oder zwei Achsen mit
derselben Zahl von Elementen:
|
|
|
|
|
|
|
Das Achsenkreuz 17+18 ist Grundlage des SATOR-Quadrats.
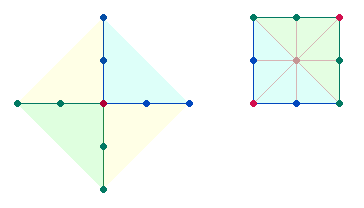
7. Die Zahlen 20 und 17
sind besonders von Bedeutung für das Quadrat, das aus einem AK3 durch Winkelverschiebung
entsteht:
|
|
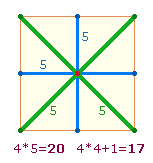
Das aus dem AK3 entstandene Quadrat
besitzt 4
Achsen zu je 5
Elementen. Wenn der Mittelpunkt nur einmal gerechnet wird, entfallen drei Mittelpunkte
und die Zahl der Elemente wird von 20 auf 17 reduziert:
|
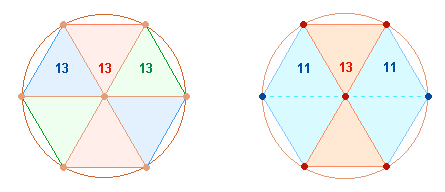
8. Die FW der ZS+FS 805 und 725 sind 39 und 35. Sie
entsprechen den Summen von zwei Figurenkonstellationen des Hexagons:
|
|
Erstellt: November 2012