Ordnungen der Zahlen 1-21
A. Ordnungen im
Tetraktysrahmen
B. Ordnungen in
linearer Abfolge
1.
Die Bedeutung
der Zahlen 1-21 liegt darin, daß auf einer
linearen Strecke 10 Maßeinheiten einer
Begrenzung durch 11 Punkte bedürfen:
|
|
8+2
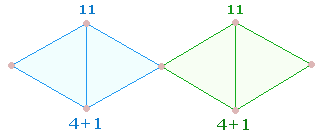
Maßeinheiten enthält auch die Doppelraute, 8
auf dem Rahmen + 2 Querlinien:
|
|
2.
Kennzeichnend für
die Zahlen 1-21 ist das Verhältnis der Faktorensumme (FS)
zur Zahlensumme (ZS) 165:231 = 33*(5:7).
|
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
231 |
|
FW |
1 |
2 |
3 |
4 |
5 |
5 |
7 |
6 |
6 |
7 |
11 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
10 |
165 |
Eine Tetraktysseite besteht aus 7 Elementen: 4
Punkten und 3 Linien. Den Faktoren 3*7 entsprechend lassen sich die Zahlen 1-21 auf dem Tetraktysrahmen anordnen:
|
|
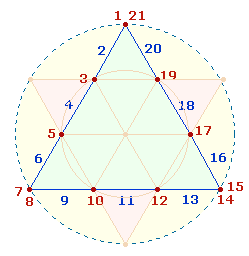
Aufgrund konzentrisch-symmetrischer Anordnung
ergänzen sich je zwei Zahlen horizontal zu 22 =
2*11: 1+21 = 22, 2+20
= 22 usw. In Beziehung zu setzen sind die Zahlen und Faktorenwerte (FW) auf den Punkten
und den Linien:
Die Zahlen der Punkte bauen sich in 4 Ebenen auf. Auf jeder Ebene ergibt sich für je
zwei Zahlen eine durch 11 teilbare FS: 1+10 = 11, 2+9 =
11 usw. Die ZS und FS der Ebenen 2
und 3 sind gleich, da die vier Zahlen
Primzahlen sind. Die folgende Tabelle zeigt FS
und ZS geteilt durch 11
sowie die fortlaufenden (fl.) Verhältnisse:
|
Eb. |
FS |
ZS |
Verh. |
|
1 |
1 |
2 |
1:2 |
|
2 |
2 |
2 |
3:4 |
|
3 |
2 |
2 |
5:6 |
|
4 |
4 |
6 |
9:12 |
Das FS:ZS-Verhältnis der Punktezahlen
ist 11*(9:12) = 33*(3:4) = 99:121 = 231. Somit kann gesagt werden, daß die ZS+FS 231 der auf den Punkten angeordneten Zahlen gleich
der ZS 231 der Zahlen 1-21
ist und die ZS+FS
165 der auf den Linien angeordneten gleich
der FS 165 der Zahlen 1-21.
3.
Die Ordnung der
Linienzahlen ist komplexer. Durch 11 teilbar ist zunächst die Symmetriemitte 11 selbst. Die FS 11
ist dreimal aus folgenden Kombinationen möglich: 2+20
(2+9), 6+9 (5+6), 2+4+6 (2+4+5), weiterhin durch die Umkehrsummen 12+21 = 3*11
aus 4+18 (4+8=12)
und 13+16 (13+8=21).
Diese Situation läßt sich etwa so darstellen:
|
|
FS:11 |
ZS |
V. |
V.fl. |
|
2+20 |
1 |
22 |
1:2 |
1:2 |
|
11 |
1 |
11 |
1:1 |
2:3 |
|
6+9 |
1 |
15 |
4:6 |
6:9 |
|
4+18+16+13 |
3 |
51 |
Das FS:ZS-Verhältnis der Linienzahlen
ist 11*(6:9) = 33*(2:3) = 165.
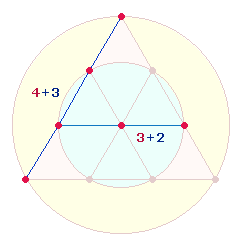
Faßt man die ersten drei Ebenen (6 Zahlen) zusammen
und setzt sie in Beziehung zur vierten (3 Zahlen), ergeben sich für die Linienzahlen folgende Werte:
|
Eb. |
1-3 |
4 |
|
ZS |
66 |
33 |
|
FS |
36 |
30 |
Das FS-Verhältnis
der beiden Gruppen ist 6*(6:5). Das FS:ZS-Verhältnis
ist 6*(6:11) und 3*(10:11).
4.
Die beiden FS:ZS-Verhältnisse
3:4 und 2:3 lassen sich zunächst auf die Elemente einer
Tetraktysseite und einer Kreisachse beziehen:
|
|
Das Differenzverhältnis zwischen FS und ZS ist 3:1 und 2:1. Diese
Verhältniszahlen mit der Summe 7 heißen trinitarische Zahlen.
5.
Nun ist nicht
nur die Summe 22 aus jeweils zwei
Komplementärzahlen durch 11 teilbar, sondern auch
die ersten beiden Zahlen 1 und 21 in dreistelliger Zusammensetzung: 121 = 11*11. Jede weitere dreistellige Zusammensetzung
erhöht sich um 99 = 9*11. In der folgenden
Tabelle werden die Zahlen durch 11 geteilt und von deren Ergebnissen die FW ermittelt:
|
Zahl |
11 |
121 |
220 |
319 |
418 |
517 |
|
616 |
|
715 |
814 |
913 |
1012 |
sm |
|
/11 |
1 |
11 |
20 |
29 |
38 |
47 |
146 |
56 |
202 |
65 |
74 |
83 |
92 |
516 |
|
FW |
1 |
11 |
9 |
29 |
21 |
47 |
118 |
13 |
131 |
18 |
39 |
83 |
27 |
298 |
|
sm |
|
|
|
|
|
|
264 |
|
333 |
|
|
|
|
814 |
|
814 = 74*11; 264:550 = 22*(12:25); 333:481 = 37*(9:11) |
||||||||||||||
Die Summe der durch 11
geteilten Zahlen und deren FW sind wiederum durch 11
teilbar. Setzt man die Einzelzahl 11 an den
Anfang, erhält man zwei Teilverhältnisse. Aufteilungen nach Punktzahlen und
Linienzahlen scheinen keine Verhältnisse zu ergeben.
Erstellt: Mai 2011