64
Zweistellige Komplementärzahlen
a) Überblick
b) 129 und 903
a) Überblick
1. Unter zweistelligen Komplementärzahlen sind Zahlenpaare zu verstehen, deren Zehner- und Einerstellen sich jeweils zu 10 ergänzen, z.B. 12 98 und 21 89. Unter ihnen befinden sich 4 Zahlen und ihre Umkehrungen, die in sich komplementär sind, da sich ihre Einzelziffern zu 10 ergänzen: 19-91, 28-82, 37-73, 46-64. Sie werden hier nicht berücksichtigt. Ihre Zahlensumme (ZS) ist 440, ihre Faktorensumme (FS) 240, zusammen 680 = 40*17. Die Summe der drei Primzahlen ist 129 = 3*43.
2. Zu den komplementären Paaren treten noch ihre Umkehrungen hinzu, sodaß es 16*4 Komplementärzahlen gibt. Die Summe von je vier Zahlen ist 20*11 = 220. Die Gesamtsumme beträgt 16*20*11 = 3520.
Die FS der 64 Komplementärzahlen beträgt 1750 = 25*70 = 7*250, die Zahlensumme + Faktorensumme 3520+1750 = 5270 = 10*17*31.
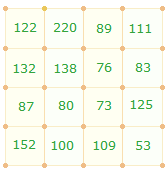
3. In der folgenden Tabelle werden in der obersten Zeile 16 Zahlen mit aufsteigenden Einerstellen aufgeführt, denen ebensoviele Komplementärzahlen entsprechen. In den darunter liegenden Zeilen stehen die jeweiligen Faktorenwerte (FW). Ab der 5. Zeile wiederholt sich dasselbe mit den Umkehrzahlen der ersten Zeile. Die 9. Zeile enthält die FS von je vier Zahlen. Die dazugehörigen ZS beträgt jeweils 220. Die violett gekennzeichneten Zahlen sind Primzahlen, von deren Summen in der letzten Spalte die FW ermittelt werden:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PZ |
FW |
|
|
ZW |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
23 |
24 |
25 |
26 |
27 |
34 |
35 |
36 |
45 |
380 |
53 |
53 |
|
|
2 |
FW |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
23 |
9 |
10 |
15 |
9 |
19 |
12 |
10 |
11 |
188 |
|
|
|
3 |
ZW |
98 |
97 |
96 |
95 |
94 |
93 |
92 |
87 |
86 |
85 |
84 |
83 |
76 |
75 |
74 |
65 |
1380 |
180 |
15 |
|
4 |
FW |
16 |
97 |
13 |
24 |
49 |
34 |
27 |
32 |
45 |
22 |
14 |
83 |
23 |
13 |
39 |
18 |
549 |
|
|
|
5 |
ZW |
21 |
31 |
41 |
51 |
61 |
71 |
81 |
32 |
42 |
52 |
62 |
72 |
43 |
53 |
63 |
54 |
830 |
300 |
17 |
|
6 |
FW |
10 |
31 |
41 |
20 |
61 |
71 |
12 |
10 |
12 |
17 |
33 |
12 |
43 |
53 |
13 |
11 |
450 |
|
|
|
7 |
ZW |
89 |
79 |
69 |
59 |
49 |
39 |
29 |
78 |
68 |
58 |
48 |
38 |
67 |
57 |
47 |
56 |
930 |
370 |
44 |
|
8 |
FW |
89 |
79 |
26 |
59 |
14 |
16 |
29 |
18 |
21 |
31 |
11 |
21 |
67 |
22 |
47 |
13 |
563 |
|
|
|
9 |
FS |
122 |
220 |
89 |
111 |
132 |
138 |
76 |
83 |
87 |
80 |
73 |
125 |
152 |
100 |
109 |
53 |
1750 |
903 |
129 |
|
1750
= 25*70; 903 = 21*43; 129 = 3*43 |
||||||||||||||||||||
|
380+1380 = 1760; 188+549 = 737 = 11*67; 737:1760 = 11*(67:160) = 11*227 = 2497 > FW 238 |
||||||||||||||||||||
|
830+930
= 1760; 450+563
= 1013;
1760+1013 = 2773 = 47*59 > 106; 238+106 = 344 = 8*43 |
||||||||||||||||||||
|
2*1760 = 3520; 3520+1750 = 5270 = 10*17*31 |
||||||||||||||||||||
Die ZS 380+830 = 1210 = 110*11 und 1380+930 = 2310 = 210*11 haben das Umkehrverhältnis 110*(11:21). 23 und 24 bilden die konzentrische Mitte der 16 Zahlen. Die Summe der Einzelziffern sind 30+80 = 110 und 130+80 = 210. Die Umkehrung der Einzelziffern führen zur Multiplikation mit 11, also 110*11 = 1210 und 210*11 = 2310. Die violetten Zahlen sind Primzahlen.
Die Differenz zwischen der FS 1750 und der ZS 3520 beträgt 1770. 175 und 177 sind die Konstitutivzahlen für ihre Summe 352.
4. Die Summen der FS in ungerader und gerader Reihenfolge ergeben das Verhältnis 840:910 = 70*(12:13):
|
sm |
122 |
|
89 |
|
132 |
|
76 |
|
87 |
|
73 |
|
152 |
|
109 |
|
840 |
|
sm |
|
220 |
|
111 |
|
138 |
|
83 |
|
80 |
|
125 |
|
100 |
|
53 |
910 |
Der ZS 220 für 4 zusammengehörige Komplementärzahlen entspricht die FS der Zahlen 1-25. Ein 5*5 Punkte Quadrat ist in 13 gerade und 12 ungerade Punkte einteilbar. Es enthält 16 Einzelquadrate, in die die FS der 16*4 Komplementärzahlen eingetragen werden können.
|
|
|
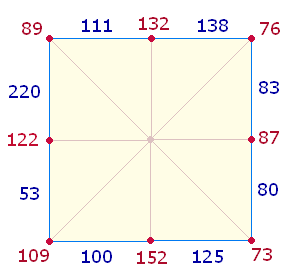
Die 16 FS können auch auf die 8 Punkte und 8 Linien des inneren Quadratrahmens gesetzt werden.
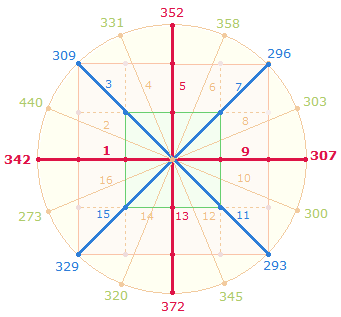
Der äußere Rahmen des 5*5 Punkte Quadrats besteht aus 16 Punkten. Um diesen kann ein Kreis mit 8 Achsenkreuzen errichtet werden. Er vermittelt die Vorstellung, daß das Ende der 16 Zahlen in den Anfang mündet. Tatsächlich ergibt die erste und letzte FS 53+122 = 175 ein Zehntel der Gesamtsumme 1750. Auf der folgenden Kreisfigur sind die 16 ZS+FS, zusammen 5270 eingetragen:
|
|
Eine Hälfte einschließlich der Horizontalachse umfaßt 9 Summen, die, ab Position 1 aufaddiert, 3038 = 2*31*7² ergeben. Es kommt so zur anderen Kreishälfte aus 7 Summen das Verhältnis 2*31*(49:36) = 62*85 = 5270 zustande. Ermittelt man rundum weitere 15 Male je 9 Summen, ist keine weitere durch 31 oder durch 17 teilbar.
Verfährt man
ebenso mit den FS,
ergeben 9 FS ab
Position 15 das
Verhältnis 1050:700 = 350*(3:2).
Hier ist die ZS 136 und FS 102 der Zahlen 1-16 einbezogen: Die Zahlen 15+16 und 1-7 haben die ZS 31+28 = 59 und die FS 16+27 =
43, zusammen 102.
Das ZS+FS-Verhältnis von 9:7
Positionen ist somit 34*(3:4). Für die
Positionen 1-9 ist das ZS+FS-Verhältnis
84:154 = 14*(6:11).
Die Positionen 1+15 = 16 und ihre FW 1+8 = 9 weisen auf das 5*5 Punkte Quadrat hin mit 16 Punkten des äußeren Rahmens und 9 Punkten des inneren Quadrats.
Verbindet man die Einzelziffern 1 und 9 der Horizontalachse zur zweistelligen Zahl 19, ergeben die ZW 13+5+19 die drei Achsenbuchstaben des SATOR-Quadrats: NET – Er webt.
5. Die FS 152 der Gruppe 34 ergibt, zur ZS 220 addiert, die einzige durch 31 teilbare ZS+FS: 220+152 = 372 = 21*31. Durch 17 ist keine ZS+FS einer einzelnen Gruppe teilbar.
Der logische Zusammenhang
zwischen 17 und 31
könnte u.a. so erklärbar sein:
·
Das Verhältnis von 10
Tetraktyspunkten zu 7 hexagonalen Punkten
gibt das Kreisflächenverhältnis 3:1 wieder.
Die FW von 10
und 7 sind 7+7 = 14; 17+14 = 31.
Gerechnet wurden also einmal die ZS und einmal
die ZS+FS
von 10 und 7. Vielleicht bezieht sich die zweite Addition
von 7
und 10 auch auf 7
Punkte und 10 Linien der DR beziehen.
·
Der ZW+FW
von 10 Tetraktyspunkten und 3*7 Elementen des Tetraktysrahmens: 10+7 = 17, 21+10 = 31. Die
Summe 48 ist als 2*24
symmetrische Elemente des Hexagons und seiner Erweiterung zum Tetraktysstern
interpretierbar.
· Die ZS+FS von 21
Elementen der DR ist 31, von 10 Maßeinheiten der DR 17.
Bezugspunkt für diese Interpretation ist das Wort HOMO
– Mensch:
|
|
H |
O |
sm |
M |
O |
sm |
GS |
|
ZW |
8 |
14 |
22 |
12 |
14 |
26 |
48 |
|
FW |
6 |
9 |
15 |
7 |
9 |
16 |
31 |
|
sm |
14 |
23 |
37 |
19 |
23 |
42 |
79 |
|
|
|
|
Dif.= 7 |
|
|
Dif.= 10 |
|
Die Differenz zwischen der FS 31 und der ZS 48 beträgt 17. Ein
DR-Kreuz kann aus zwei Rauten zu 2*11 = 22
Elementen und zwei Doppeldreiecken zu 2*13
= 26 Elementen zu einem
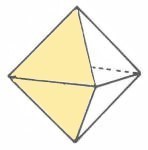
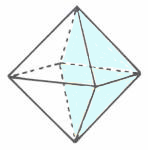
Oktaeder zusammengesetzt werden:
|
|
|
|
Die 72
Umkehrzahlen können wie eine DR oder als ein
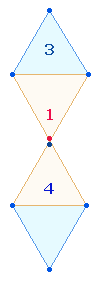
Oktaeder aus zwei entgegengesetzten Pyramiden verstanden werden. Weist man dem
Mittelpunkt des Tetraktyssterns die Zahl 1
zu, den übrigen Punkten die Zahl 2,
den Linien die Zahl 3 und den Flächen
die Zahl 4 zu, kommt für die 26 Elemente des Oktaeders die Summe 79, Komplementärzahl zu 31, zustande:
|
Okt. |
P |
L |
F |
|
|
|
1+5*2 |
12*3 |
8*4 |
|
|
|
11 |
36 |
32 |
79 |
|
FW |
11 |
10 |
10 |
31 |
Die ZS+FS der vier in sich komplementären Zahlen ist 440+240 = 40*(11:6) = 40*17 = 680. Das ZS+FS-Verhältnis der 64:8 Zahlen ist demnach 170*(31:4) = 170*35 = 50*7*17 = 5950. Die Einzelziffern der Verhältniszahlen ist auf die 7 Punkte der Doppelraute zu beziehen, die sich durch einen zweiten Mittelpunkt auf 8 erweitern:
|
|
1. Die ZS+FS von 9:7 Vierer-Gruppen nach obiger linearer Abfolge ergeben (1058+1980):(692+1540) = 3038:2232 = 2*31*(49:36), wie schon oben ermittelt.
Zur Ordnung gehören die addierbaren Positionen der Reihenfolge 1-16:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
FS |
122 |
220 |
89 |
111 |
132 |
138 |
76 |
83 |
87 |
80 |
73 |
125 |
152 |
100 |
109 |
53 |
Die Positionen 9+10 und 15+16
der zweiten Hälfte rahmen vier Innenglieder ein. 19
und 31 sind die ZW+FW
der Umkehrzahlen 12+7 = 19 und 21+10 = 31. Es
ergeben die FS 87+80
= 167; 109+53 = 162 zusammen 329; es
kommt hinzu die ZS 880,
zusammen 1209 = 39*31. Weiterhin läßt
sich hinzuaddieren 152+220 = 372 = 12*31.
Zusammen ergibt sich bei nunmehr 5
Positionen 51*31 = 3*17*31.
Es bleiben 7*17*31 zur Gesamt-ZS+FS 5270. Die
Positionen 1 und 3
ergeben 211+440
= 651 = 21*31. Durch
Umgruppierung erhält man 31*(12+21)
= 31*33 und das Verhältnis 31*(33:39) + 33*31
= 93*(11:13) = 72*31. Das Verhältnis von 7:9 Positionen ist nun 62*(36:49).
Die Verhältniszahlen 6² und 7² können sich auf ein 7*7
Punkte-Quadrat und auf 36 Einzelquadrate
beziehen, aber ebenso auf 49 Elemente des
Tetraktyssterns, der 24 Linien + 12 Dreiecksflächen enthält; 36 kann sich auch aus
zweimal 18 Rahmenelemente zweier Tetraktys
zusammensetzen.
Das Prinzip der Umkehrung wird durch die
dreidimensionale Figur des Oktaeders verwirklicht, der aus zwei
entgegengesetzten Pyramiden besteht. Die ermittelten Zahlenverhältnisse sind
auf die Gegebenheiten des Oktaeders beziehbar:
· Die Numerierungssumme 79
(s.o.) für die 26 Elemente des Oktaeders
kommt durch die ZS und FS der
4 Positionen der zweiten
Hälfte zustande:
|
ZW |
9 |
10 |
15 |
16 |
50 |
|
FW |
6 |
7 |
8 |
8 |
29
|
|
|
|
|
|
|
79 |
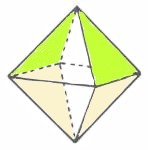
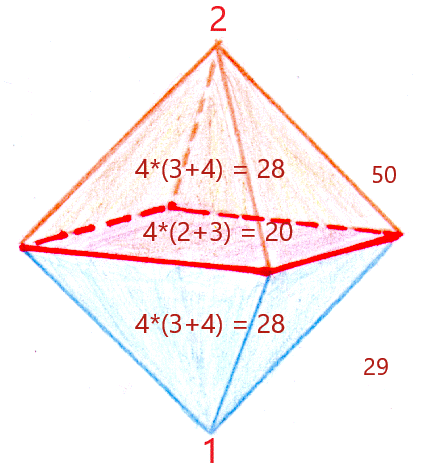
Die gemeinsame Mittelbasis der beiden
Pyramiden hat die Numerierungssumme 4*(3+2) = 20, die obere Pyramidenspitze hat
die Zahl 2, die untere, die aus dem Mittelpunkt des Tetraktyssterns hervorgeht,
die Zahl 1. Ohne Spitze ist die Numerierungssumme beide Male 4*(3+4) = 28. Mit
der Pyramidenspitze kommt für die obere 30
und die untere 29
zustande. Die Mittelbasis kann der einen oder der anderen Oktaederhälfte
zugewiesen werden. In vorliegendem Fall stellt die FS
29 die untere Hälfte des
Oktaeders ohne Mittelbasis dar, während die ZS die Mittelbasis und die obere
Pyramide umfaßt:
|
|
· Von seinen Außenelementen betrachtet besteht ein Oktaeder aus je 9 Elementen der beiden Pyramidenaufbauten und aus 8 Elementen der gemeinsamen Mittelbasis, zusammen
aus 26 Elementen. Für zwei selbständige
Pyramidenhälften sind 8 Elemente
hinzuzufügen, sie bestehen dann aus je 17,
zusammen 34 Elementen. Die Zahlen 26+8 ergeben sich aus den identischen ZW und FW der
Positionen 13 und 1+3.
1. Zuletzt wurde erkennbar, daß 12 und 21 die Grundzahlen aller zweistelligen Umkehrungen sind. Sie sind untrennbar mit den 10-er Einheiten des Dezimalsystem verbunden. Dies zeigt sich in den 17 Primzahlen der 64 Komplementärzahlen, deren Summe 903 = 21*43 beträgt. Sowohl die Addition der beiden Zahlen ergibt 64 als auch ihre Einzelziffern die Summe der Zahlen 1-4 = 10.
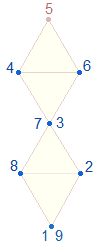
Die Zahl 10 verbindet die Tetraktys und die Doppelraute durch 10 Punkte und 10 Linien. Es wurde eingangs festgestellt, daß die vier in sich komplementären Zahlen die Primzahlen 19+37+73 = 129 = 3*43 enthalten. Tatsächlich werden die vier Umkehrpaarungen sichtbar, wenn man die 7 Punkte der DR schleifenförmig numeriert:
|
|
Aufgeteilt bedeutet 129 12 4*3 "Dachelemente" (Linie Punkt Linie) und 9 3*3 Längsachsenelemente. Auf diese Weise ergeben sich durch Teil- und Gesamtsumme die Umkehrzahlen 12 und 21.
Dasselbe gilt für den Tetraktysrahmen: Jede der drei Seiten besteht aus 4 Punkten + 3 Linien. 3*4 = 12 Punkte + 3*3 = 9 Linien ergibt 21.
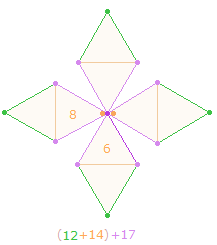
Nun ergeben die 4 FW der FS 53, 180, 300 und 370 wiederum 129, die FS der in sich komplementären Primzahlen 19+37+73, zusammen 903+129 = 1032 = 24*43. Es konkurrieren somit die Faktoren 21 und 24 der Summen 903 und 1032, sie sind auf die 21 Elemente der DR zu beziehen. Diese besteht aus 15 Rahmenelementen + 6 Binnenelementen. Der Rahmen seinerseits besteht aus je 9 Elementen zweier Zickzacklinien. Wenn man diese als eigenständig betrachtet, ergibt sich 9+9+6 = 24.
2. Zieht man die Primzahl-ZS 903 von der Gesamt-ZS 3520 ab, bleibt die Primzahl 2617. Die Addition 26+17 ergibt 43. Man erkennt in 26 die Zahl der Oktaederelemente und in 17 die Elemente einer Oktaederhälfte. Auch der Rahmen eines DR-Kreuzes besteht aus 17 hexagonalen Elementen. Die 25 hexagonalen Elemente vereinigen sich zu einer Pyramidenhälfte aus 17 Elementen.
Nun besteht ein DR-Kreuz bei einem Mittelpunkt aus 41 Elementen, einem Element weniger als 2*21. Um die Unterzahl auszugleichen, ist ein DR-Kreuz zu erstellen, dessen eine DR zwei Mittelpunkte enthält. Diese werden gewöhnlich zu den Rahmenelementen zugezählt. Um aber die Gleichheit von 17 hexagonalen Rahmenelementen mit 17 Oktaederelementen zu wahren, werden die zwei zusätzlichen Punkte zu den Binnenelementen gerechnet, wie aus folgender Grafik ersichtlich wird:
|
|
Entsprechend ihrer Zughörigkeit repräsentieren die 12, 14 und 17 Elemente 2, 3 und 1 Kreisflächeneinheiten. Den 6 und 8 Binnenelementen entsprechen 6 Ecken und 8 Flächen des Oktaeders.
3. Da die Primzahl-ZS 903 auch gleichzeitig die FS ist, ergibt 1750-903 = 847 = 7*11*11. Bemerkenswert ist die ZW/FW-Verrechnung:
|
|
ZS |
ZS |
FS |
FS |
sm |
FW |
|
|
903 |
2617 |
903 |
847 |
5270 |
55
|
|
FW |
53 |
2617 |
53 |
29 |
2752 |
55
|
|
sm |
|
|
|
|
|
110 |
|
2752 = 64*43 |
||||||
Der zweimalige FW 55 weist auf zwei gegenüberstehende und somit auch komplementäre, von 1-10 numerierte Tetraktys hin. Es scheint, als käme jeder der 64 Komplementärzahlen die Zahl 43 zu. 64 hat durch 26 Bezug zu den 26 Elementen des Oktaeders. 64 = 8*8 läßt sich so erklären: Die Radialelemente des Hexagons und einer DR-Zickzacklinie sind zweimal 3 und zweimal 5:
|
|
3:5 = 8 Radialelemente geben das trinitarische Kreisflächenverhältnis 1:3, also 4 Flächeneinheiten wieder. Der DR-Rahmen besteht aus zwei Zickzacklinien und somit aus 4*8 = 32 Radialelementen, die sich durch das DR-Kreuz auf 64 verdoppeln.
3:2 Radialelemente bedeuten 3 Flächeneinheiten.
Die Einzelziffern der Primzahl 43 bezeichnen also zwei Kreisflächenverhältnisse. Sie erhalten diese Bedeutung aber auch durch 4 und 3 Elemente, kombiniert durch 7 Punkte der DR und durch 7 Elemente einer Tetraktysseite :
|
|
|
Besonders bedeutsam erscheint die Gleichung der Tetraktysseite, da die ZS/FS 903 das Produkt 43*21 bildet.
1. 903 ist die Summe der 17 Primzahlen unter den 64 Komplementärzahlen. Sie ist sowohl auf die Tetraktys als auch auf die DR beziehbar. In der Produktaufteilung 3*301 kann man das Muster der 3+3+1 DR-Punkte erkennen. Der FW von 43*21 ist 43+10 = 53. Nun hat der Dichter OVID im 8. Buch der Metamorphosen in 53 Versen von 183-235 die Unglücksgeschichte von DAEDALUS und ICARUS erzählt. Auffallend sind 5 Einleitungs- und 5 Schlußverse.
2. OVID hat seine Verszahl offensichtlich nach den beiden Namen konzipiert:
|
|
D |
A |
E |
D |
A |
L |
U |
S |
sm |
|
ZW |
4 |
1 |
5 |
4 |
1 |
11 |
20 |
18 |
64 |
|
FW |
4 |
1 |
5 |
4 |
1 |
11 |
9 |
8 |
43 |
Mit der Zahl der 64 Komplementärzahlen stimmt die ZS von DAEDALUS überein. Die 8 Buchstaben haben den durchschnittlichen ZW 8. 21 ist die Differenz zwischen der FS 43 und der ZS 64.
Auch ICARUS weist eine Beziehung zu 903 und den drei Tetraktysseiten auf:
|
|
I |
C |
A |
R |
U |
S |
sm |
|
ZW |
9 |
3 |
1 |
17 |
20 |
18 |
68 |
|
FW |
6 |
3 |
1 |
17 |
9 |
8 |
44 |
Die drei Tetraktysseiten bestehen zusammengenommen aus 9 Punkten, jede einzelne Seite jedoch aus 4 Punkten. 3*4 Punkte ergeben 12, also 9+3. Die FW 6+3 stellen die 3*2 Linien der hexagonalen Erweiterung und die 3 hexagonalen Linien der drei Tetraktysseiten dar, sodaß der Teil zum Ganzen die Umkehrzahlen 12+21 hervorbringt.
Das R mit dem ZW 17 verbindet den Namen mit den 17 komplementären Primzahlen.
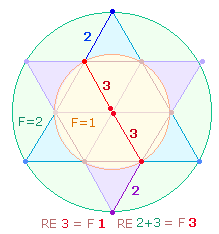
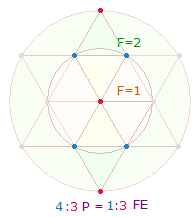
3. Die Buchstaben IC bekommen ihre ontologische Gültigkeit durch die Initialen von IESUS CHRISTUS. Die Umkehrzahlen 12+21 verbergen sich in den Initialen von MARIA IESUS. Sie sind sowohl auf 3*4 Punkte + 9 Linien der drei Tetraktysseiten als auch auf 4*3 Dachelemente + 9 Längsachsenelemente der DR beziehbar. Die FW der beiden Initialen sind 7+6 = 13. Der hexagonale Doppeldreieck der DR besteht aus 13 Elementen, sodaß 13:21 Elemente das Kreisflächenverhältnis 1:3 wiedergeben:
|
|
Die Einzelziffern der Verhältniszahlen 13:21 stellen in sich die beiden Kreisflächenverhältnisse dar. 1:3 und 2:1 lassen sich durch das FS-Verhältnis der zusammengesetzten Zahlen zu den Primzahlen der vier in sich komplementären Zahlen bilden:
|
|
19 |
28 |
37 |
46 |
130 |
91 |
82 |
73 |
64 |
310 |
440 |
|
PZ |
19 |
|
37 |
|
56 |
|
|
73 |
|
73 |
129 |
|
zsZ |
|
11 |
|
25 |
36 |
20 |
43 |
|
12 |
75 |
111 |
|
|
|
|
|
|
92 |
|
|
|
|
148 |
240 |
|
|
|
|
|
|
222 |
|
|
|
|
458 |
680 |
|
111:129 = 3*(37:43);
36:75 = 3*(12:25) |
|||||||||||
Die Einzelziffern der Primzahlen 37 und 43 sind, wie kurz zuvor grafisch dargestellt, auf eine Tetraktysseite beziehbar: 3:7 und 4:3 Elemente geben die Flächenverhältnisse 1:3 und 2:1 wieder. Das Verhältnis 25:12 bezeichnet 25 hexagonale Elemente und ihre Erweiterung zur Tetraktys durch 12 weitere Elemente.
Auch der zweimalige FW 55 (s.u.3.) ist in den ZS der beiden Namen verwirklicht, wenn ihre Buchstaben alternierend angeordnet werden:
|
M |
A |
R |
I |
A |
I |
E |
S |
U |
S |
sm |
|
12 |
|
17 |
|
1 |
|
5 |
|
20 |
|
55 |
|
|
1 |
|
9 |
|
9 |
|
18 |
|
18 |
55 |
|
|
|
|
|
|
|
|
|
|
|
110 |
II./III. Die Komplementärsumme 273
IV. Ordnung der Komplementärzahlen nach Primzahlen
V. 64 Komplementärzahlen in drei konzentrischen Quadraten
Erstellt: September/November 2014
Neu bearbeitet: November 2022