Punkte und Maßeinheiten
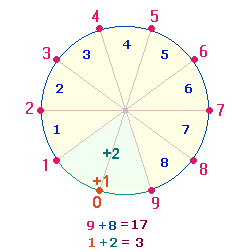
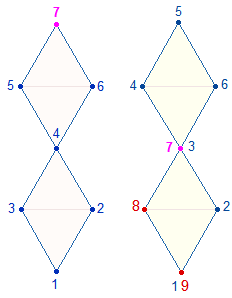
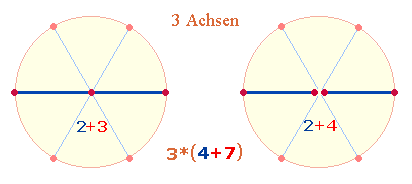
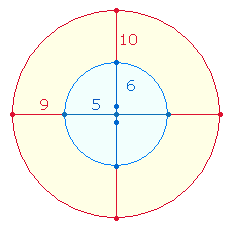
1. Maßeinheiten können nur gebildet werden, wenn sie punktartig voneinander abgegrenzt werden. Die Grundzahlen von 1-9 haben daher die Funktion, 8 Maßeinheiten zu begrenzen. Für die zwei übrigen Maßeinheiten, die zum Dezimalsystem gehören, ist ein nicht-zählbarer Nullpunkt erforderlich. Die folgende Grafik enthält in Kreisanordnung 10 Punkte und 10 Maßeineiten:
|
|
2. Nullpunkt + zwei Maßeinheiten gehören nicht zu den Grundzahlen. Sie bilden eine eigene Sinnkategorie.
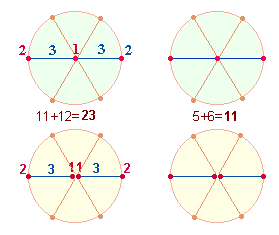
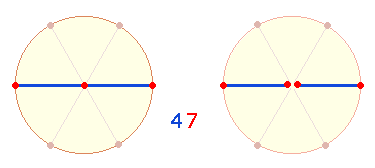
Die angezeigte Numerierung nach Punkten und Maßeinheiten ermöglicht eine Reihe von acht dreistelligen Zahlen und ihren Umkehrungen. Die Ergebnisse sind sowohl nach den Zahlensummen (ZS) als insbesondere den Faktorensummen (FS) zu untersuchen:
|
Zahl |
112 |
223 |
334 |
445 |
556 |
667 |
778 |
889 |
4004 |
|
Uk |
211 |
322 |
433 |
544 |
655 |
766 |
877 |
988 |
4796 |
|
FW |
15 |
223 |
169 |
94 |
143 |
52 |
391 |
134 |
1221 |
|
FW/Uk |
211 |
32 |
433 |
27 |
136 |
385 |
877 |
36 |
2137 |
|
|
226 |
255 |
602 |
121 |
279 |
437 |
1268 |
170 |
3358 |
|
4004:4796 = 4*(1001:1199) =
4*11*(91:109) >FW 30+129 = 159 |
|||||||||
Die Numerierungssumme der Punkte beträgt 36+44 = 80, die der Maßeinheiten 36, das Verhältnis 80:36 = 4*(20:9). Die Klammerzahlen lassen sich zusammensetzen aus 5*4 und 5+4.
Konzentrisch ergeben je zwei Zahlen eine durch 11 teilbare Summe. Auffällig sind die Umkehrungen 91 und 109. Die Zahlen 10 und 9 sind nicht auf Punkte und Maßeinheiten zu beziehen, sondern auf gerade und ungerade Zahlen.
Die Primzahl 109 ist auch in der Summe der vier farbig hervorgehobenen Zahlen enthalten: 1744 = 16*109; der Durchschnittswert ist 4*109 = 436. Die Summe der übrigen 12 Zahlen ist 1614 (s.unten).
Das Verhältnis 1:3 ist zweifach vertreten: erstens, eine aufsteigende, drei absteigende Primzahlen, zweitens, 4:12 Zahlen ist 4*(1:3).
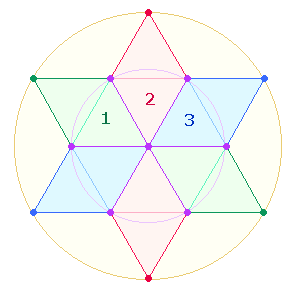
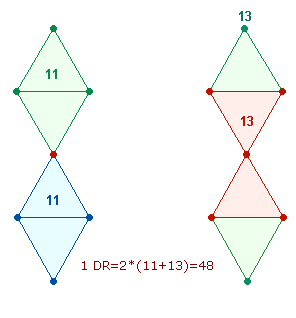
3. Wie in den meisten Fällen sind erschließen sich die Ergebnisse erst durch das geometrische Modell des Tetraktyssterns, der aus zwei Tetraktys und drei Doppelrauten (DR) besteht:
|
|
Tetraktys und DR besitzen einige Gemeinsamkeiten: Die DR besteht aus 21 = 3*7 Elementen, die Tetraktys aus 37 Elementen, wobei der Tetraktysrahmen sich aus 3*7 = 21 Elementen zusammensetzt. Daher sind stets beide Figuren zu berücksichtigen.
Die in der Kreisanordnung erkennbare Aufteilung von 8+2 Maßeinheiten zeigt sich in der DR als 8 Rahmenlinien und 2 Querlinien.
Die Zickzacklinie einer DR besteht aus 9 Durchmesserelementen und 2*5 = 10 Radialelementen. Es handelt sich um einen zu zählenden Doppelaspekt ebenso wie die 5 DM-Elemente und 6 Radialelemente der Kreisachse. Eine weitere Kombination von 10+9 stellen die 10 Punkte und 9 Dreiecke der Tetraktys dar.
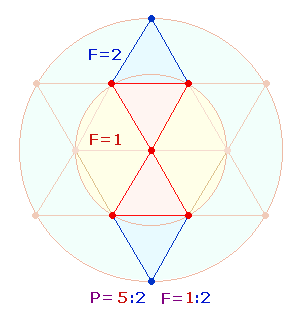
4. Charakteristisch für die DR sind 5 Punkte des hexagonalen Bereichs und je 1 Punkt für den Erweiterungsbereich. Hierdurch wird die Primzahl 151 zu einer besonderen Symbolzahl:
|
|
5:2 Punkte bedeuten das Kreisflächenverhältnis 1:2, was sich als Parallele zu Nullpunkt + 2 Maßeinheiten anbietet.
Die Summen 1001 = 7*11*13 und 1199 = 11*109 haben den FW 31+120 = 151.
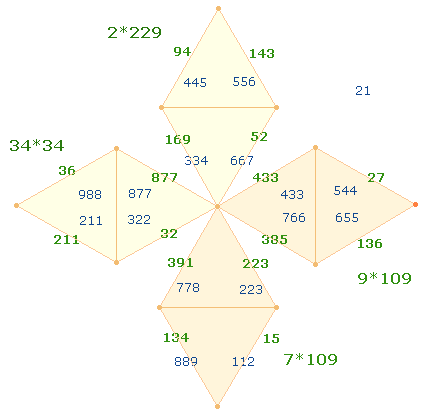
5. Die DR haben nicht nur für sich allein Bedeutung, sondern haben die Funktion, zu je zweien ein Achsenkreuz zu bilden und sich zu einem Oktaeder zusammenzufügen. Die 26 Oberflächenelemente des Oktaeders setzen sich zusammen aus den Konstitutivzahlen 14+12, d.h. aus 6 Ecken + 8 Flächen und 12 Kanten. Die 8 Zahlen und ihre Umkehrungen lassen sich auf den Rahmenlinien schleifenförmig eintragen. Von besonderer Bedeutung sind die FW:
|
|
Die FS der unteren und rechten Raute 16*109 ist dieselbe wie die Summe der vier Primzahlen. 9 und 7 sind die Konstitutivzahlen der Zahl 16 und entsprechen komplementär den Zahlen 1 und 3. Die Erklärung ist folgende: Die Quadratzahl 16 entsteht aus der Summe der Zahlen 1-3 = 6 und 1-4 = 10. Aus den Endzahlen 3+4 = 7 bestehen das Hexagon und die DR. Zählt man für jede hexagonale Achse 3 Punkte, ist die Summe 9. Ebenso erhält man 9 Zahlen, wenn man die Punkte der DR schleifenförmig anordnet:
|
|
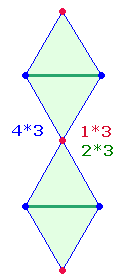
6. Die Summe der 8 aufsteigenden Zahlen 1221 gibt das Verhältnis des Teils zum Ganzen in der Tetraktys und in der DR wieder:
|
|
|
Im ersten Fall ergeben 3*4 Punkte der drei Tetraktysseiten 12 und zusammen mit 9 Linien 21, im zweiten Fall werden 4*3 "Dachelemente" durch 9 vertikale Elemente zu 21 ergänzt.
Die Primzahl 2137, die Summe der absteigenden FW, verbindet die 21 Elemente der Doppelraute mit den 37 Elementen der Tetraktys.
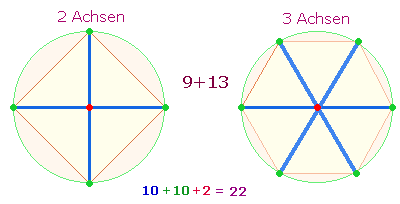
7. Die ZS+FS aller Zahlen beträgt 8800+3358 = 12158 = 2*6079. Die Einzelziffern der Primzahl 6079 egeben 22, ebenso die Aufteilung 13+9, wenn man die Addition 60+79 = 139 ausführt. Hintergrund hierfür sind 10 Maßeinheiten, die sich aus einem zweiachsigen und einem dreiachsigen Achsenkreuz ergeben:
|
|
Die zusätzliche Achse des Hexagons fügt zu 9 Elementen 2+2 hinzu. Dies ist erkennbar in der FS 458 = 2*229 der oberen Raute, ebenso in der Zahl 556 = 4*139.
Der FW der ZS+FS 12158 ist 6081 = 3*2027. Die Primzahl 2027 ist ebenfalls auf die beiden vorstehenden Achsenmodelle beziehbar, wenn man die Achsenpunkte doppelt zählt, einmal mit jeweils einem Mittelpunkt und einmal mit einem Mittelpunkt für jede Achse. Auf diese Weise ergibt sich (10+2)+(10+5) = 27. Parallel dazu sind auch die 10 Maßeinheiten zu 20 zu verdoppeln.
Durch Aufteilung des FW in 60+81 erhält man 141 = 3*47. Die Einzelziffern 4 und 7 kommen ebenfalls durch eine Doppelrechnung einer hexagonalen Kreisachse zustande, indem einmal ein Mittelpunkt für 5 Durchmesserelemente und einmal zwei Mittelpunkte für 6 Radialelemente gezählt werden:
|
|
8. In einem vollkommenen System enthält stets der Teil auch das Ganze. Dies läßt sich erkennen, wenn man jede zweite FS addiert:
|
226 |
|
602 |
|
279 |
|
1268 |
|
2375 |
|
|
255 |
|
121 |
|
437 |
|
170 |
983 |
Die Primzahl 983 enthält 9 Punkte und 8 Maßeinheiten sowie die 3 Nullelemente. Dasselbe ist der Fall bei der FS 1268 = 4*317.
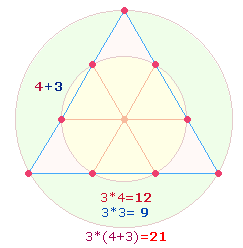
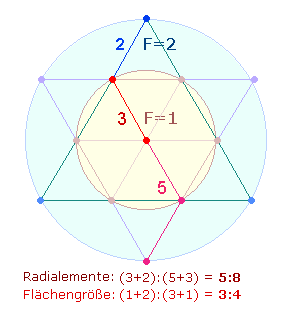
9. Das Dezimalsystem besitzt eine solche innere Sinndichte, daß Zahlen auf einer unteren Ebene sich auf einer höheren Ebene wiederholen. Ein Beispiel hierfür sind die 7 Punkte des Hexagons und der Doppelraute. Sie wiederholen sich in zwei Kreisflächenverhältnissen des Hexagramms, in der folgenden Grafik an den Radialelementen dargestellt:
|
|
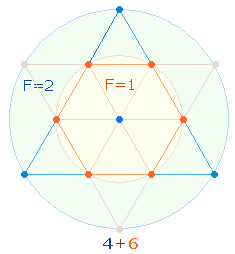
Das erste Flächenverhältnis bezieht sich auf den hexagonalen Kreis und den erweiterten Kreisring, es beträgt 1:2, das zweite setzt den inneren Kreis in Beziehung zum ganzen äußeren Kreis, das Verhältnis ist nun 1:3. Die entsprechenden Radialelemente sind 3+2 = 5 und 3+5 = 8.
Auch die Zahl 58 enthält die 7 Flächeneinheiten: Auf der Skala von 1-9 entsprechen den Flächeneinheiten 1+2 und 1+3 die komplementären Zahlen 9+8 = 17 und 9+7 = 16, zusammen 33. Die FW der vier Einzelziffern betragen 6+6 = 12 und 6+7 = 13, zusammen 25. Auf diese Weise beträgt die ZS+FS 33+25 = 58.
Aus den Ergebnissen 33 und 58 setzt sich auch die FS 3358 zusammen. Ihre Faktoren sind 2*23*73. Die Einzelziffern des FW 98 geben wiederum die 9 Punkte und 8 Maßeinheiten wieder. Die Einzelziffern des Produkts 46*73 sind auf die 10 Punkte der Tetraktys beziehbar:
|
|
|
7+3 und 4+6 Punkte geben die Flächenverhältnisse 1:2 und 3:1 wieder, zweistellig addiert 43. Punkte und Flächeneinheiten ergeben addiert 15+12 = 27.
Durch Aufteilung 33+58 erhält man 91 = 7*13. Neben der Gleichsetzung von 7 Flächeneinheiten und 13 Radialelementen bedeuten 7 hexagonale zu 13 Punkte des Hexagramms das Kreisflächenverhältnis 1:3.
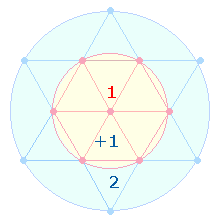
10. Die Einzelziffern der Ausgangszahl 112 sind als Kreisflächenverhältnis 1:3 verstehbar:
|
|
Die Hinzufügung des FW 15 ergibt die Primzahl 127. Sie ist die FS der Zahlen 1-18. Die Konstitutivzahlen für 18 sind 10+8. Auf der Skala der Zahlen von 1-10 sind sie Komplementärzahlen zu 1+3. Es ist an 10 und 8 Maßeinheiten zu denken, die durch 11+9 Punkte begrenzt werden. Auf gematrischer Ebene bedeutet 20+18 die Maskulinendung -US.
11. Weitere Sinnzusammenhänge zeigen sich in den ZS+FS der aufsteigenden und absteigenden Zahlen:
|
|
ZS |
FS |
sm |
ZS |
FS |
sm |
GS |
|
|
4004 |
1221 |
5225 |
4796 |
2137 |
6933 |
12158 |
|
FW |
35 |
51 |
86 |
124 |
2137 |
2261 |
2347 |
|
|
|
|
5311 |
|
|
9194 |
14505 |
Die
Palindromzahl 1221 setzt sich fort in der
Summe 5225 = 25*11*19. Sie enthält in Umkehrung und
zweistelliger Form die zwei Kreisflächenverhältnisse 21+31 und 12+13. Die Faktoren 11 und 19
setzen sich zusammen aus dem Doppelaspekt von 5
und 9 Durchmesserelementen (horizontal) und 6 und 10
Radialelementen (vertikal) des Hexagramms, darstellbar durch eine
Achsenkreuz:
|
|
11:19 Elemente geben das Flächenverhältnis 1:3 der beiden Tetraktyskreise wieder. Die getrennte Zählung von Radialelementen und DM-Elementen ergibt 16 und 14, ihre Zusammensetzung 1614 ist die FS von 12 Zahlen außer den 4 Primzahlen (s.o.).
12. Derselbe Doppelaspekt in der Summe 6933 bezieht sich auf die drei Hexagonachsen, also 3*23 und 3*11. Es verbindet sich hier die numerierte und unnumerierte Zählweise:
|
|
Die Summe 6933 ist deshalb so bedeutsam, weil sie den 8 Buchstaben des SATOR-Quadrats zugrundeliegt, nur in umgekehrter Reihenfolge:
|
P |
E |
N |
S |
A |
T |
O |
R |
|
15 |
5 |
13 |
18 |
1 |
19 |
14 |
17 |
|
33 |
69 |
||||||
13. Von gematrischer Bedeutung ist die prime FS 2347. 23 ist die FS und 47 die ZS des Wortes IUS – das Recht bzw. VIS – die Macht. Analog zum Wort VESTA, in dem ES – Du bist an 2. und 3. Stelle steht, die ZS 23 hat und verstanden werden kann als Du bist das TAU, ist die religiöse Anrede Du bist das Recht, Du bist die Macht möglich. Als reine ZS mit ebenfalls 2. und 3. Position hat sich ES IUS/VIS im Namen IESUS erfüllt.
14. Die Faktoren der Gesamtsumme 14505 sind 3*5*967 = FW 975 = 75*13 = 13+13 = 26. In der Zahl 967 begegnen wiederum die zwei Achsenkreuze aus 9 und 13 Elementen. Tatsächlich entsteht der Oktaeder aus einer Verbindung von Dreiachsigkeit und Zweiachsigkeit. Der FW 26 weist auf die 26 Elemente des Oktaeders hin.
15. Man unterscheidet zwischen externer und interner Differenz von FS und ZS. Bei der externen Differenz werden beide Werte gezählt, bei der internen nur die Zusammensetzung zwischen FS und dem Differenzbetrag zur ZS. Im Fall des Wortes IUS ist dieser Doppelaspekt 23+47 und 23+24, zusammen 46+71 = 117 = 9*13. 23 und 24 sind Zusammensetzungen der Einzelziffern 2, die jeweils zwei radiale Maßeinheiten darstellen, und einmal 3 DM-Punkte und einmal 4 Radialpunkte:
|
|
Es bedeutet wiederum eine Wiederholung auf höherer Ebene, daß die ZS+FS der Zahlen 1-23 und 1-24 durch 47 teilbar ist: 276+300 = 576; 201+210 = 411; 576+411 = 987 = 21*47.
Die ZW/FW-Verrechnung der ZS+FS der auf- und absteigenden Zahlen führt auch zur Summe 987:
|
|
|
|
sm |
FW |
sm |
|
ZS+FS |
5225 |
6933 |
12158 |
6081 |
|
|
FW |
40 |
2314 |
2354 |
120 |
|
|
sm |
|
|
14512 |
6201 |
|
|
FW |
|
|
915 |
72 |
987 |
|
2354 = 22*107; 14512
= 16*907 |
|||||
|
6201 = 9*13*53 |
|||||
Die ZW/FW-Verrechnung der ZS+FS 12158 und 2347 führt zu einem Bezug der Oktaederbildeung:
|
|
ZS |
FS |
sm |
FW |
sm |
FW |
|
|
12158 |
2347 |
14505 |
975 |
|
|
|
FW |
6081 |
2347 |
8428 |
61 |
|
|
|
sm |
|
17*19*71 |
22933 |
1036 |
23969 |
2190 |
|
FW |
|
|
107 |
48 |
155 |
36 |
|
|
|
|
|
|
|
2226 |
Ein Oktaeder setzt sich zusammen aus 2*11 Elementen zweier Rauten und 2*13 Elementen zweier Doppeldreiecke. Die beiden folgenden DR müssen als Achsenkreuz gesehen werden:
|
|
Erstellt: August 2015