Grundlagen der Quadratbildung
Weitere Modellelemente und ZahlenbedeutungenI. Das Problem des Radius und der
Begrenzungspunkte II. Zahlendarstellung des Mittelpunktes
und der übrigen Elemente a)
Quersummen dreistelliger Zahlen b) Die Zahlen 114, 214, 124, 224 und ihre Umkehrungen Die doppelte Quadratbildung aus einem
Achsenkreuz ist unter Allgemeines über Achsenkreuze behandelt worden. Das nachstehende
geometrische Modell dient auch weiterhin als Ausgangspunkt weiterführender
Untersuchungen: I. Das Problem des
Radius und der Begrenzungspunkte 1. In der
Betrachtung von Punkten und Linien gibt es keine eindeutige Dominanz. Ihre Beziehung zueinander
ist vielfältig. Wenn man vom Radius spricht, meint man den gleichmäßigen
Abstand der Kreislinie von ihrem Mittelpunkt. Die meßbare Radiallinie ist in
der Kreisbildung impliziert. Sie wird explizit, wenn man den Mittelpunkt mit
der Kreislinie verbindet. Eine zweite Radiallinien kommt hinzu, wenn man die
erste in symmetrischer Gegenrichtung verlängert, bis sie die Kreislinie
wiederum schneidet. Man kann nun eine einzelne Radiallinie und beide zusammen als Einheit
betrachten. Auf diese Weise erhält man zweimal einen Mittelpunkt für die
Radiallinien und einmal für den Durchmesser. Ein Radius mit sichtbarer
Verbindungslinie besteht daher aus 3 Elementen,
der Linie und zwei Begrenzungspunkten, der Durchmesser aus dem Mittelpunkt
und je zwei symmetrischen Elementen aus Punkt und Linie. Der Durchmesser hat
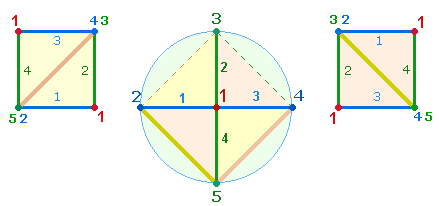
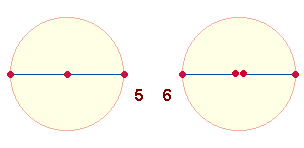
somit das Modellcharakter für ungerade, die beiden Radien für gerade Zahlen: 5 und 3+3. Die beiden
Modelle sind als komplementär in zwei Kreisen vorzustellen:
2. Dieses
Vorstellungsmodell läßt sich in einem Achsenkreuz darstellen: Eine Achse
besteht aus ungeraden Durchmesserelementen, die zweite aus geraden
Radialelementen. Wenn man dieses Modell als komplementär zu einem Achsenkreuz
mit einem einzigen Mittelpunkt ansieht, beträgt die Summe der Elemente 4-mal
die Zahl der Elemente einer Achse:
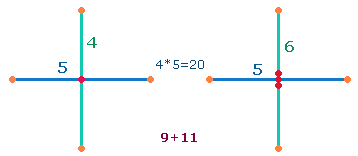
3. Wenn man Komplementarität
auch der Quadratbildung aus einem Achsenkreuz zuerkennt, kommen zum einen Mittelpunkt des Achsenkreuzes vier extrapolierte radiale Mittelpunkte in den beiden
Quadraten hinzu. Achsenkreuz und 2 Quadrate bilden eine Einheit von 3
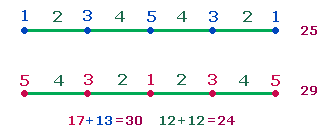
geometrischen Figuren aus 5+6+6 = 17 Punktepositionen + 3*4 = 12 Linien = insgesamt 29 Elementen; durch Zusammenfall von 2*2 Achsenarmpunkten ist die reale Zahl der Punkte 13, sodaß die Gesamtzahl der Elemente 25 beträgt. Numeriert man eine Achse aus 9 Elementen konzentrisch vom Mittelpunkt weg und zum Mittelpunkt hin, ist
die Summe einmal 29 und einmal 25:
Den 17 Punktepositionen und 13 Punkten entsprechen die Numerierungssummen
der Punkte auf den beiden Achsen, die Zahl der Linien in beiden Zählungen
stimmt mit der Numerierungssumme der Linien überein. Die Verhältnis 30:24 = 6*(5:4) weist auf die 9 Elemente des Basisachsenkreuzes zurück. Wie steht es
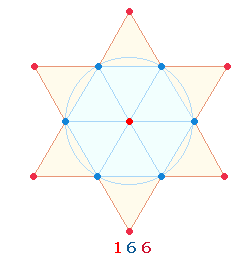
mit den Radialmittelpunkten der 3 Achsen des
Hexagons? Auch hier kann eine Extrapolation angenommen werden. Sie entsteht
durch die Erweiterung der Segmentlinien zum Tetraktysstern. Dem einen Mittelpunkt des Hexagons stehen 6
Radialmittelpunkte der geometrischen Erweiterung gegenüber:
II. Zahlendarstellung
des Mittelpunktes und der übrigen Elemente a) Quersummen
dreistelliger Zahlen 1. Der Mittelpunkt
regulärer geometrischer Figuren steht der geraden Zahl symmetrischer Elemente
stets eigenständig als ungerade Zahl gegenüber. Faßt man also die
Numerierungssummen des Mittelpunktes und der übrigen Elemente zu
dreistelligen Zahlen zusammen, ergeben sich für Basisachsenkreuz und Quadrat
für die Punkte die Zahlen 114 und 214 und für Punkte + Linien die Zahlen 124 und 224. Die Quersummen der ersten beiden
Zahlen sind 6 und 7, der
letzten beiden 7 und 8. Man kann
sie zu zweistelligen Zahlen 67 und 78 zusammenfassen. 2. Die Faktorenwerte
(FW) der beiden Zahlen und ihre
Umkehrungen führen zu folgenden Ergebnissen:
Die Verhältniszahlen 9 und 5 geben einen gegenseitigen Verweis auf die 5 Punkte und
9 Gesamtelemente des AK2. Das ganze Verhältnis 10*(9:5) jedoch bezieht sich auf die
Situation des Tetraktyssterns: Eine Hexagonachse aus 5 Elementen wird zu 9 Elementen erweitert, die durch
einen zusätzlichen Mittelpunkt zu 2*5 = 10
Radialelementen werden. Schlägt man, parallel zum Hexagon, um dessen
Erweiterung einen Kreis, beträgt seine Gesamtfläche das Dreifache des
Hexagonkreises. Überträgt man die drei Zahlen des Verhältnisses auf die
Flächengröße, erhält man die Werte 3+(3+1). Wenn man
die erste Zahl in 1+2 für die Hexagonfläche und den
äußeren Kreisring aufteilt und den Klammerausdruck addiert, kommt man
wiederum zur 3-stelligen Zahl 124. Das Verhältnis 17:11 bezieht sich auf die Numerierungssumme der Dreiecksseite der Tetraktys und der
Hexagonachse. Die Umkehrsummen der zwei Zahlenpaare sind 143+165 = 308. Das
Verhältnis der Faktorensumme (FS) zur
Zahlensumme (ZS) ist 140:308 = 28*(5:11), das Differenzverhältnis 28*(5:6). |
||||||||||||||||||||||||||||||||||
Erstellt:April 2008