zurück

Die drei göttlichen Personen in Hexagon und Tetraktysstern

I. Einleitung

II. 3 Doppelkreise im Hexagon

a) Kreisbogennumerierung

b) Axialnumerierung

III. 3 Doppelrauten im Tetraktysstern

ZW/FW-Verrechnung

I. Einleitung

1. In diesem Beitrag sollen die drei göttlichen Personen jeweils 3 geometrischen Figuren des Hexagon und des Tetraktyssterns zugeordnet werden. Dazu werden jeweils die Punkte numeriert.

Den folgenden Überlegungen geht der vorbereitende Beitrag Die trinitarische Gleichung 1+2=3 voraus.

2. Zur Bestimmung der 3 göttlichen Personen werden zu den Zahlensummen auch noch die Faktorensummen hinzugenommen. Auch die ZW/FW-Verrechnung wird am Ende eine wichtige Rolle spielen.

3. Ich werde die auftretenden Zahlen deuten, so gut ich vermag, und soweit sie dem Gesamtplan des Themas dienlich sind.

II. 3 Doppeldreiecke im Hexagon

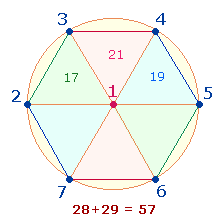
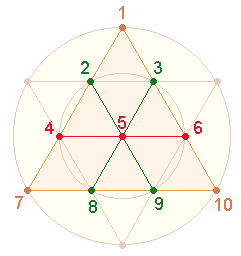
Im Hexagon kann man 3 sanduhrförmige Doppeldreiecke erkennen. Sie sind als Versinnbildlichung der drei göttlichen Personen anzusehen.

a) Die Kreisbogennumerierung

1. Die Numerierung der 7 Punkte beginnt im Mittelpunkt, wendet sich nach links und folgt im Uhrzeigersinn den Kreislinienpunkten:

2. Die Summe der Zahlen 1-7 ist 28, die Zahl 1 wird dreimal, die übrigen zweimal gezählt.

3. Die Gesamtsumme ist 57 = 3*19, das Dreifache der 5 Zahlen des rechten Doppeldreiecks. Daher gilt hier die Gleichung 1+2=3 in etwa folgender Form:

p1 = a

p2+p3 = 2a

zw = p2+p3

p1+zw = 3a

p bedeutet Person, zw die Zahl 2 für die 2. und 3. Person.

4. Das rechte Doppeldreieck mit der Summe 19 kommt also der ersten göttlichen Person zu. Die Zahl 19 setzt sich zusammen aus einer Doppelzählung von 2*5 Radial- und 9 Durchmesserelementen des Doppelkreises des Tetraktyssterns zusammen.

Die 1. Person ist also für das trinitarische Grundkonzept zuständig, dessen Endform der Tetraktysstern ist.

5. Die vertikale X-Form der Mittelfigur weist auf eine Vermittlungsfunktion hin. Die Zahl 21 besteht aus 3*7 und weist somit auf die 3. göttliche Person hin.

Die 3. Person ist die Vollendung des Konzeptes des dreieinen Gottes, sein Garant und gleichsam sein Sachwalter.

Die 3. Person führt auch das Dezimalsystem zu seiner vollendeten Form: Die Zahl 21 setzt sich aus 11 Begrenzungspunkten und 10 Maßeinheiten zusammen.

6. Die Zahl 17 besteht aus 9 Begrenzungspunkten und 8 Maßeinheiten. Die Zahlen 1-9 sind die Grundzahlen von Zeit, Raum und allem Geschöpflichen. Die 2. göttliche Person ist das vollkommene Abbild der 1. Person, "das Ebenbild des unsichtbaren Gottes" (Kol 1,15); "Ohne das Wort (logos) wurde nichts, was geworden ist." (Joh 1,3) Sie wurde im Menschen Jesus selbst irdisches Geschöpf und nach seinem Erlösungswerk Haupt der neuen Schöpfung: "Mir ist alle Macht gegeben im Himmel und auf der Erde." (Mt 28,18)

7. Die Zahlen 9+8, 10+9, 11+10 bezeichnen nicht nur Punkte und Maßeinheiten, sondern sind auch Komplementärzahlen zu den trinitarischen Anfangszahlen 1+2, die jedoch auch die Funktion von 2 Punkten und 1 Maßeinheit (Linie) übernehmen können, sodaß in der Linie die 3. Person die Zahl 1 einnimmt.

Eine Trennung nach Punkten und Maßeinheiten ergibt für jede Person:

	P	L
1. Person	12	10	22
2. Person	11	9	20
3. Person	13	11	24
	36	30	66

b) Die Achsennumerierung

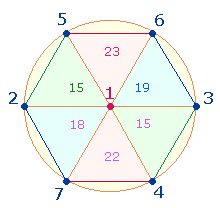
1. Bei dieser Numerierung werden jeweils 2 Kreislinienpunkte einer Achse numeriert, bevor im Uhrzeigersinn zur nächsten fortgeschritten wird:

2. Die Grafik enthält neben den Zahlenwerten (ZW) auch die Faktorenwerte (FW). Letztere weichen nur bei der Zahl 6 (FW=5) vom Zahlenwert ab. Ihre Summe ist um 2 Zähler niedriger als die Zahlensumme: 57+55 = 112.

3. Bei dieser Numerierung bleibt die Summe 19 für das rechte Doppeldreieck erhalten, die anderen beiden haben abweichende Ergebnisse.

Die ZS+FS der 1. Person ist 37, die der beiden anderen 75. Die Zahl 75 setzt sich zusammen aus 38+37. Wenn die 2. und 1. Person dieselbe Zahl haben, lassen sich die drei Werte als Kreis und als Strecke darstellen: Anfang und Ende des Kreises fallen zusammen. In der Streckendarstellung wird der 3. Punkt sichtbar. Der 2. Punkt als Mittelglied kommt wiederum der 3. Person zu:

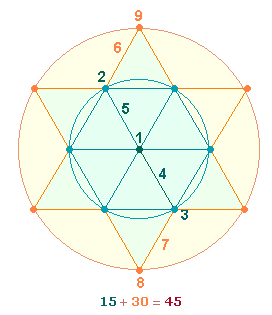
4. Die ZS+FS der 2. und 3. Person sind 30 und 45. Die beiden Summen bilden das Verhältnis 15*(2:3) und kennzeichnen so die beiden Personen.

Die Zahl 45 ist die Summe der Zahlen 1-9, die Zahl 30 die Summe der Zahlen 6-9. Auf die 9 DM-Elemente des Tetraktyssterns bezogen bedeutet 45 demnach die Flächengröße 3 und die Zahl 30 als Summe der Zahlen 6-9 die Flächengröße 2 des Kreisrings. Die folgende Grafik zeigt eine der Numerierungsmöglichkeiten der 5 DM-Elemente des inneren und den 2+2 DM-Elementen des äußeren Kreisrings:

III. 3 Doppelrauten im Tetraktysstern

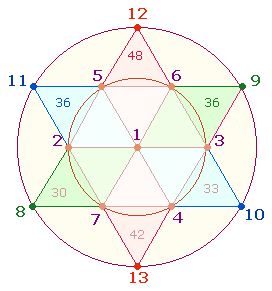
1. Die 3 Doppeldreiecke werden zu Doppelrauten im Tetraktysstern. Hinsichtlich der Bestimmung der drei göttlichen Personen erweist sich die axial fortschreitende Numerierung besonders aussagefähig. Die Zahlen 8-13 schließen sich unmittelbar an die Hexagonnumerierung an:

2. Die folgende Tabelle zeigt die ZS+FS der 3 DR:

DR	ZS	FS	Sm
Links	36	33	69
Mitte	48	42	90
Rechts	36	30	66
	120	105	225

Neu zu den ZS+FS 57+55 = 112 der 3 Doppeldreiecke kommen 63+50 = 113. Auffällig sind die beiden angrenzenden Summen als Konstitutiven für die Zahl 225, die in ihren Einzelziffern die 4 DM-Elemente des äußeren Kreisrings und die 5 DM-Elemente des inneren Kreises zeigt.

Das Quadratzahlprodukt 15*15 = 3*5*3*5 weist zunächst auf die quadratische Eigenschaft des Kreises hin. Einen zweiten Bezug bilden die doppelt zu rechnenden Radialelemente, 3 für den inneren, 5 für den inneren + äußeren Kreis. Weiterhin besteht ein DR-Rahmen aus 15 Elementen (7P+8L). Aus 2 zusammengefügten Doppelrauten besteht ein Oktaeder.

3. Für die linke und rechte DR errechnet sich die identische ZS 36. Es gilt zunächst weiterhin die Vermutung, daß die rechte DR der 1. Person, die linke DR der 2. Person zuzuordnen ist.

Das Verhältnis der 3 ZS ist 3*4*(3:4:3). Die Verhältniszahlen erinnern an den Tetraktysrahmen mit 3*(4P+3L). Sie setzen aber insbesondere die oben bereits festgestellte Einteilung der Hexagonpunkte in 3+4 in den 3 Eckpunkten der Tetraktys fort:

Die Summen der 3 Zahlengruppen sind 15+22+18. Die Summe der ersten und dritten Gruppe verhält sich zur Summe der zweiten Gruppe 33:22 = 11*(3:2); die Quersummen der beiden Summen 6+4 geben die Gruppeneinteilung der 10 Zahlen in (3+3)+4 wieder.

Wenn die 7 Punkte des Hexagon für die Flächengröße 1 und die 10 Punkte der Tetraktys für die Flächengröße 3 steht, bedeutet das ermittelte Verhältnis von 3*4*(3:4:3) das trinitarische Flächenverhältnis 1:3.

Die Zahlen 6+4 entsprechen den Punkten und Linien der 10 Radialelemente des Tetraktyssterns. Die Summen sind – wegen ihrer komplementären Anordnung – ebenfalls 33 und 22:

	2		3			3			2		ZS	FS
Punkte	1		3		5	6		8		10	33	27
Linien		2		4			7		9		22	19
											55	46

Die ZS 55 hat eine parallele Entsprechung in 5+5 Radialelementen, die FS 46 in 4 Linien + 6 Punkten.

Das Umkehrmuster 23/32 zeigt sich auch in der Summe der Faktorenwerte (FW) der Punkte- und Liniensummen:

	P		L
	ZS	FS	ZS	FS
	33	27	22	19
FW	14	9	13	19
	23		32

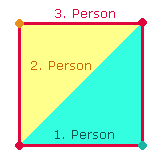
4. Die Numerierungssummen 36 und 48 weisen auf die geometrischen Figuren des Dreiecks und des Quadrats hin: das Dreieck mit 3*(1L+2P), das Quadrat mit 4*(1L+2P). Man kann also der 1. und 2. Person Dreiecke zuweisen, die von der 3. Person in Form eines Quadrats umfaßt werden:

5. Die 2. Person ist das vollkommene Abbild der 1. Person und hat daher dieselbe ZS 36, die FS beider unterscheiden sich jedoch. Das Verhältnis 3*(10:11) weist der 1. Person einmal, der 2. Person zweimal die 1 zu.

6. Addiert man die ZS und FS der linken und rechten DR und setzt sie ins Verhältnis zu den Werten der mittleren DR, erhält man identische Verhältniszahlen:

72:48 = 24*(3:2)

63:42 = 21*(3:2)

Damit bestätigt sich die im ersten Teil ermittelte Gleichung 2:1 = 3:2. Das doppelte Verhältnis 3:2 läßt sich auf die 2*(3+2) Radialelemente des Doppelkreises beziehen.

Das Verhältnis der addierten FS:ZS 105:120 = 15*(7:8) weist auf zwei Doppelrauten hin, aus denen ein Oktaeder zusammengesetzt werden kann.

7. Fortsetzung zur ZW/FW-Verrechnung

Erstellt: Februar 2007

Inhalt