Umkehrungen dreistelliger Zahlen

I. 6 Umkehrungen

II. Teilungen durch 11

III. Die übrigen dreistelligen Zahlen

IV. Umkehrungen von Produkten aus 12, 13, 14, 23

V. Faktor 37

I. 6 Umkehrungen

1. Von jeder dreistelligen Zahl aus drei verschiedenen Ziffern können 6 Umkehrungen (Uk) gebildet werden. Die Summe der Umkehrungen bestimmt sich nach der Quersumme (QS) der Ziffern:

Sm(Uk) = 2QS*3*37 = 2QS*111 oder QS*222

2. Je zwei Umkehrungen gehören einer Hunderter-Einheit an. Die niedrigere Zahl sei mit 1, die höhere mit 2 bezeichnet. Die drei Hunderter-Einheiten seien eine aufsteigende Folge.

Die Sm(Uk) läßt sich in zwei Hälften aufteilen nach dem Umkehrungsmuster 121 + 212.

3. Teilungsbeispiel seien die Umkehrungen der Zahl 123:

				sm				sm	GS
1	123		312	435		213		213	648
2		231		231	132		321	453	684
sm				666				666	1332

Bei jeder folgende Umkehrung wird die vordere Ziffer nach hinten gestellt, sodaß jede der drei Ziffern vorne, in der Mitte und hinten einmal vertreten ist und so durch 111 = 3*37 teilbar ist. Diese Anordnung ist zweimal möglich.

Die horizontalen Summen sind mindestens durch drei teilbar. Bei der Ausgangszahl 123 ist der gemeinsame Teiler der beiden Teilsummen jeweils 3*QS = 36, die Zahl 37 wird aufgeteilt in ihre Konstitutiven 18+19:

648:684 = 36*(18:19)

4. Von Interesse sind die Umkehrungen durch ihre Faktorenwerte (FW), wie exemplarisch an den Umkehrungen von 123 gezeigt werden soll:

				sm				sm	GS
Z	123	231	312	666	132	213	321	666	1332
FW	44	21	22	87	18	74	110	202	289
sm				753				868	1621
289 = 17*17

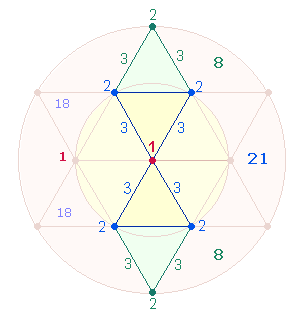
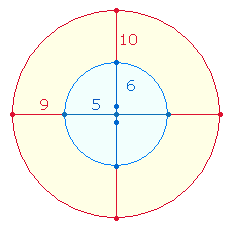
Die Faktorensumme (FS) 87+202 = 289 = 17*17 kann aufgeteilt werden in 2*(8+9) = 2*17 = 34. Bezugspunkt sind zwei Oktaederhälften aus 8 Elementen für die gemeinsame Mittelbasis und 9 Elementen für den pyramidenförmigen Aufbau.

Die FS der ersten und der zweiten Hälfte der Umkehrzahlen in aufsteigender Ordnung bilden ein Zahlenverhältnis:

				sm	FW	sm				sm	FW	sm	GS
Z	123	132	213	468	23		231	312	321	864	19
FW	44	18	74	136	23		21	22	110	153	23
sm				604	46	650				1017	42	1059	1709
136:153 = 17*(8:9); 604 = 4*151; 1017 = 9*113

Der Verhältnisausdruck 17*(8:9) zeigt die Zusammensetzung zweier Oktaederhälften, die Gesamtsumme 1709 die Elemente einer Oktaederhälfte und 9 Elemente für den Aufbau der zweiten Pyramide, also die 26 Elemente des Oktaeders.

Die ZS+FS der 6 Umkehrungen ist 1332+289 = 1621. Die Aufteilung der Primzahl 1621 in 16+21 gibt die Numerierungssumme 37 der Rahmenelemente einer Doppelraute des Tetraktyssterns wieder, wobei sich 21 auf den hexagonalen und 16 auf den Erweiterungsbereich bezieht:

Die Einzelziffern weisen auch auf die 1+6 Punkte des Hexagons und 2+1 Eckpunkte der Tetraktys hin.

5. Dreistellige Basiszahlen mit drei verschiedenen Ziffern lassen sich in zwei Gruppen einteilen: Die erste reicht bis 5 und ermöglicht eine gleich Zahl von Komplementärzahlen:

123	124	125	134	135	145
234	235	245
345
987	986	985	976	975	965
876	875	865
765

Das Summenverhältnis der zweimal 10 Zahlen beträgt 1845:9255 = 15*(123:617) = 15*740 = 11100.

Die zweite Gruppe reicht über 5 hinaus:

126	127	128	129	236	237	238	239	346	347	348	349	456	457	458	459
136	137	138	139	246	247	248	249	356	357	358	359		467	468	469
146	147	148	149	256	257	258	259		367	368	369			478	479
156	157	158	159		267	268	269			378	379				489
	167	168	169			278	279				389
		178	179				289
			189

Die beiden Tabellen enthalten 20+64 = 84 Zahlen, die mit 6 zu 504 = 9*8*7 zu multiplizieren sind. Auf jede der 9 Hundertereinheiten entfallen somit 56 = 8*7 dreistellige Zahlen mit verschiedenen Ziffern.

Das Summenverhältnis der zwei linken zu den zwei rechten Reihen der zweiten Gruppe beträgt 7950:9750 = 150*(53:65) = 300*59 = 17700. Das Summenverhältnis der zwei rechten Reihen beträgt 5070:4680 = 390*(13:12).

II. Teilungen durch 11

1. Liest man eine durch 11 teilbare 3-stellige Zahl von hinten nach vorne, ist diese Umkehrung ebenfalls durch 11 teilbar:

143	341	198	891	495	594
13*11	31*11	18*11	81*11	45*11	54*11

In den angeführten Beispielen wird auch die zweite Produktzahl umgekehrt. Dies ist aber nur bei der Hälfte der Zahlen der Fall. Bei der anderen Hälfte ist von der höheren zweistelligen Umkehrzahl 9 abzuziehen, z.B. 91-9 = 82:

209	902	319	913	638	836
19*11	82*11	29*11	83*11	58*11	76*11

Ausgangszahlen der zwei Reihen sind 121 und 209, die fortgesetzt werden durch 242, 363, 484 bzw. 308, 407, 506:

209		121	132	143	154	165	176	187	198
902			231	341	451	561	671	781	891
308	319			242	253	264	275	286	297
803	913				352	462	572	682	792
407	418	429				363	374	385	396
704	814	924					473	583	693
506	517	528	539					484	495
605	715	825	935						594
	616	627	638	649
		726	836	946
			737	748	759
				847	957
					858	869
						968
							979

2. Jede Reihe besteht aus 36 Zahlen. Das Summenverhältnis der rechten zur linken Reihe beträgt 14520:25080 = 12*110*(11:19) = 39600. Der Verhältniszahl 11 entspricht ein Basisachsenkreuz mit einem und zwei Mittelpunkten, die Verhältniszahl 19 stellt ein erweitertes Achsenkreuz dar:

Die zweimal 36 Zahlen bilden paarweise Komplementärsummen zu je 1100, z.B. 121+979, 132+968, 231+869, wie der folgenden Tabelle zu entnehmen ist:

		121	132	143	154	165	176	187	198
209			231	242	253	264	275	286	297
308	319			341	352	363	374	385	396
407	418	429			451	462	473	484	495
506	517	528	539			561	572	583	594
605	616	627	638	649			671	682	693
704	715	726	737	748	759			781	792
803	814	825	836	847	858	869			891
902	913	924	935	946	957	968	979

III. Die übrigen dreistelligen Zahlen

1. Von 100 bis 999 sind es 900 Zahlen. Zu Zahlen mit drei verschiedenen Ziffern gehören auch solche mit einer 0. Sie haben auf dreistelliger Ebene nur vier Umkehrungen. Wenn die Null am Anfang steht, werden auch zweistellige Zahlen erfaßt. Zur Ermittlung der Zahlen beginnt man mit 102 bis 109, dann 203 bis 209 bis 809. Auf diese Weise erhält man 36 Zahlen, mit 4 multipliziert, 144.

2. Ist eine Ziffer zweimal in einer dreistelligen Zahl enthalten, gibt es nur drei Umkehrungen. Als Muster diene die Reihe 112-119. Jede Hundertereinheit enthält eine fortlaufende Reihe von 8 Zahlen, von denen zwei gleich sind. Zu jeder gibt es zwei Umkehrungen, z.B. 121 und 211. Auf diese Weise erhält man 3*9*8 = 216 Zahlen.

Kommt zu zwei gleichen Zahlen eine 0 hinzu, gibt es nur zwei Umkehrungen, z.B. 101, 110. Auf diese Weise erhält man 18 Zahlen.

3. Zahlen mit drei gleichen Zahlen wie 111 sowie die vollen Hunderter sind nicht umkehrbar. Die Summe sind weitere 18 Zahlen.

4. Die 900 Zahlen setzen sich nun folgendermaßen zusammen:

Umk.	einzeln	xUmk.	Beisp.
6	84	504	123
4	36	144	102
3	72	216	112
2	9	18	101
0	18	18	100, 111
	219	900

Erstellt: Februar 2011

Ergänzt: Mai 2015

Inhalt