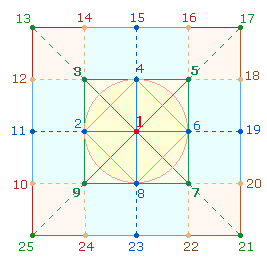
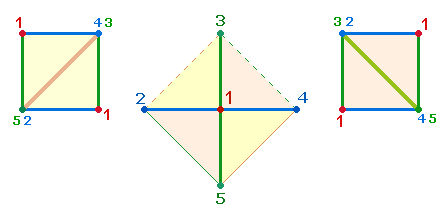
D. Numeriertes 5*5 Quadrat, 1x1 Quadrat und SATOR-Quadrat
Einheit
dreier Quadrate
IV. Das Verhältnis der Winkelpunkte
1. Die
Untersuchung konzentrischer Quadratrahmen (QR) und ihre
Numerierung ließ die Bedeutung der Winkelpunkte = Eckpunkte + 2 Randpunkte
erkennen. Dabei steht 1 Eckpunkt des kleineren QR in Beziehung
zum Eckpunkt des größeren QR und dessen 2 benachbarten
Punkten:
|
|
Es entstehen
auf diese Weise Beziehungen der Punktewerte im Verhältnisse 1:1, 1:3, 2:2 und 1:2.
2. Die
Zusammengehörigkeit von Zahlengruppen erkennt man vornehmlich am Zustandekommen
von gemeinsamen Teilern.
Aufgrund der
Palindromstruktur des 1x1-Quadrats (1x1Q) und des SATOR-Quadrats (SQ) sind die Werte der vertikalen und horizontalen Quadratseiten jeweils
gleich. Es kommen also nur die Diagonalen für Zahlenverhältnisse in Frage.
3. Ein Problem
der 3 Quadrate ist, ob ihre Ecken einander eindeutig zuzuordnen
sind und wenn ja, wie die Quadratseiten richtig zueinander stehen. Die
originalen Funde des SATOR-Quadrats beginnen horizontal mit dem
Umkehrwort ROTAS. Im Lateinischen werden Zahlenreihen von unten
nach oben geschrieben, weswegen das Additionsergebnis die höchste Position
einnimmt, eben die "Summe". Die Einerstellen des 1x1Q, das mit 3*3 = 9 einsetzt und
mit 7*3 = (2)1 endet, ist
also von unten nach oben anzuordnen. Die Zuordnung zu den Buchstabenwerten
ergibt durch S = 18+9 = 27 und R = 17+1 = 18 ein sinnvolles, durch 9 teilbares
Zahlenverhältnis.
Die
Numerierung des 5*5-Quadrats (NQ) kann nach zwei Richtungen hin beginnen. Ich habe die Zahl 2 links vom
Mittelpunkt gesetzt und bin im Uhrzeigersinn fortgefahren.
4. In der von
mir gewählten Zuordnung der Quadrate ist in chiastischer Form ein Zahlenverhältnis
der ZS+FS der 4*4 Punktewerte zustande gekommen. Es soll im folgenden dokumentiert werden:
|
|
ZS |
FS |
GS |
ZS |
FS |
GS |
|
NQ |
42 |
32 |
74 |
56 |
38 |
94 |
|
1x1 |
21 |
17 |
38 |
19 |
15 |
34 |
|
SQ |
60 |
43 |
103 |
37 |
27 |
64 |
|
|
123 |
92 |
215 |
112 |
80 |
192 |
|
NQ |
68 |
32 |
100 |
70 |
39 |
109 |
|
1x1 |
19 |
15 |
34 |
21 |
17 |
38 |
|
SQ |
37 |
27 |
64 |
60 |
43 |
103 |
|
|
124 |
74 |
198 |
151 |
99 |
250 |
Die
diagonalen Werte sind unter sich durch 5 und 6 und in der Addition durch 15 teilbar:
|
D1 |
215:250 |
5*(43:50) |
|
D2 |
198:192 |
6*(33:32) |
|
D1:D2 |
465:390 |
15*(31:26) |
Die Zahlen 5 und 6 beziehen sich auf die 5 Zahlen des
Achsenkreuzes und 6 Zahlen der Quadratnumerierung nach
Verschiebung der Winkel, die Zahl 15 auf die
Summe der Zahlen von 1-5. Die diagonalen Summen sind durch
die Umkehrzahlen 31 und 13 teilbar und bekunden somit das Verhältnis der Eckpunkte
des inneren QR zu je 3 Winkelpunkte
des äußeren QR.
Die vertikale
Addition der Verhältniszahlen ergibt zwei benachbarte Zahlen und die Summe der
linken oberen Ecke: 107+108 = 215.
5.
Ein Verhältnis 11:15 erhält man,
wenn man von den oben ermittelten Einzelsummen die Faktorenwerte (FW) bildet und sie dazurechnet:
|
|
ZS |
FS |
Sm. |
FW1 |
FW2 |
Sm. |
GS |
|
o.li. |
123 |
92 |
215 |
44 |
27 |
71 |
286 |
|
o.re. |
112 |
80 |
192 |
15 |
13 |
28 |
220 |
|
|
235 |
172 |
407 |
59 |
40 |
99 |
506 |
|
u.li. |
124 |
74 |
198 |
35 |
39 |
74 |
272 |
|
u.re. |
151 |
99 |
250 |
151 |
17 |
168 |
418 |
|
Sm. |
275 |
173 |
448 |
186 |
56 |
242 |
690 |
|
GS |
510 |
390 |
855 |
|
|
341 |
1196 |
Von den 4 Gesamtsummen sind 3 durch 11 teilbar, ihr Gesamtergebnis ist 84*11. In der Produktaufteilung 4*21 kommt in der Zahl das Verhältnis von
2 Punkten zu 1 Linie je Quadratseite zum Ausdruck.
Das
Verhältnis der beiden FW1/FW2-Summen ist 99:242 = 11*(9:22).
Das
Verhältnis der beiden Gesamtsummen 506 und 690 zueinander ist 2*23*(11:15).
Die Faktoren 11*31 = 341 bezeichnen genau den Vorgang der
Umwandlung eines numerierten Achsenkreuzes in ein Quadrat und die Addition
dieses Vorgangs: 5+6 Zahlen mit den Summen 15+16. Die Ziffern 341 beschreiben einen
Vereinigungsvorgang, bei dem eine Ecke aus 3+4 = 7 besteht (in
der linken Grafik von links nach rechts zu lesen) und die nächste die 1 des Mittelpunktes erhält:
|
|
Erstellt:Januar 2008