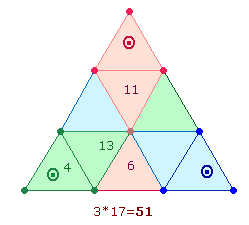
6 numerierte konzentrische Quadrate bis 169

Sechs numerierte konzentrische Quadrate

a) Die diagonalen Achsen

1. Unter dem Urknall stellt sich der Laie etwa vor, daß vor 13 Milliarden Jahren, von einem einzigen Punkt ausgehend, eine gewaltige Energieexplosion geschah, die nach allen Richtungen ausstrahlend den dreidimensionalen Kosmos schuf, den wir heute bewundern. Eine Explosion hat zwar annähernd berechenbare Auswirkungen, schafft jedoch nichts Neues. Von jener Urknallexplosion möchten wir jedoch vermuten, daß sie in höchster Ordnung ablief oder wenigsten sich zu höchster Ordnung über die Zeiten hinweg fügte.

Der Ausgangspunkt allen Zählens ist die Zahl 1. Also wird man auch die Urknallexplosion als eine 1 ansehen können, von der aus sich die Zahlen in geordneter Folge und ungeheuerer Geschwindigkeit zu gewaltiger Größe ausbreiteten.

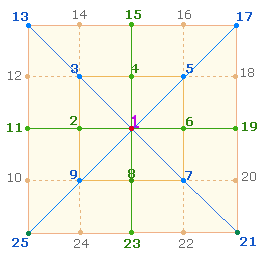
2. Als abbildhaftes Modell dieses Vorgangs bietet die Geometrie das Quadrat an. Ausgangspunkt der Konstruktion sind zwei Geraden im rechten Winkel, die man im gleichen Abstand nach den vier Richtungen absteckt. Durch zwei horizontale und vertikale Parallelen erhält man vier Schnittpunkte als Eckpunkte des Quadrats, durch die man zwei diagonale Geraden ziehen kann:

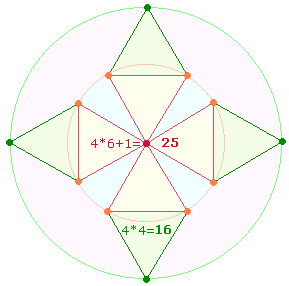
Ein solches Quadrat enthält 9 Punkte, die man der Reihe nach numerieren kann. Wenn man, wie hier, die Zahl 2 links vom Mittelpunkt auf die Horizontalachse setzt und im Uhrzeigersinn fortfährt, endet die Numerierung links unten mit 9, dem Quadrat von 3. Alle ableitbaren Numerierungsregeln sind auf die erste Festlegung bezogen. Man kann nämlich die Zahl 2 auf einen der anderen 7 Rahmenpunkte setzen. Unter der gewählten Option ist die Numerierungssumme des horizontal-vertikalen Achsenkreuzes (ohne Mittelpunkt) um 4 kleiner als die Summe der diagonalen Eckpunkte.

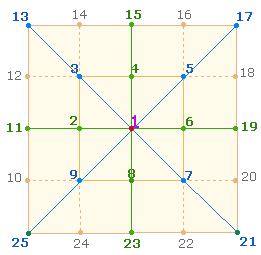
Zu weiterer Numerierung ist das Ausgangsmaß zweimal auf der horizontalen oder vertikalen Achse abzustecken und Parallelen durch die Diagonalgeraden zu ziehen, außerdem die vorhergehenden Quadratseiten von ihren 4 Eckpunkten aus zu verlängern:

Die Numerierung des zweiten Quadratrahmens endet wieder mit einer Quadratzahl, mit 25, dem Quadrat von 5. Daraus lassen sich die ersten Regeln ableiten:

· Der Abstand von einer Quadratzahl zur nächsten erhöht sich jeweils um die Zahl 8. Die Zahl 1 des Mittelpunktes ist demnach als Quadratzahl anzusehen. Der Abstand von 1 bis 9 beträgt 8, zur nächsten Quadratzahl ist der Abstand dann 8+8.

· Es kommen also mit jedem Quadratrahmen 8 Punkte hinzu. Diese befinden sich vor und nach den 4 Eckpunkten des größeren Quadrats. Sie können als vorausgehende und nachfolgende Randpunkte bezeichnet werden. Aus diesem Grund ist die Diagonalachse von herausragender Bedeutung.

· Mit jedem Quadratrahmen wird die Summe der 4 Diagonalpunkte um 4 größer als die der horizontal-vertikalen Achsenpunkte.

· Die Summe der Randpunkte ist an sich doppelt so groß wie die der Eckpunkte. Aber oberhalb der Quadratzahl, hier 25, folgt nicht 26, sondern 10, die Nachfolgezahl der vorhergehenden Quadratzahl 9. Die Summe der Randzahlen ist also beim ersten Mal um 16 kleiner als die doppelte Zahl der Eckpunkte, also 2*76 = 152-16 = 136. Der Abstand vergrößert sich um 8 bei jedem weiteren Quadratrahmen.

· Die Summe eines Quadratrahmens ist stets durch 4 teilbar.

3. Entsprechend diesen Regeln ergeben sich für das Qu13 folgende Summen:

· Die Quadratzahlen ergeben sich aus fortlaufender Addition von 8:

		+8	+16	+24	+32	+40	+48
	1	9	25	49	81	121	169
FW	1	6	10	14	12	22	26	91
fl.Add.	1	10	35	84	165	286	455
25:35 = 5(5:7); 49:84 = 7(7:12); 121:286 = 11*(11:26)
169:455 = 13(13:35); 35:84 = 7(5:12); 91:455 = 713(1:5)
165:286 = 11(15:26); 286:455 = 13(22:35)

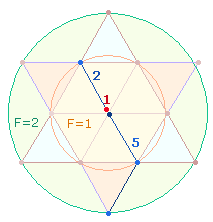
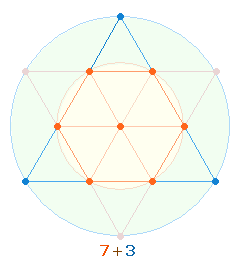
91 ist die Summe der Zahlen 1-13 und somit auf die 13 Punkte des Hexagramms beziehbar. Die 7 Punkte des Hexagons und 13 Punkte des Hexagramms geben das trinitarische Kreisflächenverhältnis 1:3 wieder.

Die Summen der Zahlen von 1 bis zur jeweiligen Quadratzahl (1-25, 1-49 usw.) werden durch Multiplikationen ermittelt. Gegenüber der vorhergehenden Multiplikation beträgt die Differenz des kleineren Multiplikators fortlaufend jeweils die Hälfte des höheren:

		fl. Add.	Fakt.	FW	fl. Diff.	Rahmen	Fakt.	FW
1*1	1	1				(1)	1*1	1
9*5	45	46			8 4	44	4*11	15
25*13	325	371			16 8	280	4*70	18
49*25	1225	1596			24 12	900	4*225	20
81*41	3321	4917	311149	163	32 16	2096	16*131	139
121*61	7381	12298	21113*43	69	40 20	4060	140*29	45
169*85	14365	26663	713293	313	48 24	6984	72*97	109
	26663					14364		347
14364 = 108133 = FW 13+26 = 39 = 313

Die Primzahl 347 ist eine bedeutende Dreifaltigkeitszahl. Die Primzahl 313 gibt die Punktestruktur der DR wieder.

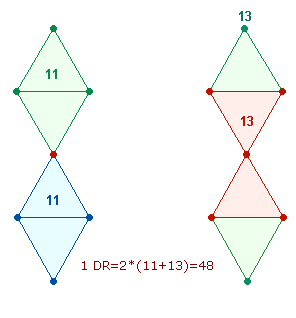
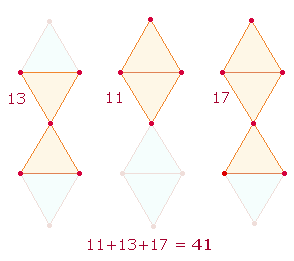
Bei Aufaddierung der Multiplikationsergebnisse fällt ein Vorausgehen der Faktoren 11 und 13 auf. Beiden Faktoren entsprechen die Elemente zweier geometrischer Figuren, die für die Oktaederbildung aus einem Doppelrautenkreuz konstitutiv sind:

Das sanduhrförmige Doppeldreieck der rechten Seite wird bei Zusammenführung der äußeren Punkte ein zweites Mal gebildet.

Die Zahl 81 bedeutet in seinen Einzelziffern 8 symmetrische Durchmesserelemente der Zickzacklinie der Doppelraute (DR) und der Mittelpunkt. Es gibt zwei Zickzacklinien, die durch 9*9 dargestellt werden können, aber auch auch die eingeschlossenen vertikalen Mittelelemente lassen sich von 1-9 zählen. Da es im Tetraktysstern drei DR gibt, ist 9*9 = 81 Elemente auch eine reale Zahl.

Die Zahl 121 = 11*11 stellt die Doppelraute dar, die sich bei der hexagonalen Erweiterung aus dem Doppeldreieck entwickelt. Wie die Abbildung zeigt, ist 2*11*13 als 2*(11+13) interpretierbar. Aus 43 Elementen besteht ein DR-Kreuz mit 3 Mittelpunkten.

· Die Summen der linken oberen und unteren sowie rechten oberen und unteren Eckpunkte sind in der Addition jeweils gleich. Geht man vom linken Eckpunkt aus, so ist der Abstand zwischen der 1 des Mittelpunktes und der 3 des Eckpunktes 2, der Abstand zum nächsten Eckpunkt ist 2+8 = 10, der nächste Eckpunkt also 13, danach erhöht sich der Abstand um jeweils 8, also 10+8 = 18, der Eckpunkt ist 31. Die linke untere Zahl ist die jeweilige Quadratzahl:

Qu.	1	2	3	4	5	6
Abst.	2	10	18	26	34	42
1	3	13	31	57	91	133
	9	25	49	81	121	169
	12	38	80	138	212	302
dopp.	24	76	160	276	424	604	1564

Um die Summen der Randpunkte zu bestimmen, muß man mit dem zweiten Quadrat beginnen und 24 von 1564 abziehen. Die vorangehenden Punkte betragen demnach 1540 – 5*4 = 1520. Für die vorangehenden Randpunkte gilt 1540+20 = 1560. Davon abzuziehen sind die Unterzahlen der unteren linken Punkte, wie oben dargelegt. Abzuziehen sind somit die Zahlen von 5 Quadratrahmen: 16+24+32+40+48 = 160. Die Summe der vorangehenden Randzahlen ist demnach 1560-160 = 1400.

Fügt man zur Summe 1564+1520+1400 = 4484 noch die 1 des Mittelpunktes, erhält man für 3*(5*4)+4+1 = 60+5 = 65 = 5*13 Zahlen und die Gesamtsumme 4485 die Faktoren 3*5*13*23 = Faktorenwert (FW) 13+31 = 44. Die Durchschnittszahl je Punkt ist demnach 3*23 = 69. Das ZS-Verhältnis der 65:104 = 13*(5:8) Zahlen beträgt 4485:9880 = 65*(69:152) = 65*221.

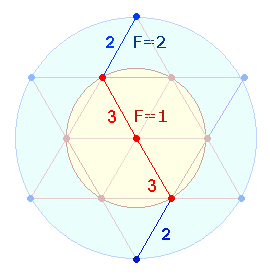
Bemerkenswert ist die Summe 1520, das Zehnfache der Verhältniszahl 152. Fügt man ihr die Mittelpunkt 1 hinzu, erhält man mit 1521 das Produkt 3*13*3*13 = FW 32. Zweimal 3*13 weist auf die Punktestruktur eines DR-Kreuzes hin, ebenso 32 = 2⁵ auf zwei Erweiterungspunkte und 5 Punkte des hexagonalen Bereichs. Auch der FW von 1520 ist 32: 80*19 = 13+19. Hier ist einerseits an die Punkteaufteilung zweier DR zu denken, andererseits an zweimal 3+2 Radialelemente des Hexagrammdurchmessers:

3:2 Radialelementen entspricht das Kreisflächenverhältnis 1:2. Die Eckpunkte und die Randpunkte bilden jeweils das Verhältnis 1:2. Offensichtlich übernehmen die nachfolgenden Randpunkte die Aufgabe, dieses Verhältnis darzustellen.

Die Zahl 19 setzt sich zusammen aus 10+9, den Komplementärzahlen zu 1+2. 10+9 stellen die Radialelemente und Durchmesserelemente der DR dar. Die FW der beiden Zahlen sind 7+6 = 13. Auf die 13 Punkte des Tetraktyssterns bezogen bedeuten 7+6 wiederum das Kreisflächenverhältnis 1:2, und als zusammengesetzte Zahl 76 sind ihre Faktoren 4*19 = FW 23. Einzeln ergeben die zwei Komplementärzahlen zusammen mit ihren FW 10+7 = 17 und 9+6 = 15. Darauf weisen die Einzelziffern von 152 = 15+2 hin. Das sanduhrförmige Doppeldreieck besteht aus 5 Punkten und 2 Dreiecken = 7 Elementen und 6 Linien. Der FW von 152 beträgt 25, die Zahl der Elemente eines Kreuzes aus zwei Doppeldreiecken als Basis für das DR-Kreuz:

Die ZW/FW-Verrechnung der beiden Summen 1520 und 1521 führt zu folgenden Ergebnissen:

			sm	FW	sm	FW
ZS	1520	1521	3041	3041
FW	32	32	64	12
sm			3105	3053	6158	3081
FW			37	114	151	151
sm						3232

Die Einzelziffern der Primzahl 151 weisen auf die Punkte der DR hin, 3232 führt zu den FW der Zahlen 1520 und 1521 zurück.

b) Die Zahlensummen der vier Achsen

1. Die ZS der 4 diagonalen und 4 horizontal-vertikalen Achsenarme sind:

diag.	328	370	412	454	1564
h.-v.	307	349	391	433	1480
					3044

Die Summe der Zahlen von 1-6 ist 21. Da es sich um 6 konzentrische Quadrate handelt, ist der Summenabstand von einem Achsenarm zum andern 21. Fügt man zu jeder der 8 Summen die 1 des Mittelpunktes hinzu, ist jede durch 7 teilbar:

diag.

224

h.-v.

212

Mit einem Mittelpunkt ist die ZS der 49 Achsenzahlen 3045 = 15*203 = 3*5*7*29 = 105*29. 7 Zahlen haben somit die Durchschnittssumme 435 = 15*29, die Summe der Zahlen 1-29.

2. Zahlenverhältnisse sind als ein Beweis für die Objektivität eines vermuteten und ausgeführten Ordnungssystems anzusehen. Die Summen der 49 Achsenzahlen können in jeweils 13 horizontalen und vertikalen Reihen ermittelt werden:

133						139						145	417
	91					96					101		288
		57				61				65			183
			31			34			37				102
				13		15		17					45
					3	4	5						12
127	86	53	28	11	2	1	6	19	40	69	106	151	699
					9	8	7						24
				25		23		21					69
			49			46			43				138
		81				77				73			231
	121					116					111		348
169						163						157	489
429	298	191	108	49	14	783	18	57	120	207	318	453	3045

Die Summen 783 und 348 sind durch 29 teilbar, wie auch die Koordinatensumme 116. Es ergibt sich somit die Summe 783+348-116 = 1015. Es bleibt übrig die doppelte Summe 2030.

Die vertikalen Summen ermöglichen zwei durch 105 teilbare Summen: 1890:1155 = 105*(18:11), 525 = 5*105; 2415:630 = 105*(23:6).

Drei horizontale Summe sind zusammen durch 105 teilbar: 735 = 7*105. 7 horizontale Summen, die die drei durch 105 teilbaren einschließen, sind durch 29 teilbar: 1218:1827 = 406*(2:3).

Fügt man die nachfolgende Summe 348 hinzu, ist das Verhältnis 1566:1479 = 87*(18:17).

3. Die Summen der 6 Quadratrahmen erlauben zwei Zahlenverhältnisse. Die 1 des Mittelpunktes steht jedem Rahmen zur Verfügung:

1	44	144	308	536	828	1184	3045
145:580 = 529(1:4); 725:2320 = 145*(5:16)

Beim zweiten Zahlenverhältnis verbindet sich die 1 des Mittelpunktes mit dem ersten Rahmen:

1	44	144	308	536	828	1184	3045
1537:1508 = 29*(53:52)

c) Die Faktorensummen der vier Achsen

1. Auch die FW der 49 Achsenzahlen zeigen eine bemerkenswerte Ordnung:

26						139						34	199
	20					13					101		134	9x
		22				61				18			101	188
			31			19			37				87
				13		8		17					38
					3	4	5						12	17x
127	45	53	11	11	2	1	5	19	11	26	55	151	517
					6	6	7						19
				10		23		10					43
			14			25			43				82	5x
		12				18				73			103
	22					33					40		95	441
26						163						157	346	17x
179	87	87	56	34	11	513	17	46	91	117	196	342	1776
353			768 = 1648+2148							655

Die Faktoren 48*37 der Gesamtsumme 1776 sind in Zahlenverhältnissen der vertikalen und horizontalen Summen zu finden:

Konzentrisch haben die 6 äußeren vertikalen Summen zu den 7 inneren das Verhältnis 1008:768 = 48*(21:16). Die Verhältniszahlen können sich auf die Elemente eines DR-Kreuzes oder auf die Numerierungssummen der Rahmenelemente der DR beziehen. In beiden Fällen geht es um das Verhältnis von hexagonalen zu Erweiterungselementen als Kreisflächenverhältnis 1:2.

2. Die Zahlenverhältnisse der durch 37 teilbaren horizontalen Summen sind komplexer. In konzentrischer Position haben 5 innere zu 8 äußeren Summen das Verhältnis 17:31. Insbesondere sind zwei Verhältnisse 22:26 erkennbar, zu beziehen auf zwei Rauten und Doppeldreiecke, aus denen der Oktaeder besteht, wenn man ihn aus einem DR-Kreuz zusammensetzt:

1	2	3	4	5	6	7	8	9	10	11	12	13
199	134	101	87	38	12	517	19	43	82	103	95	346
814:962 = 37*(22:26)

Dem Verhältnis 22:26 entsprechen die Positionssummen 56 und 35.

1	2	3	4	5	6	7	8	9	10	11	12	13
199	134	101	87	38	12	517	19	43	82	103	95	346
333:629 = 37(9:17); 814:962 = 37(22:26)

Dem Verhältnis 22:26 entsprechen die Positionssummen 53 und 38.

Die Addition der Positionssummen ergibt für 22 109 und für 26 73. Numeriert man den Mittelpunkt des Hexagons mit 1, die Kreislinienpunkte mit 2, die Linien mit 3 und die Flächen mit 4, ergeben sich für das Hexagon und die Tetraktys die Summen 73 und 109.

Das doppelte Verhältnis 22:26 ist darin sinnvoll, daß jeweils vier Rauten und vier Doppeldreiecke allein den Oktaeder zusammensetzen.

3. Die 13 Summen bestehen aus 3 zusammenhängenden durch 37 teilbaren Blöcken:

1	2	3	4	5	6	7	8	9	10	11	12	13
199	134	101	87	38	12	517	19	43	82	103	95	346
9				17					5

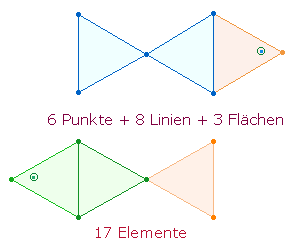
Die Faktoren 9+17+5 = 31 lassen sich auf die 17 Elemente der "Fischfigur" und ihrer FS beziehen:

Die FW von 3, 6 und 8 sind 3+5+6 = 14. Im Faktor 9 sind die Flächen und Linien zusammengefaßt.

Für das Verhältnis 31:17 kann ich keine sichere Lösung vorlegen. Denkbar ist folgendes: 31 und 17 setzen sich aus dem ZW+FW der Zahlen 21+10 = 31 und 10+7 = 17 zusammen. Aus 21 Elementen besteht die DR , aus 10 Punkten die Tetraktys, aus 7 Punkten das Hexagon. Aus der Zahl 21 ergeben sich so gewissermaßen absteigende Definitionen. Das oben genannte Verhältnis 22:26 liegt in den zweimal zwei Buchstaben des Wortes HOMO – Mensch vor. 17 ist dort die Differenz zwischen FS und ZS:

	H	O	sm	M	O	sm	GS
ZW	8	14	22	12	14	26	48
FW	6	9	15	7	9	16	31
sm	14	23	37	19	23	42	79

4. Die Summen der Positionen 3 und 4 sowie 12 und 13 ergeben wie 5-9 17*37. Es wird eine innere Beziehung der Positionen darin erkennbar, daß 3 und 4 die Summen von 1+2 und 1+3 sind. Als Bezugspunkt sind die Kreisflächenverhältnisse 1:2 und 1:3 der beiden konzentrischen Hexagrammkreise zu verstehen. Aus 7+6 = 13 Punkten und 6+6 = 12 Flächen bestehen Hexagon und seine Erweiterung. In dieser Kombination geben 13+12 Elemente das Kreisflächenverhältnis 1:2 wieder.

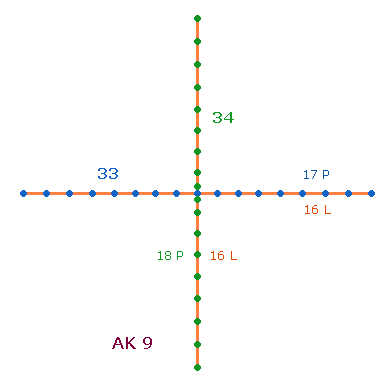
Die Addition der Positionen der beiden durch 17 teilbaren Summen beträgt 32 und 35. Bildet man ein Achsenkreuz, dessen vier Achsenarme aus jeweils 9 Punkten und 8 Linien und deren zwei Achsen aus jeweils 17 Punkten und 16 Linien bestehen, und ordnet man der zweiten Achse zwei Mittelpunkte zu, erhält man 35 Punkte und 32 Linien:

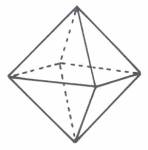
5. Der zweimalige Faktor 17 ist auf den Oktaeder zu beziehen:

Der Oktaeder besteht aus zwei pyramidalen Aufbauten von jeweils 9 Elementen und eine gemeinsame quadratischen Mittelbasis von 8 Elementen. Eine einzelne Pyramide besteht somit aus 17 Elementen, für die zweite Hälfte sind dann noch 9 übrig.

6. Die FS 1776 ist auffällig, da sie die Summe von 6 Umkehrungen dreistelliger Zahlen ist, deren Quersumme 8 beträgt. Dies ist nur bei den zwei Zahlen 125 und 134 der Fall. Tatsächlich ist die Summe 259 dieser Grundzahlen durch 37 teilbar: 259 = 7*37. Ihre FW 15+69 = 84 bilden das FS:ZS-Verhältnis 84:259 = 7*(12:37). Der Verhältnisdifferenz 25 entsprechen die Elemente des Hexagons und dem Additionsergebnis12+37 die 49 Elemente des Hexagramms.

Aufgeteilt in 25+9 stellt 259 die Punkte der ersten zwei konzentrischen Quadrate dar, denen die beiden konzentrischen Tetraktyskreise entsprechen. Daher sind die Faktoren 7*37 als 7 hexagonale Punkte und 37 als 3+7 erweiterte Tetraktyspunkte zu verstehen. Sie repräsentieren das Kreisflächenverhältnis 1:3. Der FW 44 weist auf 4 Rautenfiguren hin, aus denen der Oktaeder zusammengesetzt ist.

Zwei weitere Umkehrzahlen von 259 sind jeweils durch 37 teilbar: 592 = 16*37, 925 = 25*37. Das Ergebnis ist wiederum 48*37.

Die Einzelziffern der Zahl 125 = 5³ stellen 1+2 und 5 Radialelemente des hexagonalen und Erweiterungskreises des Hexagramms dar und geben das Kreisflächenverhältnis 1:3 wieder:

Die Einzelziffern der Zahl 134 bilden die Gleichung 1+3=4 mit Bezug auf die 2*4 Punkte der DR:

Von beiden Grundzahlen lassen sich 4 Umkehrungen bilden, in denen die genannten Sichtweisen zutreffen:

					sm	FW
UZ	125	215	512	521	1373
FW	15	48	18	521	602	52
UZ	134	314	413	431	1292
FW	69	159	66	431	725	39
1373+1292 = 2665 = 51341 = FW 59
602+725 = 1327

Die Einzelziffern der FW 52 = 4*13 und 39 = 3*13 geben den Doppelaspekt von 8 und 7 Punkten der DR wieder. Der Primzahl 1327 entspricht in dem Produkt 13*27 die Summe der Zahlen von 1-26.

Die Faktoren 48*37 der FS 1776 ergeben wiederum den FW 48. So wirkt die Tetraktys mit ihren 37 Elementen bei der Bildung des Oktaeders mit.

Die Zahl 259 tritt wiederum als FS ihrer beiden Ausgangszahlen in Erscheinung, wenn man zwei Zahlenpaare als rückläufige Umkehrzahlen gruppiert:

			sm	FW	FW	sm
UZ	125	134	259	15	69	84	343
UZ	521	431	952	521	431	952	1904
FW	646	565	1211	536	500	1036	2247
536:500 = 4(134:125) = 4259
565 = 5113; 2247 = 37*107

Die FS der 6 Umkehrzahlen von 134 ist 791 = 7*113.

7. Die FS der 6 Quadratrahmen sind 39+111+191+283+329+823. Die Summe der ersten vier zu den letzten zwei beträgt 624:1152 = 48*(13:24) = FW 24+20 = 44. 44 ist wieder auf die Elemente von vier Rauten zu beziehen. Die Einelziffern der Zahl 24 geben die Maßeinheiten der Kreisachse und der DR–Achse in der Bedeutung des Kreisflächenverhältnisses 1:3 wieder:

d) Die Zahlen 169 und 259

1. Zwischen den Zahlen 169 und 259 besteht eine innere Beziehung, wenn man sie aufteilt in 16+9 und 25+9. Beide nämlich weisen auf die ersten beiden konzentrischen Quadrate hin: Im ersteren Fall ist 16 die Punktezahl des zweiten Quadratrahmens, im letzteren die Punktezahl des äußeren und des inneren Quadrats.

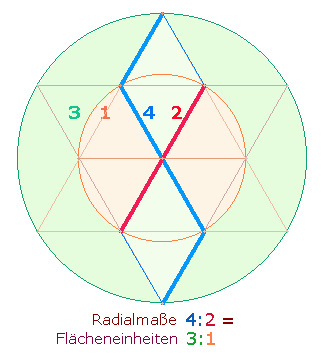
Nun haben aber die beiden konzentrischen Quadrate und die zwei konzentrischen Kreise des Hexagramms so miteinander verbunden, daß die Verhältnisse der einen Konstruktion auf die andere übertragbar sind. Ein Hinweis darauf ist, daß sowohl das Hexagon als auch das erste Quadrat mit Mittelachse aus 25 Elementen besteht. Setzt man also die zweistelligen Zahlen 16 und 25 den beiden Tetraktyskreisen gleich, entsprechen sie 2 und 3 Kreisflächeneinheiten , die zweimalige 9 jeweils 1 Flächeneinheit. Zweistellig zusammengesetzt ergeben die Verhältnisse 2:1 und 3:1 die Zahl 52 = 4*13.

2. Der Zusammenhang der beiden Zahlen wird durch die FS 259 der Umkehrzahlen 169 und 916 bestätigt:

			sm	FW	sm	FW
Z	169	916	1085	43	1085 = 31*35
FW	26	233	259	44
sm			1344	87	1431	62
FW			22	32	54	11
sm						73

Die Einzelziffern der Zahlen 31 und 35 = 7*5 sind als Kreisflächenverhältnis 3:1 als Entsprechung zu 7:5 DR-Punkten zu verstehen; 3:5 Radialelemente der DR bedeuten das Flächenverhältnis 1:3.

Die FW der Zahl 1085 in zweistelliger Aufteilung 10 und 85 sind 7 und 22, addiert 17 und 107. Beide Summen sind als 10+7 in der Bedeutung des Verhältnisses 3:1 zu verstehen. Ihre Addition ergibt 124 = 4*31 und damit das Prinzip 1:2 und 3:1 sich erweiternder konzentrischer Quadrate, das in den 4 Ecken eines Quadratrahmens wirksam ist. Das Ergebnis 17*107 = 1819 enthält die 37 Elemente der Tetraktys: 18 Linien, 10 Punkte + 9 Dreiecksflächen.

Die FS 73 schließlich stellt 7 hexagonale und 3 Erweiterungspunkte dar:

3. Weitere Aufschlüsse erhält man durch die parallele Verrechnung der beiden Zahlen und ihrer (aufgeteilten) Umkehrungen:

			sm
Z	169	259	428
FW	26	44	70
428 = 4*107

Der FW 26 läßt sich auf die 26 Elemente des Oktaeders, der FW 44 auf 4 Rauten beziehen, aus denen der Oktaeder zusammengesetzt ist. Die Faktoren 7*10 geben das Kreisflächenverhältnis 1:3 wieder.

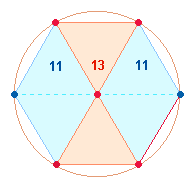
Das Hexagon ist Ausgangsfigur von zwei Tetraktys. Hier ist es gewissermaßen umgekehrt: Das Verhältnis 2*(13:22) = 2*(13+11+11) stellt zwei hexagonale Figurationen für potentiell zwei Tetraktys dar:

Die Ausgangszahlen und Umkehrungen ermöglichen zwei FS-Verhältnisse:

			sm			sm	GS
ZS	169	916	1085	259	925	1184	2269
FW	26	233	259	44	47	91	350
259:91 = 7(37:13); 70:280 = 70(1:4)

Weitere Verhältnisse ergeben sich, wenn man die (nicht zusammengesetzten) Umkehrungen hinzufügt:

				sm				sm	GS
ZS	169	916	961	2046	259	925	952	2136	4182
FW	26	233	62	321	44	47	30	121	442
961+952 = 1913; 952 = 56*17
4182 = 41102 = 61741 = FW 63; 442 = 213*17

1913 ist eine Primzahl, sie kann verstanden werden als 10 Punkte + 9 Dreiecksflächen der Tetraktys und 7 Punkte + 6 Dreiecksflächen des Hexagons und somit das Kreisflächenverhältnis 3:1 repräsentieren.

6*17*41 kann sowohl auf zwei Tetraktys als auch auf drei DR angewendet werden: In jeder Tetraktys sind drei "Fischfiguren" zu erkennen, von denen jede aus 17 Elementen besteht:

In jeder der drei DR können zweimal drei geometrische Figuren erkannt werden, die zusammen 2*41 = 82 Elemente ausmachen:

Auch die Faktoren 2*13*17 enthalten einen Doppelaspekt: Aus 2*13 Elementen besteht ein Oktaeder, aus 2*17 Elementen zwei Oktaederhälften.

Die durchschnittliche ZS der 6 Zahlen beträgt 17*41 = 697. Es ist eine Verbindung von 17 Elementen eines Achsenkreuzes – aus dem ein Quadrat gebildet werden kann – und 41 Elementen eines DR-Kreuzes anzunehmen.

Erstellt: September 2016

Inhalt II