Eigenschaften von Quadraten

Anzahl der Elemente, Numerierung konzentrischer Quadratrahmen

A.

I. Einleitung

II. Das trinitarische Prinzip der Quadratbildung

III. Die trinitarische Bedeutung der Zuwachszahl 8

B. Das numerierte 5*5 Punkte-Quadrat

C. Symmetrien und T-Strukturen des Qu5

I. Einleitung

1. Die Mathematik betrachtet es als ihre vornehmliche Aufgabe, nicht nur Gesetzmäßigkeiten, die in ihren Bereich fallen, festzustellen und anzuwenden, sondern sie auch zu beweisen. Sie stellt jedoch nicht die Frage nach der Herkunft der Gesetzmäßigkeiten. Dies verhindert vor allem die Auffassung, daß es letzte, nicht mehr beweisbare Grundlagen gebe, die man als legitime Ausgangspunkte für mathematische Beweisführung verwenden dürfe. Diese Grundlagen nennt man Axiome. Sie sind so einleuchtend, daß der Gedanke, sie könnten eines transzendenten Ursprungs sein, gar nicht aufkommt.

2. Griechische Mathematiker betrieben ihre Forschungen in der Überzeugung, das der Kosmos von göttlichen Gesetzen bestimmt werde. Heute ist dieser Zusammenhang weitgehend verloren gegangen.

3. Dennoch gilt auch für die Mathematik die allgemeine philosophische Fragestellung: Warum ist etwas und nicht vielmehr nichts? Wenn der Kosmos von einer göttlichen Macht, weder Zeit noch Raum unterworfen, aus dem Nichts geschaffen wurde, so ist es nicht denkbar, daß irgendetwas Geschaffenes nicht nach ihrem eigenen Wesen geschaffen wurde. Wenn aber alles Geschaffene die Prägung des Schöpfers in sich trägt, dann muß er besonders aus auch mathematischen Gegebenheiten erkennbar sein. Dabei ist selbst auf das kleinste Detail zu achten.

4. Details geben also Auskunft über Bedeutung hinsichtlich der Beschaffenheit ihres göttlichen Ursprungs. Man wird diese Details nicht an komplexen Objekten studieren, sondern von ihren einfachsten Modellen ausgehen. Die beiden einfachsten Modelle sind der Kreis und die Zahl.

Der Kreis bildet eine Einheit aus drei untrennbaren Elementen: dem Mittelpunkt, dem Kreisbogen und der von ihm eingeschlossenen Fläche. Dies ist die einfachste Manifestation des einen Gottes in drei Personen. Die Zahlen 1 und 3 sind also feste, wenn auch keineswegs die einzigen Bezugsgrößen des trinitarischen Geheimnisses.

5. Das Verhältnis 1:3 ist auf vielerlei Weisen auch in Quadraten erkennbar. Die Beziehung zwischen Achsenkreuz und Quadrat habe ich in einem allgemeinen Kapitel untersucht. Dort wird auch eine besondere Zielsetzung deutlich: Zahlen erhalten ihre feste Ordnung in einer fortlaufenden Numerierung von Quadratrahmen vom Mittelpunkt aus. Diese Form der Numerierung ist so unbegrenzt wie man sich die Ausdehnung des Weltalls vorstellt.

Die Vorstellung eines konzentrischen Webmusters liegt offensichtlich auch dem SATOR-Quadrat zugrunde, wenn man vom Mittelpunkt aus nach zwei Richtungen liest:NET OPERA SATOR – Es webt die Werke der Schöpfer.

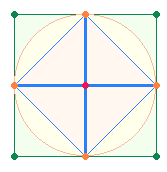
6. Auf das zu numerierende Ausgangsquadrat soll hier noch einmal hingewiesen werden:

Es wirken AK2 und AK3 zusammen. Die im Kreis stehenden 4 Eckpunkte des AK2 lassen sich durch Linien zu einem Rautenquadrat verbinden. Auf dieses Ausgangsquadrat wird sodann ein Quadratrahmen des AK3 gesetzt:

Als praktikabel erweist sich nur die Numerierung von Punkten, nicht jedoch auch der Linien, welche in kreisförmiger Vorgehensweise nicht alle erfaßt würden.

II. Das trinitarische Prinzip der Quadratbildung

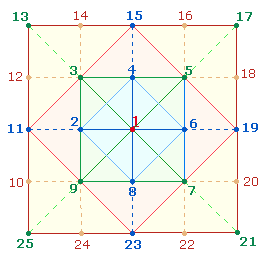
1. Zum Verständnis konzentrisch wachsender Quadrate genügen die ersten beiden Quadratrahmen (QR):

Die Numerierung läßt erkennen, daß jeder Quadratrahmen mit dem Quadrat einer ungeraden Zahl abschließt: 3² = 9, 5² = 25. Rückwärts schließend kann man auch die Zahl 1 des Mittelpunktes (MP) als quadratisch ansehen.

Jeder QR enthält das Quadrat einer geraden Zahl, der erste 2² = 4, der zweite 4² = 16. Die Quadratzahl befindet sich stets unmittelbar vor dem folgenden Diagonalpunkt, der dem Punkt mit der ungeraden Quadratzahl gegenüber liegt.

Dem Quadrierungsergebnis der geraden Zahlen entsprechen im ersten Quadrat 4, im zweiten 16 Einzelquadrate.

2. Wenn man von der Zahl 1 an die folgenden Zahlen addiert, nach der letzten addierten Zahl dieselbe Rechnung wiederholt und die nächst höhere Zahl hinzufügt, so ist das Ergebnis beider Additionen das Quadrat der höheren Zahl. Als Beispiel mögen die Zahlen 2 und 3 dienen: 1+2 = 3; 1+2+3 = 6; 3+6 = 9 = 3².

Bezeichnet man die größere Zahl als a und das zu erwartende Ergebnis a² als x, nimmt die algebraische Rechnung folgenden Verlauf:

x= (a-1)/2*a + a/2*(a+1)

2x = a²-a + a²+a

2x = 2a²

x= a²

Ausgangsmodell für diese Regel sind die trinitarischen Zahlen 1 und 2, aus denen die erste Quadratzahl 4 hervorgeht: 1+(1+2) = 4.

3. Der Abstand der Quadratzahl 4 zur 1 beträgt 3. Danach rücken die ersten beiden Zahlen 1 und 2 um einen Zähler (2+3) vor, um durch Hinzufügung ihrer Summe 5 zur geraden Quadratzahl 4 die nächste ungerade Quadratzahl 9 zu erreichen: 4+5 = 9. Der Abstand zwischen 1 und 9 beträgt 3+5 = 8.

Die beiden nächsten Additionen sind 3+4 = 7 und 4+5 = 9. Der Zuwachs zum vorhergehenden Zahlenpaar 3+5 ist jeweils 4, zusammen 8. Der zweite Zahlenkranz wird also nach dem ersten um diesen Zuwachs von 8 erweitert: 1+8 =9; 9+(8+8) = 25. Eine Tabelle soll dies veranschaulichen:

QR Nr.	(1)	3	5	7	9
Qu. Z.	1	9	25	49	81
Abstand	–	3+5	7+9	11+13	15+17
Z.Kranz		8	16	24	32

4. Zur Vollständigkeit konzentrisch numerierter QR gehören die horizontalen und vertikalen Verbindungslinien. (Wie sie zustande kommen, sei hier offen gelassen.) Bezeichnet man die Achsenkreuz Nr. mit a, ergibt sich als Gesamtsumme der Punkte, Einzelquadrate und Linien:

a² + (a-1)² + 2a(a-1).

Das Ergebnis ist (2a-1)². Die Zahl der Punkte, Einzelquadrate und alle Elemente zusammen kann man an einer Quadratseite ablesen: Eine Seite aus 5 Punkten + 4 Linien ergibt 5² = 25 Punkte, 4² = 16 Einzelquadrate und (5+4)² = 81 Gesamtelemente.

III. Die trinitarische Bedeutung der Zuwachszahl 8

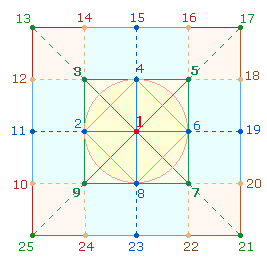
1. Wenn mit jedem Zahlenkranz 8 neue Zahlen hinzukommen, ist zu untersuchen, wo diese Zahlen im neuen QR Platz finden. Die zwischen den Eckpunkten liegenden Punkte des kleineren QR haben jeweils eine vertikale oder horizontale Verbindung zum größeren QR. Von den 4 Eckpunkten des kleineren QR gibt es 3 Fortsetzungen, eine diagonale, eine horizontale und eine vertikale. Die diagonale ist die axial gegebene, daher sind die beiden anderen Punkte die neu hinzukommenden Stellen:

2. 4*3 Winkelpunkte im Verhältnis 1:2 gehören also zusammen. Ihre Anknüpfungsstelle vom Eckpunkt des kleinere QR her ergibt somit das Verhältnis 1:(1:2) = 1:3 und zwar 4-mal. Daraus läßt sich die trinitarische Gleichung bilden: 1+3 = 4. Diese trifft im Quadrat viermal zu.

Die Multiplikationsformel (1+3)*4 kann auf vierfache Weise gebildet und als dreistellige Zahlen auf ihre Faktorenwerte (FW) überprüft werden:

			sm			sm	GS	FW	sm
Zahl	134	431	565	314	413	727	1292	40
FW	69	431	500	159	66	225	725	39
500:225 = 25*(20:9)							2017	79	2096
2096 = 16*131

Die Ergebnisse sind auf die Zahl 5 bzw. auf die Zuwachsformel ausgerichtet:

– Der gemeinsame Teiler 25 weist auf das 5*5 Quadrat hin, die Zahl 20 auf ein Achsenkreuz aus 4*5 Punkten je Achsenarm, die Zahl 9 auf 5+4 Punkte einer Achse.

– Die Primzahl 2017 läßt sich auf die vier Achsen eines 5*5 Quadrats beziehen: 4*5 = 20 Punkte, die sich bei einem Mittelpunkt um 3 auf 17 reduzieren.

– Das Endergebnis 16*131 ist beziehbar auf die 16 Punkte der Formel 4*(1+3) und auf das Verhältnis von 1:3 bzw. 3:1 Punkten einer Eckpunktformation, möglicherweise auch für die Unterscheidung der 5 Punkte einer Quadratseite: 1 Eckpunkte, 3 Mittelpunkte, 1 Eckpunkt. Letzteres kann als ein Prinzip des SATOR-Quadrats angesehen werden.

Erstellt:Januar 2008

index