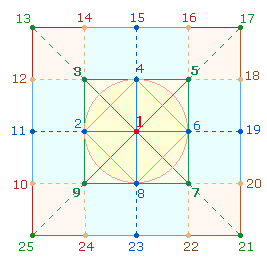
Das numerierte 5*5 Punkte Quadrat (4)
|
|
VII. Das Verhältnis der
linken zur rechten Seite
a) Die 4*3 Winkelpunkte
1.
Die komplementär gleichen Summen der vertikalen Eckpunkte
(13+25; 17+21) läßt es sinnvoll erscheinen, die Winkelpunkte der linken und
rechten Seite miteinander zu vergleichen. Die Zahlensumme (ZS) + Faktorensumme (FS) beider
Seiten sind:
|
|
li. |
re. |
|
|
ZS |
98 |
114 |
212 |
|
FS |
55 |
65 |
120 |
|
|
153 |
179 |
332 |
2. Die
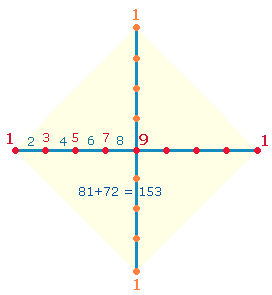
Gemeinsamkeit der beiden Summen besteht zunächst darin, daß sich die Zahl 153 aus 17*9 und 179 aus 17*9+(17+9)
zusammensetzt. Die Einzelziffern der Zahl 98 weisen auf
ein Achsenkreuz aus 9 Punkten + 8 Linien hin, während die Zahl 114 in der
Lesung 1+14 die Numerierung der 5 Punkte des AK2 darstellt. Die fortlaufende Addition
der Zahlen 1-17 – kreisförmig und konzentrisch von innen nach
außen – ergibt 153.
Nimmt man für
die Zahl 17 das Achsenkreuz AK5 an, das ja zum QR5 wird, bleiben bei der Numerierung
die Linien unberücksichtigt. Um sie für die Zahlen 153 und 179 einzubeziehen, bedarf es einer anderen
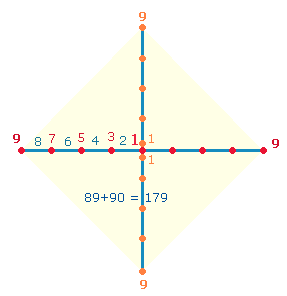
Numerierungsweise: Vom Mittelpunkt aus, dem man den Wert 1 gibt, numeriert man die 4 Achsenarme von 2-9, oder man benennt die 4 Randunkte mit 1 und rückt bis zum Mittelpunkt vor, der den Wert 9 erhält:
|
|
|
3.
Die Faktorenwerte (FW) von 153 und 179 sind 23+179 = 202 = 2*101 = FW 103. Die zwei FW zeigen die beiden Beziehungen der Eck- und Winkelpunkte:
Der Eckpunkt des QR3 bezieht sich direkt auf den Eckpunkt
des QR5, beide stehen den zwei Randpunkten gegenüber.
Andererseits besitzt der Eckpunkt des QR3 Verbindung
zu den 3 Winkelpunkten:
|
|
b) Die Winkelpunkte des QR5
+ Eckpunkte des QR3
1.
Die Hinzufügung der Eckpunktwerte des QR3 führen zu folgendem Ergebnis:
|
|
li. |
|
|
re. |
|
|
|
|
QR5 |
QR3 |
|
QR5 |
QR3 |
|
|
ZS |
98 |
12 |
110 |
114 |
12 |
126 |
|
FS |
55 |
9 |
64 |
65 |
12 |
77 |
|
|
|
|
174 |
|
|
203 |
|
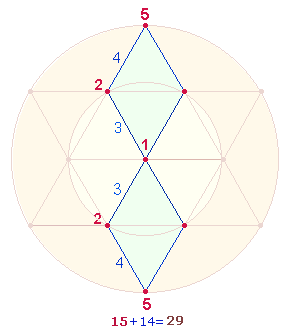
174:203 = 29*(6:7) |
||||||
Die Zahl 29 entsteht als Summe einer symmetrischen Numerierung von 9 Durchmesserelementen von 1-5. Sie ist charakteristisch für
die DM-Elemente der Doppelraute (DR):
|
|
2.
Die Verhältniszahlen 6:7 in
Verbindung mit 29 beziehen sich am ehesten auf die
Radialelemente des inneren und äußeren Kreises: 2*3 Elemente des
inneren Kreises bedeuten die Flächengröße 2, (2+2)+3 Elemente des äußeren Kreisrings und des inneren Kreises die Flächengröße 2+2+1 = 5. Rechnet man
für 29 jeweils die Flächengröße 3, ergibt sich das Flächenverhältnis 5:8.
Erstellt:Januar 2008