Bedeutung
der Zahl 154
I. Die
Umkehrzahlen 123/321
I. Die Umkehrzahlen 123/321
1. Die Zahl
154 ist eine Schlüsselzahl des trinitarischen Prinzips
und des Dezimalsystems, doch nicht leicht zu erklären. Sie tritt immer wieder
in bedeutenden Zusammenhängen auf. Als Ansatzpunkte des Verständnisses bieten
sich die Einzelziffern und das Produkt 11*14 an.
2. Bedeutender Bezugspunkt sind die
Umkehrzahlen 123
und 321. Deren Primzahlfaktoren sind 3*41 und 3*107. Die Addition der Faktoren 41+107 ergibt 148 = 4*37. Die Zahl 41 weist auf das Doppelrautenkreuz aus 21+20 Elementen hin, die Zahl 107 auf die Tetraktys mit 10 und das Hexagon mit 7 Punkten sowie auf 10 Linien + 7 Punkte der Doppelraute.
Durch Addition der zweimaligen
Faktoren 3 erhält man die FS 148+6 = 154.
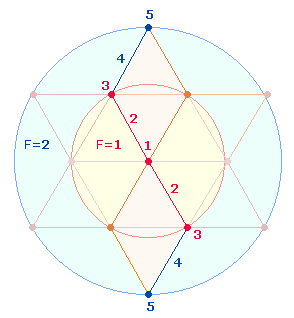
Auf sehr variable Weise bezieht sich die Zahl 154 auf den Tetraktysstern:
|
|
1.
Numeriert man die 9
DM-Elemente von 1-5 vom Mittelpunkt nach außen, ist
die Summe von 1-5 15, die restlichen 4 Zahlen ergeben 14. Die Zahl 154 kann man in 15+14 aufteilen.
Den 9 DM-Elementen des Tetraktyssterns
entsprechen 2*5
Radialelemente des Doppelkreises. Die Ziffern 154 verbinden so die ungerade Zahl der 9 DM-Elemente mit der geraden Zahl
der 10 Radialelemente.
2. Das Flächenverhältnis der beiden
konzentrischen Kreise des Tetraktyssterns ist 1:3, Kennzeichen des einen Gottes in drei Personen, das
Flächenverhältnis des inneren Kreises zum äußeren Kreisring 1:2. Die beiden Verhältnisse können durch 11 und 14 auf folgende Weise wiedergegeben
werden:
Die Zahl 11 bezieht sich auf die beiden
Kreise aus Mittelpunkt, zwei Kreisbögen und zwei Flächen, von denen die äußere Fläche nur den Kreisring von 2 Flächeneinheiten umfaßt. Diese
erste Zählung von 5
Elementen kennzeichnet das Flächenverhältns 1:2. Bei einer zweiten Zählung erhält auch der äußere Kreis
einen eigenen Mittelpunkt, was dem Flächenverhältnis 1:3 entspricht. Die Zahl 11 würde sich also auf 5+6 Elemente zweier konzentrischer Kreise beziehen.
Die Zahl 14 ist aufzuteilen in 7+7 Punkte für jeden Kreis des Tetraktyssterns. Das dadurch
repräsentierte Flächenverhältnis ist 1:3.
3.
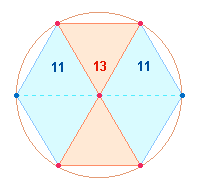
Im
Hexagon lassen sich zwei Arten von Doppeldreiecken unterscheiden: ein
sanduhrförmiges in der Mitte und zwei Rauten zu beiden Seiten:
|
|
Ein Dreieck besteht aus 7 Elementen, zwei aus 14. Die Raute hat eine gemeinsame
Mitte aus 3 Elementen. Die Doppelzählung
ergibt 14+11
= 25.
Dasselbe Verfahren für das
mittlere Doppeldreieck führt zur Addition 14+13 = 27. Durch Addition erhält man 25+27+25 = 77.
Erstellt: Februar 2007, September
2009, Januar 2011