Die Zahl 273
Die Zahl 273 soll anhand von geometrischen und numerischen Gesichtspunkten erklärt werden.
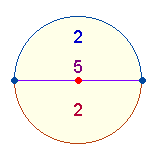
1. In der Aufteilung (2+7)+3 wird ein Kreis zweimal dargestellt: als zwei Kreishälften und als ganzer Kreis:
|
|
Durch die Kreisteilung sind Kreisbogen und Fläche doppelt zu zählen, zum Mittelpunkt kommen 2 Punkte und 2 Radialmaße hinzu. Die 5 Durchmesserelmente werden der zweiten Kreishälfte zugeordnet. Ein ganzer Kreis besteht aus den 3 Elementen Mittelpunkt, Kreisbogen und Fläche.
2. Die Zahl 273 entsteht aus dem Produkt 13*21. Die beiden Faktoren sind Fibonacci-Zahlen.
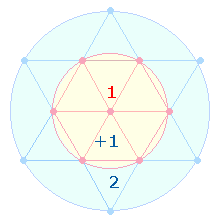
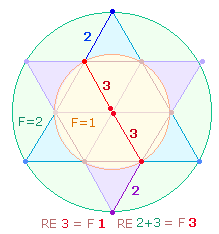
1. Durch Erweiterung des Hexagon entsteht der Tetraktysstern. Ein zweiter konzentrischer Kreis bewirkt zwei Kreisflächenverhältnisse 1:2 und 1:3:
|
|
Die Faktoren 21*13 enthalten die Einzelziffern der beiden Flächenverhältnisse.
Im Tetraktysstern sind drei Doppelrauten (DR) erkennbar. Eine DR besteht aus 21 Elementen, das hexagonale Doppeldreieck aus 13 Elementen. 13:21 Elemente geben daher das trinitarische Kreisflächenverhältnis 1:3 wieder.
2. Eine Tetraktysseite besteht aus 4 Punkten und 3 Linien, zusammen aus 12 Punkten und 9 Linien:
|
|
Der Faktorenwerte (FW) von 12 und 9 sind 7+6 = 13.
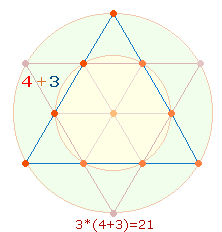
Das Hexagramm enthält zwei Tetraktys. Eine Tetraktys besteht aus 7 hexagonalen und 3 Eckpunkten. 273 kann daher gelesen werden als 2*(7+3) Punkte.
3. Auch die 21 Elemente der DR können in 12+9 aufgeteilt werden:
|
|
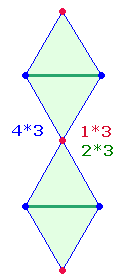
Der DR-Rahmen enthält 4*3 = 12 "Dachelemente", bestehend aus zwei Linien und einem Punkt dazwischen. Die übrigen Punkte bilden die Längsachse aus 3 Punkten, 2 Linien und 4 Flächen.
Jeder der 3 Schnittpunkte faßt 3 Punkte zusammen, d.h., die linke und rechte Zickzacklinie sowie die Längsachse bestehen aus je 9 Elementen. Da es im Tetraktysstern drei DR gibt, kann 273 verstanden werden als 27*3 = 81 Elemente. Die Einzelziffern der Zahl 81 geben die Zahl der Durchmesserelemente einer Zickzacklinie wieder.
4. Von den drei Einzelziffern gibt es 6 dreistellige Umkehrungen. Die Zahlensummen (ZS) und Faktorensummen (FS) sind:
|
3*79 |
82 |
319 |
|
|
723 |
3*241 |
244 |
967 |
|
372 |
2*2*3*31 |
38 |
410 |
|
273 |
3*7*13 |
23 |
296 |
|
327 |
3*109 |
112 |
439 |
|
732 |
2*2*3*61 |
68 |
800 |
|
2664 |
|
567 |
3231 |
|
2664 =
72*37; 567 =
21*27 |
|||
|
567:2664
= 9*(63:296) |
|||
|
3231
= 9*359 = FW 365 |
|||
Die Faktoren 21*27 weisen auf die 3*9 Durchmesserelemente einer DR hin, die durch drei Schnittpunkte auf 21 reduziert werden.
Die Aufteilung der Gesamt-ZS+FS in 32+31 zeigt die Konstitutivzahlen ihrer Summe 63 = 3*21 DR-Elemente an. Als Einzelziffern bedeuten 3:2 und 3:1 zwei Kreisflächenverhältnisse des äußeren Tetraktyskreises zum Erweiterungsring (3:2) und zum Hexagon (3:1).
Die Primzahl 359 weist auf 3+5 Radialelemente und 5+9 Durchmesserelemente hin, die jeweils das Kreisflächenverhältnis 1:3 wiedergeben:
|
|
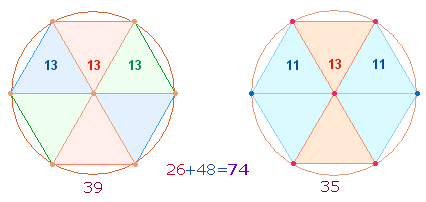
39 = 3*13 zeigt in seinen Einzelziffern die Punktestruktur der DR. Den Zahlen 39 und 35 entsprechen die Elemente von jeweils drei Doppeldreiecken, zweimal in Form von Rauten:
|
|
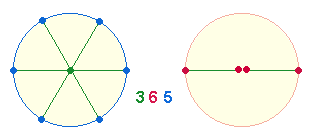
Der FW 365 gibt die Tage des Sonnenjahres wieder, als Einzelziffern 3*(6+5) gelesen den Doppelaspekt von Radialelementen und Durchmesserelementen der drei Hexagonachsen:
|
|
Die ZW+FW-Summe 296 = 8*37 = FW 43 der Zahl 273 enthält den Faktor 37 der ZS der 6 Umkehrungen. Die Primzahl 439 ist als 4*3+9 zu lesen, sie bezieht sich auf die 12 Dachelemente und 9 Längsachsenelemente.
Erstellt: Juni 2017