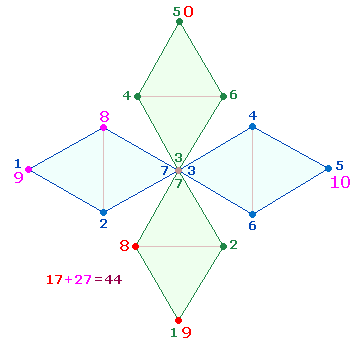
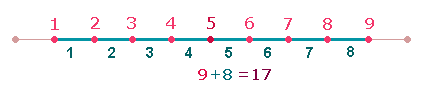Die trinitarische Bedeutung der Zahl 7
A. Bedeutung für das Dezimalsystem
I.
Einleitung
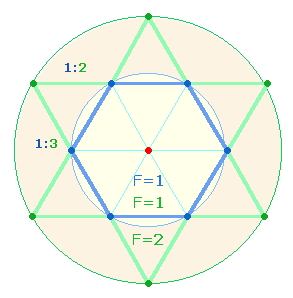
II. Die Verhältnisse 1:2 und 1:3
V. Ein rechnerischer Beweisgang
s.a. Das
trinitarische Prinzip 1 und 3
I.
Einleitung
1. Jede Zahlendeutung beruht auf mehr
oder weniger rationalen Grundlagen. Es gibt deren viele. Die Grundlage, die hier
gelten soll, ist eine ontologische. Ontologisch bedeutet erstens: im Sein des
Dreieinen Gottes selbst gegründet, zweitens Analogie zwischen Schöpfer und
Schöpfung. Demnach ist das Dezimalsystem Abbild des dreieinen Gottes und aus
geometrischen Modellen und weiteren mathematischen Prinzipien objektiv
erkennbar. Beide Bereiche habe ich unter Entwicklung des Dezimalsystems dargelegt.
2. Die Zahl 7 gilt als heilige Zahl. Im jüdisch-christlichen
Glauben ist sie zahlreich vertreten: 7 Schöpfungstage, siebenarmiger Leuchter, 7 Worte Jesu am Kreuz, 7 Sakramente, 7 Todsünden usw. Gewöhnlich wird
sie in 3+4 bzw. 4+3 aufgeteilt. Weitere Einteilungen
sind 2+5 und 1+6 mit Umkehrungen.
Ontologische Zahlenordnung
bedeutet auch, daß Einzelziffern ihre Bedeutung in Zusammensetzungen behalten
und in größeren Zusammenhängen entfalten und zu ihrem Ziel gelangen.
3. Für numerische Beweisgänge ist die
Einbeziehung der Faktorenwerte (FW) unerläßlich.
II. Die Verhältnisse 1:2 und 1:3
1.
Der
Einteilung der Zahl 7 in 3+4 liegt insbesondere das Verhältnis
1:2 und 1:3 im Hexagon und dem Tetraktysstern
zugrunde. Ersteres betrifft die Erweiterung des Hexagons zum Tetraktysstern:
|
|
Das Maß einer Segmentlinie wird symmetrisch um zwei weitere verlängert. Andererseits
stellen Hexagon und Tetraktys zwei unterschiedene Figuren dar,
sodaß auf eine Segmentlinie des Hexagon drei Maßeinheiten einer Tetraktysseite fallen.
Dieselbe doppelte Sicht gilt für
die beiden konzentrischen
Tetraktyskreise: Der Erweiterungsring hat die doppelte Fläche des Hexagons. Wenn
beide Kreise als selbständig betrachtet werden, ist das Flächenverhältnis
beider Kreise 1:3.
2.
Die
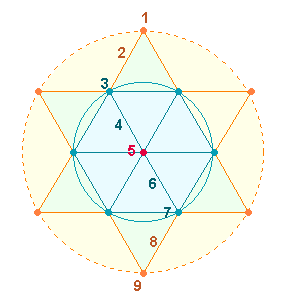
beiden trinitarischen Verhältnisse ergeben sich auch aus den Grundzahlen 1-9, die in den 9 DM-Elementen des Tetraktyssterns
ihr geometrisches Modell haben:
|
|
Nimmt man die Zahlen 1-5 als zusammengehörige Einheit an,
beträgt das Verhältnis der Summen 1-5 und 6-9 15*(1:2) und das Verhältnis des Teils zum
Ganzen 15*(1:3):
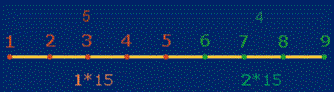
Dem Flächenverhältnis 1:3 der beiden konzentrischen Tetraktyskreise entsprechen 5:9 DM-Elemente.
3.
Welche
Beziehung haben die beiden Verhältnisse zur Einheit der drei göttlichen
Personen? Eigentlich sollte das Verhältnis 1:3 genügen.
Die Seinsrealität der
Dreifaltigkeit besteht aus zwei Aspekten, die in ihrer Absolutheit
zusammenfallen: dem des Werdens
und dem des Seins:
Einerseits geht die zweite und dritte Person aus der ersten hervor,
andererseits sind alle drei Personen im Wesen gleich und bilden darin eine
Einheit in vollkommener Gemeinschaft.
1. Nichts ist, was nicht geworden
ist. Das gilt auch für das Hexagon mit 7 und die Tetraktys mit 10 Punkten. Ein Entwicklungsprinzip ist offensichtlich das
Verhältnis zwischen Zahl und ihrem Faktorenwerte (FW), d.h. der Addition der Primfaktoren. Die Zahl 10 besteht aus 2*5, ihr FW ist also 7. Entwicklung erscheint so als
Fortschreiten von Addition zu Multiplikation.
Während nach üblichem Verfahren
Primfaktoren aus Zahlen ermittelt werden, kann man die Reihenfolge auch umdrehen:
Man legt zwei oder mehr Zahlen zugrunde, addiert sie zuerst, multipliziert sie
anschließend und stellt das Verhältnis zwischen Additions- und
Multiplikationsergebnis fest. (Der Faktor 1 soll unberücksichtigt bleiben.) Die Zahl 7 z.B. setzt sich aus 2+5 oder 2+2+3 zusammen. Addition und Multiplikation ergeben das FS:ZS-Verhältnis 7:10 und 7:12. Beide Zusammensetzungen bilden
das FS:ZS-Verhältnis 14:22 = 2*(7:11), das (interne) Differenzverhältnis zwischen FS und ZS ist 7:4. Die Einzeladditionen ergeben 7+10 = 17 und 7+12 = 19.
die FS 10 ergibt sich aus 5
verschiedene Zusammensetzungen von Faktoren, die
Multiplikationsergebnisse hierfür sind 21+25+30+32+36= 144.
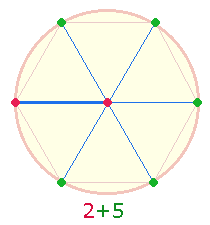
2.
Nach
den bisherigen Überlegungen sind die 7 Hexagonpunkte in 2+5 aufzuteilen. Tatsächlich genügt der Mittelpunkt und ein
Kreislinienpunkt, um die übrigen 5 Punkte festzulegen:
|
|
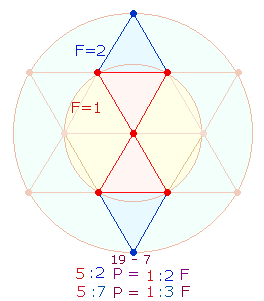
Ihre symmetrische Vollendung erhalten
die beiden Zahlen in der Doppelraute, die aus 5 hexagonalen und 2 Erweiterungspunkten besteht:
|
|
3.
Das
Multiplikationsergebnis schließt das Additionsergebnis ein, ähnlich zwei konzentrischen
Kreisen. Die 7 Punkte des Hexagons und 10 Punkte der Tetraktys können daher zu den Flächenverhältnissen der
beiden Tetraktyskreise in Beziehung gesetzt werden. 7+10 = 17 beinhaltet daher das Verhältnis 1:3, 7+3 = 10 das Verhältnis 1:2.
Ähnliches gilt für die
Doppelraute, wie aus vorstehender Grafik ersichtlich ist. Das Punkteverhältnis 5:7 hat eine Entsprechung in den 5 Durchmesserelementen des Hexagons
und den 7 Elementen einer Tetraktysseite.
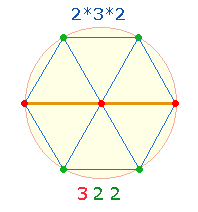
4.
Die
Zahlenverbindung 3+(2+2) ist
im Hexagon durch 3
Punkte der Mittelachse und 4
Punkte der Achsen zwei und drei gegeben:
|
|
Die multiplikative Erweiterung
kann in den 12
hexagonalen Linien (Maßeinheiten) gesehen werden, bestehend aus 3*2 und 2*3.
Im Zusammenhang damit ist eine 2+5 Kombination zu erwähnen, die
durch Kreisteilung zustande kommt: Eine Kreishälfte besteht aus den 2 Elementen von Kreisbogen- und Flächenhälfte sowie 5 Durchmesserelementen. Im
vollendeten Hexagon besteht eine Hälfte aus 10 Elementen: 5 Punkten, 7 Linien, 3 Dreiecken. (Das Kreisbogenelement
bleibt unberücksichtigt.)
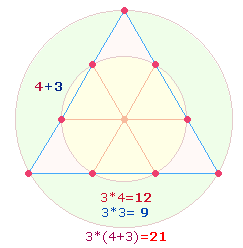
5.
Die
Kombination 4+3 beherrscht
den Tetraktysrahmen. Eine Tetraktysseite besteht aus 4 Punkten und 3 Linien, drei Tetraktysseiten aus 3*4 Punkten:
|
|
Die Addition 7+12 = 19 ist bereits im Zusammenhang mit
der Doppelraute genannt worden. In der Tetraktys ist die Zahl 19 durch 10 Punkte + 9 Rahmenlinien und durch 10 Punkte + 9 Dreiecksflächen vertreten. Eine
direkte Aufteilung von 7+12
findet nicht statt.
1.
Der
Multiplikation 2*5 = 10
entspricht die Addition 5+5 = 10.
Deren multiplikative Erweiterung ist 5*5 = 25. Das entsprechende FS:ZS-Verhältnis ist 5*(2:5) = 5*7.
Die Faktoren 5 und 7, bezogen auf die Punkte der DR, bedeuten das Flächenverhältnis 1:3.
Sowohl 5+5 als auch 5*5 sind im Tetraktysstern vertreten:
5+5 als Radialelemente des Tetraktyssterns und 25 als Anzahl der Hexagonelemente (7 P, 12 L, 6 F). Auch die 24 Erweiterungselemente + Mittelpunkt ergibt 25 sowie 13 Punkte +12 Dreiecksflächen des gesamten
Tetratyssterns.
Aus 25 Elementen besteht auch das 3*3 Punkte-Quadrat und die 25 Punkte des nächst größeren konzentrischen 5*5 Punkte-Quadrats, dessen zwei
Quadratrahmen in analoger Übereinstimmung mit den beiden konzentrischen
Tetraktyskreisen steht.
2.
Die
Konstituenten der Zahl 25
sind 12+13, zweistellige Zusammensetzungen
der beiden trinitarischen Verhältnisse 1:2 und 1:3. Der Zahl 25 kommt somit hohe trinitarische
Bedeutung zu. Die 9+16
Punkte im 5*5 Punkte-Quadrat entsprechen dem
Satz des Pythagoras, gemäß dem in einem rechtwinkligen Dreieck die
Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des
Hypothenusenquadrats sind. Die Verdoppelung des rechtwinkligen Dreiecks ergibt
ein Rechteck aus 3*4 Einheiten. Quadrat und Rechteck
veranschaulichen so in besonderer Weise das Verhältnis von Addition und
Multiplikation (hier 7+12 = 19).
Das SATOR-Quadrat hat das 5*5 Punkte-Quadrat zur
Grundlage.
3.
Die
Zahl 10 ist nun einmal als multiplikative Erweiterung und einmal
als Addition zustande gekommen. Zusammen mit den begleitenden Werten erhält man
folgendes Ergebnis:
|
|
2|5 |
5|5 |
sm |
|
Add. =
ZS |
7 |
10 |
17 |
|
Mult.= FS |
10 |
25 |
35 |
|
sm |
17 |
35 |
52 |
Das Endergebnis 52 ist die Umkehrung von 25, der unteren Konstitutivzahl von 52. Ein ähnlicher Fall kommt nur
noch bei 37+36 = 73 vor. Die Addition beider Umkehrzahlen ist 125 = 5*25 = 5³.
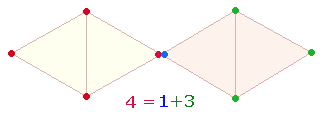
Die Faktoren von 52 sind 4*13 und stellen in ihren
Einzelziffern die Gleichung 4 = 1+3 dar, unter anderem zu beziehen auf 2*4 Punkte der Doppelraute (DR) bei einem zusätzlichen
Mittelpunkt:
|
|
Aus 13 Elementen besteht das hexagonale Doppeldreieck innerhalb der DR, die sich bei
der Oktaederbildung aus 2 DR vervierfacht.
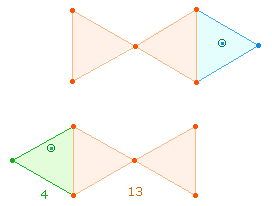
Aus 13+4 = 17 Elementen schließlich besteht
eine erweiterte (fischförmige) geometrische Figur:
|
|
Die FS 17 der Zahl 52 umfaßt Addition + Multiplikation der Ausgangszahlen 2 und 5, die auch die Einzelziffern von 52 bilden.
V. Ein rechnerischer Beweisgang
1. Der folgende Beweisgang soll am
Ende erneut zu den Verhältnissen 1:2 und 1:3 führen.
Ausgangspunkt sind die zusammengesetzten
Zahlen 12 und 13 und ihre Umkehrungen. In einem
zweiten Rechengang wird 12 mit
31 verbunden und deren Umkehrungen
gebildet. Von jeder ZS und FS werden die FW gebildet. Die ZS und FS mit ihren FW werden schließlich getrennt
addiert:
|
|
|
|
sm |
FW |
sm |
|
|
sm |
FW |
sm |
GS |
|
Zahl |
12 |
13 |
25 |
10 |
35 |
21 |
31 |
52 |
17 |
69 |
104 |
|
FW |
7 |
13 |
20 |
9 |
29 |
10 |
31 |
41 |
41 |
82 |
111 |
|
Zahl |
12 |
31 |
43 |
43 |
86 |
21 |
13 |
34 |
19 |
53 |
139 |
|
FW |
7 |
31 |
38 |
21 |
59 |
10 |
13 |
23 |
23 |
46 |
105 |
|
104+139 = 243;
111+105 = 216 |
|||||||||||
2. Die beiden Summen 216 und 243 sind durch 27 teilbar, ihr Verhältnis beträgt (8:9)*27 = 17*27.
Die
Zahlen 8 und 9 sind konzentrische
Komplementärzahlen zu 2 und 1. In Potenzschreibung sind beide
Zahlen Umkehrungen: 2³ und
3². Ihr FS:ZS-Verhältnis ist 6:8 = 2*(3:4) und 6:9 = 3*(2:3). Die Klammerzahlen 3+2 = 5 und 4+3
= 7 sind Additivfaktoren und zugleich
Konstituenten der Zahl 12. Das
interne Differenzverhältnis der Zahlen 8 und 9
ist 3:1 und 2:1.
3.
Die
Produktzahlen 17 und 27 haben mit der Oktaederbildung als
Vollendung des Dezimalsystems zu tun. Eine DR besteht aus 7 Punkten wie das Hexagon. Es geht um das Problem, wie man
von 7 zu 10 gelangt, was in der Tetraktys bereits verwirklicht ist.
Es geschieht in der schleifenförmigen Numerierung der Punkte und Vereinigung
der beiden Endpunkte, wodurch eine 10. Position besetzt werden kann, einmal durch den
Ausgangspunkt 0 und
einmal mit dem Zielpunkt 10.
Die über die doppelte Numerierungssumme 28 der Zahlen 1-7 hinausgehenden Summen sind so 17+27 = 44, das Verhältnis beider Summen 56:44 = 4*(14:11) = 100:
|
|
4.
Das
FS:ZS-Verhältnis 8:9 kann folgendermaßen gedeutet
werden:
9 Punkte begrenzen 8 Maßeinheiten:
|
|
Dasselbe Verhältnis von Punkten
und Maßeinheiten kann durch ein Achsenkreuz AK3 wiedergegeben werden.
|
|
Erstellt: Dezember 2010