Die
trinitarische Bedeutung der Zahl 7
B.
Zusammensetzungen, Dreieck, Raute
I. Einleitung
II. Zusammensetzungen der Zahl 7
III.Bedeutung des Dreiecks und der Raute
I.
Einleitung
Die Einteilung in A. und B. ist erst nachträglich erfolgt.
Wenn man schneller zum Ziel einer Gesamtaussage gelangen möchte, geht man
bisweilen unversehens von Gegebenheiten aus, die zuvor erklärt werden müßten.
Es geht also in diesem zweiten Teil um notwendige Nachträge und Ergänzungen.
Geometrische Modelle und das Zusammenwirken von Addition und Multiplikation sind dabei wiederum verläßliche
Instrumente objektiver Erkenntnis.
II. Zusammensetzungen der Zahl 7
1.
In Anknüpfung an das Ende des ersten Teils möchte ich mit einem weiteren
Rechengang beginnen, und zwar mit drei Zusammensetzungen der Zahl 7: 1+6, 2+5, 3+4. Von ihren Additionen und
Multiplikationen sind die Faktorenwerte (4Werte) zu ermitteln und hinzuzufügen:
|
|
Add. |
Mult. |
sm |
FW1 |
FW2 |
sm |
GS |
|
1|6 |
7 |
6 |
13 |
7 |
5 |
12 |
25 |
|
2|5 |
7 |
10 |
17 |
7 |
7 |
14 |
31 |
|
3|4 |
7 |
12 |
19 |
7 |
7 |
14 |
33 |
|
|
21 |
28 |
49 |
21 |
19 |
40 |
89 |
Die Multiplikation erbringt eine 7-er Einheit mehr als die Addition,
das Verhältnis ist 7*(3:4).
Die Quadratzahl von 7 ist auch
die Summe der Elemente des Tetraktyssterns.
2.
Die Gesamtsumme und Primzahl 89 mit ihren Teilsummen 49 und 40 wirft Licht auf einen weiteren
bedeutsamen Zusammenhang: Die Zahlen 8 und 9
haben, wie im am Ende des ersten Teil dargelegt, die FW 6+6 und das interne FW:ZW-Verhältnis 1:3 und 1:2. Ihre ZS+FS
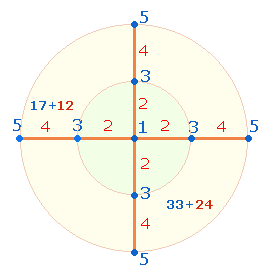
ist 17+12 = 29. Die Gesamtzahl wie ihre
Aufteilung ist als symmetrische Numerierung einer Achse darstellbar:
|
|
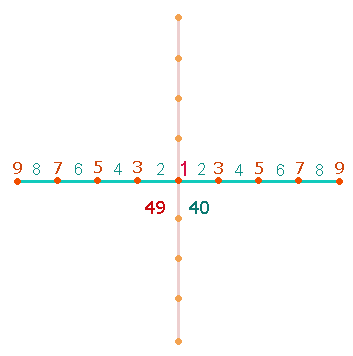
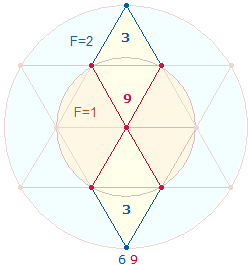
Wenn man die Achse um jeweils vier
Elemente erweitert und von 6-9
numeriert, erhält man 29+60 = 89:
|
|
Die Numerierungssummen der Punkte
und Linien betragen 49 und
40. Die Summen 29 und 89 lassen sich verbinden, indem man
einmal nur die Punkte und einmal Punkte + Linien numeriert.
3.
Die Zusammensetzung 1+6 führt zu den trinitarischen Verhältnissen 13+12 als zweistellige Zahlen und dem
Ergebnis 25,
das die zweite Zusammensetzung 2+5
wiedergibt. Die beiden Zusammensetzungen können als Entwicklung von den 1+6 hexagonalen Punkten zu den 5+2 Punkten der Doppelraute (DR) betrachtet werden. Letztere
erklärt die Werte 21 und 28 sowie die Beziehung der Zahl 7 zu 8 und 9: Die DR besteht aus 21 Elementen, aus 4 Dreiecksflächen und 7 Punkten, und 2+8 Linien, also die Faktoren und
Einzelziffern der Zahl 28. Die
Zahlen 8 und 9 kommen zur 7 hinzu durch schleifenförmige
Numerierung.
Aus 25 Elementen besteht sowohl das
Hexagon als auch das 3*3
Punkte-Quadrat. In beiden geometrischen Figuren sind die Zahlen 13+12 aufteilbar, im 5*5 Punkte-Quadrat wechseln der Reihe
nach ungerade und gerade Zahlen ab, wie dies für das SATOR-Quadrat relevant ist.
III. Die Bedeutung des Dreiecks und der Raute
1.
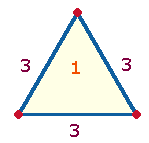
Das Dreieck gilt seit jeher als zentrales Symbol der
Dreifaltigkeit. Es wird jedoch, soweit ersichtlich, nicht mit der Zahl 7 in Verbindung gebracht, obwohl es
aus 7 Elementen besteht: 3 Punkten, 3 Linien und der umschlossenen
Fläche. Die Zahl 7 erhöht sich auf 10, wenn man jede Seite als ein
Streckenmaß betrachtet, das durch 2 Punkte begrenzt wird. Auf diese Weise
enthält das Dreieck bereits die Erweiterung der 7 hexagonalen Punkte zu den 10 Punkten der Tetraktys in sich:
|
|
Auch die zwei trinitarischen
Verhältnisse sind erkennbar: dreimal 2:1/1:2 und zweimal 3:1, drei Punkte/Linien zur Fläche. Das Verhältnis 4:3 läßt sich bilden, wenn man Punkte
und Fläche den drei Linien gegenüberstellt.
2.
Die trinitarischen Flächenverhältnisse 1:2 und 1:3 der beiden Tetraktyskreise sind nicht denkbar ohne das gleichseitige Dreieck. Denn der Tetraktysstern entsteht, indem jedes der 6 hexagonale Dreiecke ein
spiegelsymmetrisches Umkehrdreieck erhält und ein zweiter Kreisbogen um die 6 äußeren Punkte den Abschluß der
Entwicklung bildet.
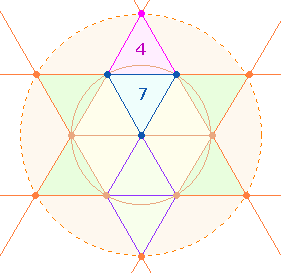
Je zwei vom Mittelpunkt aus nach
außen verlaufende Dreiecke bilden nun eine Rautenfigur. Die bestehende
Siebenzahl der Dreieckelemente wird durch das Umkehrdreieck um 4 Elemente erhöht:
|
|
Insofern die zwei Tetraktys des
Sechsecksterns aus 2*37 = 74
Elementen besteht, sind bereits in einer Raute die beiden ineinander
verschränkten Tetraktysfiguren vorgeprägt.
Das Umkehrverhältnis 4:7 entsteht, wenn man die 4 Punkte der Raute den 7 übrigen Elementen
gegenüberstellt.
3.
Indem man unterscheidet zwischen den Rautenelementen, die
dem Hexagon und denen, die der Erweiterung angehören, lassen sich Verhältnisse
parallel zu den trinitarischen Flächenverhältnissen bilden:
– 3:1 Punkte bedeuten das Flächenverhältnis 1:2 und 3:(3+1) = 3:4 Punkte das Flächenverhältnis 1:3.
–
7:4 Elemente bedeuten das
Flächenverhältnis 1:2 und 7:(7+4) = 7:11 Elemente das Flächenverhältnis 1:3.
4.
Die Ausgangsparallelen für die beiden Flächenverhältnisse
sind die Durchmesserelemente (DM) und Radialelemente des Tetraktyssterns. Für das Flächenverhältnis 1:2 z.B. lautet das Verhältnis der DM-Elemente 5:4 und der Radialelemente 3:2. Die Rolle der DM-Elemente
übernimmt das (sanduhrförmige) Doppeldreieck, die der Radialelemente die Raute. Die entsprechenden Verhältnisse
hierzu sind 7:4
und 13:8.
Das Doppeldreieck aus 13 Elementen steht so für 1 Flächeneinheit, die beiden Rauten aus 11 Elementen für jeweils 3 Flächeneinheiten. Den 7 Doppelrautenpunkten 3+1+3 entsprechen also ebensolche Flächeneinheiten.
Zusammengesetzt ergeben sich aus
der Zahl der Elemente und der Flächeneinheiten die dreistelligen Umkehrzahlen 113 und 311.
Nun gibt es im 4-stelligen Bereich zwei einzigartige Umkehrzahlen, deren
Faktoren wiederum Umkehrungen sind:
1469 = 13*113, 9641 = 31*311.
Die Summe der Faktoren ist 126+342 = 468 = 36*13, das Verhältnis 18*(7:19). Folgende drei Modelle dürften
damit in Zusammenhang stehen:
– Die Summen der
Zahlen von 1-4
und 6-9 sind 10 und 30 = 10*(1:3).
–
Der Doppelrautenrahmen besteht aus 9 Elementen des hexagonalen Anteils
und aus 6 Elementen der Erweiterung:
|
|
Das Verhältnis 7:19 deutet auf eine Analogbildung der 7 DR-Punkte im Verhältnis zu den
Kreisflächen hin: 5:2
Punkte bedeuten das Verhältnis 1:2, 5:7 Punkte das Verhältnis 1:3. Durch Addition erhält man 3+4 = 7 und 7+12 = 19.
–
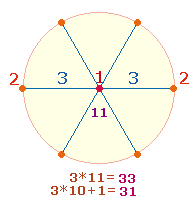
Wenn man die Umkehrzahlen 113 und 311 multiplikativ als 11*3 und 3*11 interpretiert, sind sie auf die
drei Hexagonachsen beziehbar, von denen jede auf zwei verschiedene Weise zur
Summe 11 gelangt: einmal als Doppelaspekt von 5 DM- und 6
Radialelementen und einmal als Numerierungssumme:
|
|
Wenn man den
Mittelpunkt nur einmal zählt, reduziert sich die Numerierungssumme auf 31, ebenso die 3*5 = 15 Achsenelemente auf 13. Auf diese Weise sind die
Umkehrfaktoren 13 und 31 erklärbar.
Die Zahlen 14 und 69 sind als Einzelziffern zu
verstehen, als 1+4
Elemente einer einzelnen Achse und als 6 Linien + 9
Punkte des Hexagons.
Erstellt: Dezember 2010