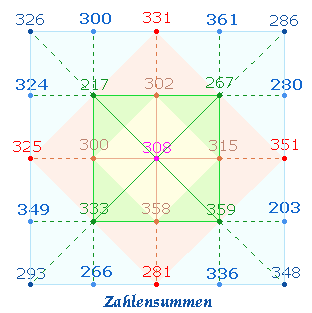
CATULL: CARMINA 5
und 7
B. Das C5C7-Quadrat nach dem Muster des
Palindroms 1-25
I. Einleitung
II. Die Zahlen 17 im
c5c7-Quadrat
III. Zweimal 17 und 18 im c5c7-Quadrat
IV. 5 spiegelsymmetrische Zahlengruppen
I. Einleitung
In
diesem Teil geht es um die Achsenkreuzzahlen 17 und 18,
ursächlich für die Buchstaben RS im Wort ROTAS des SATOR-Quadrats (SQ). Die Zahl 18
zeigt sich in der ZS+FS
sowohl der horizontalen als auch der vertikalen Achse, die Zahl 17 in den 4*3
Winkelpunkten des äußeren Quadratrahmens und den 8 Eckpunkten der beiden
Quadratrahmen.
Es ist zunächst auf das Zuwachsprinzip konzentrischer Quadratrahmen
einzugehen und darzulegen, was die Zahlen 5
und 7 mit der Zahl 17
zu tun haben.
II. Die Zahlen 17 im c5c7-Quadrat
|
|
|
|
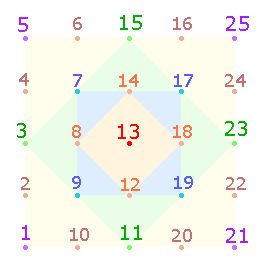
1. Die im linken Quadrat
eingezeichneten Linien lassen erkennen, daß die Eckpunkte des inneren Quadrats
Schnittpunkte von drei Linien sind, deren Fortsetzung zu drei weiteren Punkten
des nächst größeren Quadratrahmens führen. Jeweils drei dieser Punkte seien Winkelpunkte genannt, jeweils zwei
einem diagonalen Eckpunkt benachbarte als Zuwachspunkte, Flankierpunkte oder Randpunkte bezeichnet. Jeder
Quadratrahmen vermehrt die Punktezahl um eben diese 4*2 = 8 Zuwachspunkte
gegenüber dem nächst kleineren. Das 5*5 Punkte-Quadrat ist das erste, in dem diese
Zuwachspunkte auftreten, weshalb ihnen eine grundlegende Bedeutung zukommt. Die
Anzahl der Punkte der ersten vier Quadrate ist demnach 1+8 = 9, 9+(8+8) = 25, 25+3*8 = 49, 49+4*8 = 81.
2. In Bezug auf die
Eckpunkte lautet die Zuwachsformel von sich konzentrisch erweiternden Quadraten
(1+3)*4, (3+1)*4, 4*(1+3) oder 4*(3+1). Der erste Ausdruck
ist als dreistellige Zahl 134 = 2*67 die Zahlensumme (ZS) der 8 Eckpunkte des SATOR-Quadrats (SQ): 2*SRPR. (Weitere Ergebnisse zu den 4 Ausdrücken
siehe Das 5*5 Punkte-Quadrat)
3. Zwei Eckpunkte des inneren
und äußeren Quadrats am Ende jeder Diagonalachse bilden mit den beiden
Zuwachspunkten ein Quadrat. Die 4 Punkte können einander verschieden zugeordnet
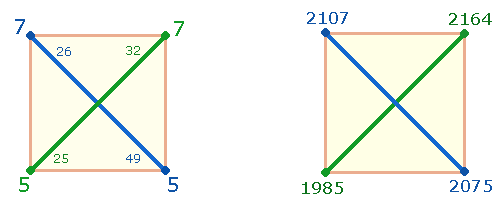
werden: in den Verhältnissen 1:3, 1:2 und 2:2. Die komplementäre Quadratnumerierung ergibt für die 8 Eckpunkte
und 8 Zuwachspunkte als Faktorensummen (FS) die zwei Umkehrzahlen 75 und 57:
|
|
Es dürfte keinem Zweifel
unterliegen, daß Catull die spiegelbildliche Quadratnumerierung kannte. Die
Summen der Eckpunkte enthalten die Einzelziffern der beiden Umkehrsummen als
Quadrate. Die FS 49 ist selbst eine Quadratzahl:
|
|
|
FW |
|
2107 |
7*7*43 |
57 |
|
2075 |
5*5*83 |
93 |
|
4182 |
6*17*41 |
63 |
Der
Faktor 43 der Zahl 2107 kennzeichnet die 4*3 Winkelpunkte des
äußeren Quadratrahmens, umfaßt durch 7*7 = 49 die FS der inneren Eckpunkte (der
Quadratnumerierung) und durch den FW 57 die FS der 8 Zuwachspunkte.
Der Faktor
41 bezieht sich
hauptsächlich auf die Summe der 25 Punkte und 16 Einzelquadrate.
4. Die FS und ZS der 12 Winkelpunkte sind im ersten
Teil behandelt worden. Die Summen 2584:3672 bilden das Verhältnis 8*17*(19:27) = 136*46 = 272*23.
Die
beiden durch 17 teilbaren Gesamtsummen sind 6256+4182 = 10438. Sie bilden das Verhältnis 34*(184:123) = 34*307 = FW 326. Die Zahl 326, aufgefaßt als 3*26, bezieht sich auf
drei Oktaeder, die durch 3*2 Doppelrauten gebildet werden können. Ihr liegt die zweimalige
Primzahl 163 zugrunde, Umkehrung zu 136. Beide Zahlen zeigen
in ihren Einzelziffern die Verteilung
der Tetraktyspunkte.
III. Zweimal 17 und 18 im
c5c7-Quadrat
1. Die ZS+FS der horizontalen und
vertikalen Achse sind:
|
|
ZS |
FS |
sm |
FW |
|
horiz. |
1599 |
1119 |
2718 |
159 |
|
vert. |
1580 |
1066 |
2646 |
25 |
|
sm |
3179 |
2185 |
5364 |
184 |
|
FW |
45 |
47 |
92 |
92*(1:2) |
|
2718:2646=18*(151:147)=36*149 |
||||
Das
Produkt 36*149 der Gesamtsumme läßt
sich beziehen auf zwei Tetraktysrahmen zu jeweils 18 Elementen und die 9 fortschreitend
addierten Dreiecke der drei Tetraktysstufen 1+4+9.
2. Die FS 92 = 4*23 bezieht sich auf die
vier Quadratseiten mit je 2 Eckpunkten und 3 dazwischen liegenden Punkten. Die Gesamtsumme 276 ist die Summe der
Zahlen 1-23. Durch 4 geteilt, ergibt sich,
den äußeren Quadratrahmen umlaufend, viermal der ZW 69 für SATOR ROTAS.
Es fällt
nicht schwer anzunehmen, daß die Produktzahl 34 und 36 = 2*(17+18) auf die Buchstaben R und S abzielen, die im SQ jeweils zweimal
vorkommen.
IV. 5 spiegelsymmetrische
Zahlengruppen
1. Die 12 Zahlenpaare der
spiegelsymmetrischen Numerierung können unterteilt werden in 4*2 und 1*4 Paare:
|
|
Die
Unterteilung folgt dem Aufbau des 5*5 Punkte Quadrats aus 1. Mittelpunkt, 2. kleinem
Rautenquadrat, 3. innerem Quadratrahmen, 4. äußeres Rautenquadrat, 5. Eckpunkten und 6. Zuwachspunkten des
äußeren Quadratrahmens.
2. Von den zu einer
Gruppe gehörigen Zahlen kann man die ZS und FS – getrennt und zusammen – und deren FW bestimmen. Von der
Einzelzahl 13 des Mittelpunktes
kann man lediglich den FW 13 angeben. Die Ergebnisse der folgenden Tabelle sollen nicht weiter
ausgewertet werden, sondern als Modell der Catullschen Konzeption vorgeschaltet
werden:
|
Gr. |
ZS |
FS |
FW1 |
FW2 |
ZS/FS |
FW |
GS |
|
1 |
13 |
13 |
– |
– |
26 |
15 |
|
|
2 |
52 |
30 |
17 |
10 |
82 |
43 |
|
|
3 |
52 |
49 |
17 |
14 |
101 |
101 |
|
|
4 |
52 |
45 |
17 |
11 |
97 |
97 |
|
|
5 |
52 |
26 |
17 |
15 |
78 |
18 |
|
|
6 |
104 |
57 |
19 |
22 |
161 |
30 |
|
|
|
325 |
220 |
87 |
72 |
545 |
304 |
1553 |
Von
Interesse ist die die Gesamtsumme und Primzahl 1553, insofern der Zahl 15 ihre Faktoren 5 und 3 folgen. Ovid hat für
seine aus 15 Büchern bestehende
Metamorphosen für die 4 Einleitungsverse die ZS 1553 gewählt.
3. Für die Catullschen
Werte seien die drei relevanten Grafiken wiederholt:
|
|
|
|
|
Gr. |
ZS |
FS |
FW1 |
FW2 |
sm |
FW |
ZS/FS |
Fkt. |
FW |
|
1 |
308 |
209 |
22 |
30 |
569 |
569 |
517 |
47*11 |
58 |
|
2 |
1275 |
908 |
30 |
231 |
2444 |
64 |
2183 |
37*59 |
96 |
|
3 |
1176 |
899 |
23 |
60 |
2158 |
98 |
2075 |
83*25 |
93 |
|
4 |
1288 |
859 |
36 |
859 |
3042 |
34 |
2147 |
19*113 |
132 |
|
5 |
1253 |
854 |
186 |
70 |
2363 |
156 |
2107 |
49*43 |
57 |
|
6 |
2419 |
1730 |
100 |
180 |
4429 |
146 |
4149 |
9*461 |
467 |
|
|
7719 |
5459 |
397 |
1430 |
15005 |
1097 |
|
|
903 |
|
|
|
|
1827 |
1827:903 = 21*(43:13) >76 |
|||||
Erstellt: Oktober 2009