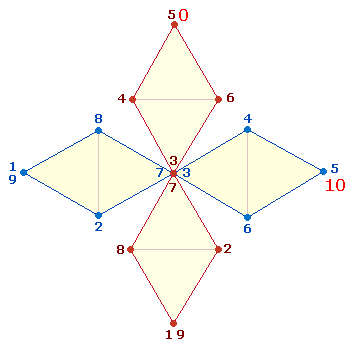
zu Carmen 5
CATULL: CARMEN 5 u. 7
Anmerkung (Mai 2023): Einiges der Nummern
II. und III. erscheint mir heute nicht mehr so relevant. Eine komplette
Überarbeitung ist nicht möglich. Ich füge neu einen Aspekt unter IV. hinzu.
A. Zahlen- und
Faktorensummen; Zahlenpalindrom 1-25
I. Zahlen- und
Faktorensummen
II. Die Zahlen 1-25 als komplementäres Palindrom
III. Zahlenverhältnisse im komplementären Palindrom
IV. Die 25 Werte von c 5 und 7 im 5*5 Quadrat
B. Parallelen zwischen Palindrom 1-25
und c5c7-Quadrat
C. Das Muster NET OPERA SATOR im
c5c7-Quadrat
I.
Zahlen- und Faktorensummen
Abkürzungen:
ZW (Zahlenwerte), FW (Faktorenwert), ZS (Zahlensumme), FS (Faktorensumme)
1.
Eine interpretatorische Behandlung des Carmen 7 ist mir zeitlich nicht möglich.
Einfacher ist die Ermittlung seiner ZS+FS, die, wie zu vermuten ist, mit den Werten seines
Parallelgedichts Carmen 5
zusammenstimmen. Die ZS+FS beider
Gedichte liefern folgende Ergebnisse:
|
|
c.5 |
c.7 |
sm |
Fkt. |
FW |
|
ZS |
3980 |
3739 |
7719 |
3* 31*
83 |
117 |
|
FW |
2796 |
2663 |
5459 |
53*103 |
156 |
|
sm |
6776 |
6402 |
13178 |
2*11*599 |
273 |
|
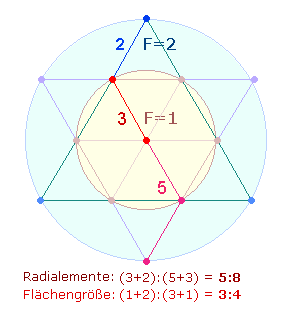
117:156 = 13*(9:12)
= 273 = 13*21 |
|||||
|
6776:6402 = 22*(308:291) = 2*11*599>612 |
|||||
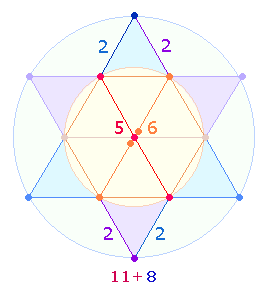
Der Faktor 31 der ZS entspricht dem ZW von BASIA. Der gemeinsame Teiler 13 bezieht sich auf die 13 Punkte des Tetraktyssterns, die
Verhältniszahlen 9 und 12 auf die 3*(3+4) Linien und Punkte des Tetraktysrahmens:
|
|
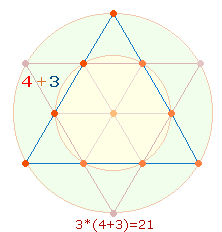
Das Produkt 13*21 enthält in der Addition seiner
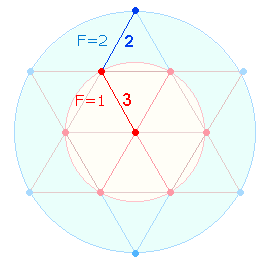
Einzelziffern die trinitarischen Zahlen 4+3. und ist auf die Doppelraute (DR) anwendbar: Aus 13 Elementen besteht das hexagonale
Doppeldreieck, aus 21
Elementen die Doppelraute. Sie geben das Verhältnis 1:3 der beiden
konzentrischen Kreise wieder.
Die ZS+FS der beiden Gedichte
sind jeweils durch 22 teilbar. Die Differenz ist 22*17 = 374. Die Zahl 22 steht für zwei Rauten aus je 11 Elementen, aber auch für das
genannte Flächenverhältnis 1:3, indem der hexagonale Kreis
zweimal mit jeweils einer Flächeneinheit und der äußere Kreisring einmal mit
zwei Flächeneinheiten vertreten ist.
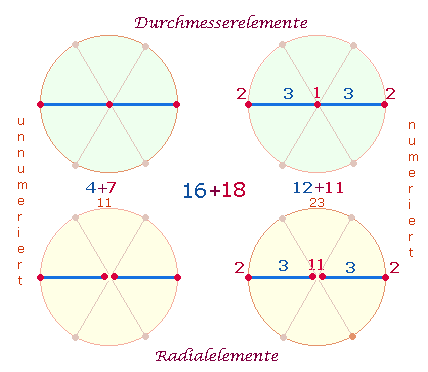
Die Primzahl 599, aufgeteilt in (5+9)+9, bezieht sich auf die Durchmesserelemente der beiden konzentrischen Kreise;
sie geben die Flächeneinheiten (1+3)+3 = 4+3 wieder.
2.
Auch die Addition der Buchstabenzahlen 358+324 = 682 von c 5 und c 7 ist durch 31 teilbar: Das Produkt 22*31 zeigt das Verhältnis von
Radialelementen zur entsprechenden Flächengröße an: 2:1
Flächeneinheiten des äußeren Kreisrings zum inneren Kreis:
|
|
II. Die Zahlen 1-25 als komplementäres Palindrom
1.
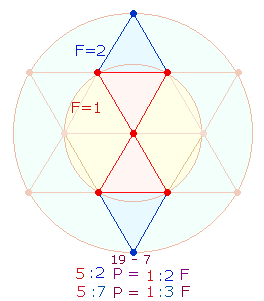
Die 13+12 Zeilen der Gedichte 5 und 7
entsprechen den Flächenverhältnissen 1:3 und
1:2 der beiden konzentrischen Kreise. Wenn nun der 13. Vers als einziger der 25 eine durch 11 teilbare ZS und FS aufweist (28*11, 19*11), ist an ein geometrisches Modell zu denken,
dessen 13. Element die Symmetriemitte
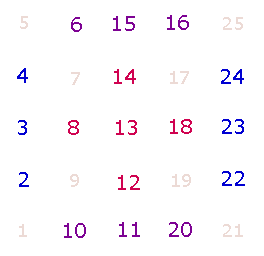
darstellt. Das ist am klarsten bei einem 5*5 Punkte Quadrat (oder 5*5 Quadratfeldern) der Fall, wenn man die 25 Punkte numeriert. Es wird zu
untersuchen sein, ob sich klare Konstruktionslinien zeigen. Wenn Catull die 25 Verse nach dem Vorbild des SATOR-Quadrats anordnete, liegt die Vermutung nahe,
daß er es als komplementäres Palindrom verstand.
2.
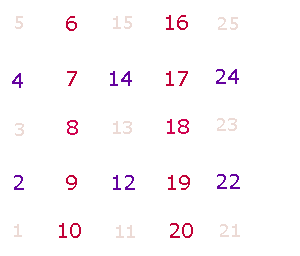
Entsprechend römischer Gewohnheit, Zahlenreihen von unten
nach oben zu schreiben, beginnt das SQ links unten:
|
|
|
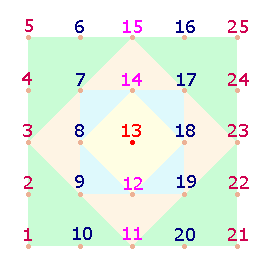
In einem Quadrat besitzt jeder
Punkt oder (jedes quadratisches Feld) eine spiegelbildliche Gegenposition. Bei
fortlaufender Numerierung von 1 bis n beträgt die Summe zweier symmetrischer Positionen stets n+1, im 5*5-Punkte-Quadrat also 26. In der rechten Grafik verläuft
die Numerierung der folgenden Zeile jeweils in Gegenrichtung zur vorherigen.
Die spiegelsymmetrische Summe 26
ist zwar auch gegeben, wenn jede Zeile von der gleichen Seite aus beginnt, wenn
also neben der 1 die
Zahl 6 statt 10 steht. Letzterem Verlauf stehen
jedoch zwei Umstände entgegen: Erstens, die spiegelsymmetrische Wortfügung NET OPERA SATOR verlangt nach beiden Seiten des Quadrats einen
spiegelsymmetrischen Verlauf. Zweitens, Catull liefert durch Einbeziehung der
Quadratnumerierung in seine geniale Zahlenkonstruktion einen eindeutigen
Beweis dafür,
daß eben 10 und nicht 6 neben der 1 stehen muß.
3.
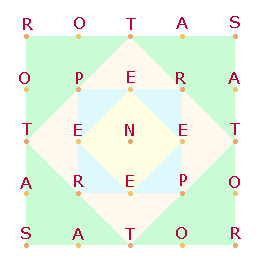
Im SQ
sind die spiegelbildlichen Positionen durch gleiche Buchstaben besetzt. Der
Aspekt der komplementäre Zahlenanordnung als Modell für das SQ führt zu einer wichtigen
Schlußfolgerung hinsichtlich der Art und Weise, wie es zu lesen ist.
Üblicherweise werden die 5
Wörter jeweils von links nach rechts gelesen:
|
|
SATOR |
AREPO |
TENET |
OPERA |
ROTAS |
sm |
|
ZS |
69 |
52 |
61 |
52 |
69 |
303 |
|
FS |
54 |
40 |
61 |
40 |
54 |
249 |
|
|
|
|
|
|
|
552 |
Die komplementäre Zahlenanordnung
verlangt jedoch
SATOR OPERA TENET AREPO ROTAS
Diese Lesart ist noch weniger
verständlich als die erste, weswegen es leichter fällt, nach einer anderen Lösung
als die wörtliche – die immer noch unflexibel betrieben wird – zu suchen. Die
Antwort habe ich bereits unter Bedeutung des SQ gegeben: TENET muß doppelt gelesen werden, OPERA hat zwei verschiedene Bedeutungen:
SATOR OPERA TENET, TENET
OPERA ROTAS
Der natürliche Ablauf des
komplementären Zahlenpalindroms liefert vertikal zweimal die Buchstabenform NN, horizontal, von unten links nach
rechts gewunden nach oben, zweimal SS. Die sinngemäße Lesart – die ich in zwei
Beiträgen
dargestellt habe – führt jedoch zu den Buchstaben NUI und SUI.
4.
Die inhärente Ordnung der komplementären Numerierung erschließt
sich wie so oft durch die Ermittlung der Faktorenwerte (FW) und ihre Kombination mit den ZS. Besondere Aufmerksamkeit verdient der äußere
Quadratrahmen und das Achsenkreuz, aber auch andere Strukturelemente.
III. Zahlenverhältnisse im komplementären Palindrom (kP)
a) ZS+FS der Zahlen
1-25
e) Das Gitter
a)
ZS+FS der Zahlen 1-25
Die ZS+FS der Zahlen 1-25 sind 325+220 = 545 = 5*109 = FW 114
= 6*19.
Die Werte zeigen einige Parallelen
zum SQ: Der Primfaktor 109 ist ZW des TENET-Kreuzes, im Produkt 6*19 ist die ZW 69 und 61
der Wörter SATOR TENET zu erkennen. In der Primzahl 109 zeigt sich, daß die Zahl 19 aus 10+9 zusammengesetzt ist, d.h. aus 2*5 Radialelementen + 9 Durchmesserelementen des
Tetraktyssterns, aber auch jedes 5*5 Punkte-Quadrats.
1.
Der äußere Quadratrahmen besteht aus 16 Punkten, was eine ZS von 16*13 = 208 ausmacht. Stellt man die Numerierung der linken (1-5) und rechten (21-25) Vertikalseite einander gegenüber,
bleiben für die obere (6, 15, 16) und untere (10, 11, 20) jeweils drei Zahlen übrig. Es ergibt sich somit zweimal das
Verhältnis von 5:3 Punkten.
|
|
1-5 |
21-25 |
sm |
ob. |
unt. |
sm |
GS |
|
FS |
15 |
65 |
80 |
21 |
27 |
48 |
128 |
|
|
5*(3:13) |
|
3*(7:9) |
|
|
||
Die Summe der Verhältniszahlen ist
jeweils 16, also ist das FS-Verhältnis 5:3 gleich dem Verhältnis der vertikalen zur horizontalen
Zahlenmenge. Das FS:ZS-Verhältnis
ist 128:208 = 16*(8:13). Der durchschnittliche FW je Zahl ist also 8.
Das doppelte Verhältnis 3:5 nimmt eine zentrale Stellung in
der trinitarischen Struktur des Dezimalsystems ein. Im Tetraktysstern wird der hexagonale Kreis mit 3 Radialelementen umfaßt durch
einen erweiterten Kreis mit 5
Radialelementen. Als selbständige Kreise aufgefaßt, haben sie das
Flächenverhältnis 1:3, als Flächenaufteilung das
Verhältnis 1:2. Der Verdoppelung der
Verhältniszahlen zu 6+10 = 16
entspricht die Summe der Zahlen 1-3 und 1-4, und man erhält somit die Zahl 7, die Summe der Flächeneinheiten
aus den beiden Zählungen. In der Zusammensetzung beider Aspekte erhält man die
dreistellige Zahl 167, die sich auch ergibt aus der Addition der Zahl 123 und ihres FW 44.
Die Zahl 128, aufgeteilt in 4*32, kann besagen, daß jede
Quadratseite aus 3+2 Punkten besteht.
2.
Die FS der Zahlen von 1-25 ist 220. Daher ist das FS-Verhältnis
von äußerem Quadratrahmen (16 Zahlen) zum inneren Quadrat (9 Zahlen) 128:92 = 4*(32:23). Im SQ sind beide Verhältniszahlen
vertreten. Die numerierten 10 Punkte der Tetraktys können in die Summen 32:23 aufgeteilt werden. Der Zahl 4 entspricht die Zahl der
Quadratseiten.
3.
Die Zahlen 3 und 2
sind die Grundzahlen der Radial- und Durchmesserelemente des Kreises. Durch ein
zweites Radialmaß des Tetraktyssterns und des 5*5 Quadrats werden 3 Radialelementen zu 5 erweitert. Auf die Produktzahen 5*7 der
zweistelligen Zahl 35 könnte
die Catullschen Numerierung der beiden Gedichte zurückgehen.
1.
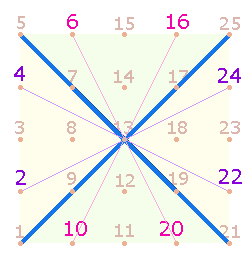
Zu unterscheiden ist das horizontal-vertikale und das
diagonale Achsenkreuz sowie innere und äußere Achsenkreuze:
|
5 |
6 |
15 |
16 |
25 |
|
4 |
7 |
14 |
17 |
24 |
|
3 |
8 |
13 |
18 |
23 |
|
2 |
9 |
12 |
19 |
22 |
|
1 |
10 |
11 |
20 |
21 |
Unter Weglassung der
Mittelpunktszahl 13
ergeben sich folgende FS:
|
|
hor. |
vert. |
sm |
li.u. |
re.u. |
sm |
|
inn. |
14 |
16 |
30 |
23 |
26 |
49 |
|
auß. |
26 |
19 |
45 |
11 |
15 |
26 |
|
|
40 |
35 |
75 |
34 |
41 |
75 |
|
40:35 = 5*(8:7) |
|
|
|
|||
|
30:35 = 15*(2:3) |
|
|
|
|||
Die FS beider Achsenkreuze ist jeweils 75 = 3*5*5, ihr jeweiliger FW 13 stimmt mit der Mittelpunkts- und
Primzahl 13 überein. Die Werte des
horizontal-vertikalen Achsenkreuzes geben durch zwei Verhältnisse eine Deutung.
Aus 8+7 Elementen besteht der DR-Rahmen,
aus 2+3 Elementen entweder die 5 DM-Elemente des hexagonalen Kreises oder aus 2+3 Radialelemente des Tetraktyssterns, wobei die 3 hexagonalen durch die äußeren
Achsenwerte und die 2
Erweiterungselemente durch die hexagonalen wiedergegeben werden. Die Aufteilung
der Radialelemente in 3+2
steht für das Flächenverhältnis 1:2 des
hexagonalen Kreises und des äußeren Kreisrings. Man wird also die Faktoren 3*5*5 aufteilen in 3*5*(3+2) und ihnen die Flächeneinheiten (1+3)+(1+2) = 7 zuteilen:
|
|
2.
Auch die Einzelziffern 7 und 5 als Punkte der DR sind auf Flächengrößen beziehbar,
indem die volle Zahl (5+2)
der Punkte 3
Flächeneinheiten, die Hexagonalpunkte (5) 1 Flächeneinheit repräsentieren:
|
|
Insofern die Zahl 35 aus 5*7 besteht, geben die Einzelziffern
als Radialelemente und DR-Punkte jeweils das Flächenverhältnis 1:3 wieder.
3.
Innerhalb des diagonalen Achsenkreuzes bleiben auf jeder
Quadratseite 2
Zahlen übrig:
|
|
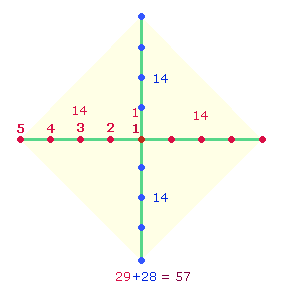
Von oben links beginnend haben die
4 komplementären Zahlenpaare
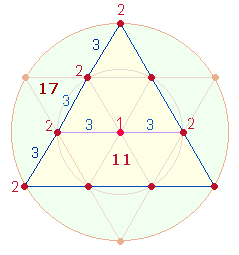
folgende FS: (14+15)+(11+17). Die ersten beiden Werte lassen sich dem Rahmen eines DR-Kreuzes, 11 und 17
der numerierten
Kreisachse und einer Tetraktysseite zuordnen. Die zwei addierten Werte 29+28 entsprechen einem numerierten
Achsenkreuz AK5,
woraus sich durch Winkelverschiebung ein 5*5-Punkte Quadrat bilden läßt.
|
|
4.
Die 25 Zahlen sind nun aufgeteilt in vier Gruppen: den
Mittelpunkt und dreimal je 8
komplementäre Zahlen; ihre FW/FS sind (13+75+75)+57. Fügt man zur FS 40
der Mittelachse den FW 13 des Mittelpunktes hinzu, erhält
man die Umkehrwerte 53+35
= 88 und damit ihre
Bedeutung als zweimal 3+5
Radialelemente des erweiterten Achsenkreuzes bzw. des Tetraktyssterns.
Es bietet sich nun das FS-Verhältnis der 9 Zahlen des horizontal-vertikalen
Achsenkreuzes zu den übrigen 16
Zahlen an: 88:132 = 44*(2:3).
1.
Die horizontal-vertikale Achse bildet mit jeweils zwei
benachbarten äußeren Zahlen ein erweitertes Achsenkreuz. Die rechte Grafik
zeigt die FW:
|
|
|
Ohne die Werte der 8 diagonalen Eckpunkte und des
Mittelpunkts beträgt die FS von
16 Zahlen 132, mit der 13 des Mittelpunkts 145 = 5*29.
Die 17 FW lassen sich aufteilen in 5 Zahlen des Innenkreuzes und 12 Randzahlen. Den 4*3 Randzahlen entspricht die Summe 4 3 des Innenkreuzes.
2.
Die 4 Buchstabengruppen haben folgende FS:
|
li. |
re. |
sm |
u. |
o. |
sm |
GS |
|
9 |
45 |
54 |
27 |
21 |
48 |
102 |
|
9*(1:5) |
3*(9:7) |
|
||||
|
54:48 = 6*(9:8) |
|
|||||
Das Verhältnis 54:48 kann auf zweifache Weise verstanden
werden. Es läßt sich erstens
auf zwei numerierte Tetraktysrahmen beziehen:
|
|
Die Zahlen 9 und 8 beziehen sich auf 3 Linien und 4 Punkte einer Tetraktysseite mit den
Numerierungen 3 und 2. Die Zahl 102 ist die FS der Zahlen 1-16 und auch von Bedeutung für das
SATOR-Quadrat: Sie ist die Zahlensumme seiner 8 verschiedenen Buchstaben, und das Wort ROTA – Rad hat den ZW 51 = 3*17.
Zweitens, durch 3 geteilt, bezeichnen die Zahlen 18 und 16 die Summen von Punkten und
Linien, die sich aus einer vierfachen Zählung von unnumerierten und numerierten
Durchmesser- und Radialelementen ergeben:
|
|
3.
Wenn man der horizontalen Achse den Mittelpunktswert 13 zuordnet, erhält man folgende
Verhältnisse der Innenzahlen zu den Außenzahlen:
|
horizontal |
vertikal |
|
||||
|
in. |
au. |
sm |
in. |
au. |
sm |
GS |
|
27 |
54 |
81 |
16 |
48 |
64 |
145 |
|
27*(1:2) |
16*(1:3) |
|
||||
Die Verhältiszahlen spiegeln die –
bereits genannten – Flächenverhältnisse der Tetraktyskreise wider und
bestätigen in zweistelliger Zusammensetzung die 25 Punkte des 5*5-Quadrats. Die Gesamtsumme 145 erweist sich als Addition der
Quadratzahlen 9²+8².
4.
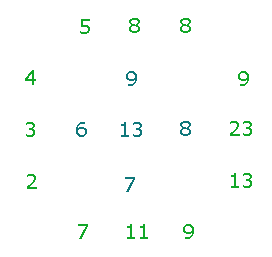
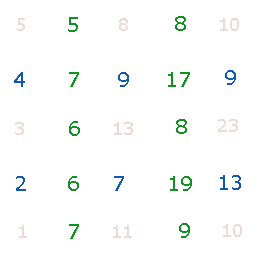
Eine Besonderheit bietet die Vertikalachse: Die 6 Rahmenzahlen haben ebenso die FS 48 wie die 5 Zahlen der Vertikalachse:
|
|
Die Zahlen 7 und 9 kommen doppelt vor, die Zahl 13 setzt sich aus 5+8 zusammen. Die Zahlen 11 und 8 sind die gemeisamen Bindeglieder.
Die Zahlen 11 und 8 entsprechen den addierten 5 Durchmesser- + 6 Radialelementen der Hexagonachse sowie der doppelten
Zählung 4+4 der Tetraktyserweiterung:
|
|
Hier zeigt sich die Bedeutung der
Zahl 26 als 2*13 Radialelemente, aufgeteilt in (3+2)+(3+5) = 13 und den Flächenentsprechungen der beiden
konzentrischen Kreis (1+2)+(1+3) = 7. Dafür spricht auch die FS 77 der 9 FW. Die Zahl 77 ist die FS der Zahlen 1-13. Das Verhältnis zur restlichen FS ist 77:143 = 11*(7:13).
Hierbei bezeichnet die Zahl 7
die Summe der Flächeneinheiten und 13 die Summe der entsprechenden Radialelemente.
Die gemeinsame Werte der
Außenglieder und der inneren Vertikalachse betragen 29. Ihre Summe 58 gibt wiederum in den Einzelziffern die relevanten Radialelemente
wieder. Die Gesamt-FS 145 teilt sich somit auf in das
Verhältnis 29*(2:3).
Die FS 29 der inneren Vertikalachse bewirkt, daß das oben
ermittelte Verhältnis 16*(5:3)
der linken und rechten Rahmenseite (10 P, FS 80) zu den inneren 2*3 Rahmenzahlen auch für die 5 Punkte der Mittelachse gilt: also
5*(2:1) Punkten entsprechen die FS 80:48 = 16*(5:3).
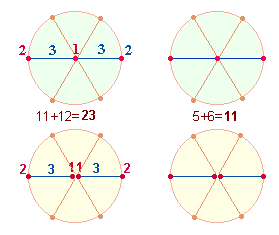
1.
Die ungeraden Zeilen bilden ein Gittermuster von 16 Punkten. Die übrigen 9 Punkte bilden ein 3*3 Quadrat. Die rechte Grafik zeigt
die FW:
|
|
|
Die 2*3 horizontalen Punkte haben jeweils die FS 22, die 2*5 vertikalen Punkte die FS 31+61 = 92, wobei die Zahl 31 die Mittelpunktszahl von 61 ist. Das Verhältnis der 10:6 Punkte ist demnach 92:44 = 4*(23:11).
Die Verhältniszahlen 23 und 11 sind von den unnumerierten und
numerierten DM- und Radialelementen der drei Hexagonachsen bekannt:
|
|
Sie sind als übertragen auf die
jeweils 5 Punkte der 4 Quadratachsen zu verstehen.
2.
Die Zahl 136 ist die Summe der Zahlen 1-16. Aus 16 Punkten besteht der Quadratrahmen, aus 16 Linien ein Achsenkreuz. Die Zahl 16 ist die Summe aus den Zahlen 1-3 und 1-4.
Durch passende Zuordnung ergibt
sich für jeweils 5:3 Punkte ein ZS+FS-Verhältnis von 3:5 und
der gemeinsame Teiler 43:
|
|
ZS |
FS |
|
|
ZS |
FS |
|
|
vert.li. |
40 |
31 |
71 |
vert.re. |
90 |
61 |
151 |
|
hor.unt. |
36 |
22 |
58 |
hor.ob. |
42 |
22 |
64 |
|
|
|
|
129 |
|
|
|
215 |
|
129:215 = 43*(3:5) |
|||||||
1.
Hinsichtlich der Werte der Horizontalzeilen darf man nicht
von vorneherein Parallelen zum SATOR-Quadrat oder zu Catulls gematrischer
Konstruktion im Auge haben, sondern sie in ihrem eigenen
Sinnzusammenhang untersuchen. Die ZS+FS der horizontalen und vertikalen Zeilen sind:
|
|
|
|
|
|
ZS |
FS |
GS |
fl.Ad. |
|
5 |
6 |
15 |
16 |
25 |
67 |
36 |
103 |
103 |
|
4 |
7 |
14 |
17 |
24 |
66 |
46 |
112 |
215 |
|
3 |
8 |
13 |
18 |
23 |
65 |
53 |
118 |
333 |
|
2 |
9 |
12 |
19 |
22 |
64 |
47 |
111 |
444 |
|
1 |
10 |
11 |
20 |
21 |
63 |
38 |
101 |
545 |
|
|
|
|
|
|
325 |
220 |
545 |
|
Die konzentrische Betrachtung der FS zeigt Zusammengehörigkeit von 36+38 = 74 und 46+47 = 93,
zusammen 167. (Über die Zahl 167 s.o.) Die ZS+FS der geraden Zeilen sind 66+64 = 130 = 10*13; 46+47
= 93 = 3*31. Die Gesamtsummen sind 112+111 = 223. Die Summen der ungeraden Zeilen
ergeben den Umkehrwert 322.
Wie die Summe 333 der obersten 3 Zeilen und die
Summe 444
der Zeilen 1-4 zeigen, sind die Einzelziffern der beiden Umkehrzahlen 2+2+3 auf die 3 Linien und 4 Punkte einer von 3 Tetraktysseiten zu beziehen, oder
alternativ, auf 3
hexagonale Segmentelemente und 2+2 Erweiterungselemente. Eine ZW/FW-Verrechnung der beiden Umkehrzahlen ergibt:
|
|
|
|
sm |
FW |
sm |
FW |
|
ZS+FS |
223 |
322 |
545 |
114 |
|
|
|
FW |
223 |
32 |
255 |
25 |
|
|
|
sm |
|
|
800 |
139 |
939 |
316 |
|
FW |
|
|
20 |
139 |
159 |
56 |
|
sm |
372= 12*31 |
|
372 |
|||
Das Produkt 15*17 weist auf die Numerierungssumme 17
einer Tetraktysseite hin. Die Gesamtsumme dieser Numerierung beträgt jedoch 45,
auf eine Tetraktysseite bezogen also 15. Die Summe 939 = 3*313 läßt sich auf 3
DR beziehen, jede gekennzeichnet durch das Punktemuster 3+1+3. Die 15 Elemente
des DR-Rahmens werden durch umlaufende Numerierung um 2 auf 17 Positionen
erweitert bzw. von 7
Punkten auf 9
Positionen. Wenn die 10.
Position einmal mit einer (nicht zählbaren und unsichtbaren) Ziffer 0 und einmal mit der zweiziffrig zu
denkenden 10
besetzt wird, beträgt, wie in der Tabelle der Zuwachs von 8 bis 10, wie in der Tabelle zu ersehen, 111 und 112:
|
|
Das Produkt 12*13 des Endergebnisses zeigt nicht nur
die 7 Flächeneinheiten der 2 Tetraktyskreise, sonden auch 31+12 Elemente eine DR-Kreuzes, das zu einem Oktaeder
zusammengefügt werden kann.
2.
Betrachtet man die 5 Zeilen als Durchmesserelemente und
will auch 6 Radialelemente berücksichtigen, sind die Werte der Mittelachse zu
verdoppeln und die ZS+FS
neu zu bestimmen. Dies läßt sich auch für die Vertikalachse durchführen:
|
|
|
|
sm |
|
|
sm |
GS |
|
ZS |
325 |
65 |
390 |
325 |
65 |
390 |
|
|
FS |
220 |
53 |
273 |
220 |
48 |
268 |
|
|
|
545 |
118 |
663 |
545 |
113 |
658 |
1321 |
Die Zahlen 13 und 21 bezeichnen die Summen der
Hexagonal- und Gesamtelemente der Doppelraute und repräsentieren somit das
Flächenverhältnis 1:2.
Die ZS+FS der beiden Mittelachsen beträgt 118+113 = 231, die Summe der Zahlen 1-21.
Das FS:ZS-Verhältnis der 6 horizontalen Radialzeilen beträgt 39*(7:10). Die ZS+FS der 1. und 3. Zeile von oben
103+118 = 221 = 13*17 beträgt ein Drittel der Gesamtsumme 663.
3.
Die ZW/FW-Verrechnung der addierten 5+6 Werte ergibt:
|
|
ZS+FS |
sm |
FW |
sm |
FW |
|
|
hor. |
545 |
663 |
1208 |
157 |
|
|
|
ver. |
545 |
658 |
1203 |
404 |
|
|
|
sm |
|
|
2411 |
561 |
2972 |
747 |
|
FW |
|
|
2411 |
31 |
2442 |
53 |
|
sm |
|
|
|
|
|
800 |
Die FS 561 = 33*17 ist die Summe der Zahlen 1-33 und liegt den Zahlenwerten des SATOR-Quadrats zugrunde, da die
Einzelziffern die Summe 51
ergeben: 51*11 = 561. Die Umkehrformation 2442 bezieht sich auf 2 Tetraktys mit 2*3*4 = 24 Punkten als Teilzahl, die sich
durch 2*3*3 = 18 Linien zur Ganzzahl 42 vervollständigt.
IV. Die 25 Werte
von c 5 und 7 im 5*5 Quadrat
1.
Die ZS+FS der 25
Verse sind:
c5
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
293 |
349 |
325 |
324 |
326 |
300 |
217 |
300 |
333 |
266 |
281 |
358 |
308 |
|
|
174 |
228 |
193 |
245 |
220 |
225 |
169 |
249 |
263 |
190 |
194 |
237 |
209 |
|
|
467 |
577 |
518 |
569 |
546 |
525 |
386 |
549 |
596 |
456 |
475 |
595 |
517 |
6776 |
|
6776 =
22*308 |
|||||||||||||
c7
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
302 |
331 |
361 |
267 |
315 |
359 |
336 |
348 |
203 |
351 |
280 |
286 |
|
3739 |
|
202 |
224 |
240 |
205 |
220 |
262 |
240 |
242 |
156 |
248 |
206 |
218 |
|
2663 |
|
504 |
555 |
601 |
472 |
535 |
621 |
576 |
590 |
359 |
599 |
486 |
504 |
|
6402 |
|
6402 =
22*291 |
|||||||||||||
2.
Eine Anordnung vorstehender Werte nach dem Muster des SQ findet sich unter C5C7-SQ. Es wird dabei deutlich, daß der 13. Vers von c. 5 den Mittelpunkt
des SQ bildet, und da sowohl die ZS als auch die FS durch 11 teilbar ist – 11*(19:28) – diese Mittelpunktwerte auch für
c. 7 gelten können.
3.
Die ZS und FS der beiden Gedichte lassen sich auch linear
untersuchen. Dabei sind in vertikaler Gruppierung vier Teilungen durch 11
erkennbar.
293 349 325 324 326 300 217 300 333 266 281 358
308
174 228 193 245 220 225 169 249 263 190 194 237
209
302 331 361 267 315 359 336 348 203 351 280 286
202 224 240 205 220 262 240 242 156 248 206 218
Die vier Ergebnisse sind:
6490
= 590*11; 2101 = 191*11; 4587 = 3*139*11; 517 = 47*11. Die 13 Positionen teilen sich
auf in der Reihenfolge 6+2+4+1. In vierstelliger Zusammensetzung ist 6241 die Quadratzahl von 79. 2*79 = 158 ist die ZS von NET OPERA
SATOR – Es webt der
Schöpfer die Werke und ließe sich zusammensetzen aus SATOR+EE und OPRATN.
Die Einzelziffern von 6241 geben die Elemente des
sanduhrförmigen Doppeldreiecks im Hexagon wieder:
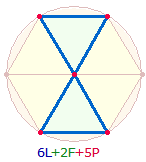
Die 5 Punkte sind aufgeteilt
in 4
Kreislinienpunkte + Mittelpunkt. Von besonderem Interesse ist, daß das Wort HOMO – Mensch die ZS+FS 79 hat: 48+31 = 79. 79
ist die Komplementärzahl zu 31.
Die Quadratzahl könnte auf die Zweigeschlechtlichkeit von Mann und Frau
hinweisen.
Das Hexagon enthält den
Doppelaspekt von 3*3 = 9 Punkten, die bei
einmaliger Zählung des Mittelpunktes um zwei auf 7 Punkte reduziert werden.
Erstellt: Oktober 2009