DIE KAPITOLINISCHE TRIAS

A. EINLEITUNG

I. Die KT als Vorbild für Vergils 10 Eklogen

II. VESTA

III. Modelle

B. HAUPTTEIL

I. Die KT als Vorbild für Vergils 10 Eklogen

1. Die Existenz römischer Gematrie ist bisher nicht durch literarische Belege und archäologische Funde nachgewiesen, aber nachweisbar durch faktische Ergebnisse. Die gematrischen Werte der 6 Namen der Kapitolinischen Trias (KT) stellen einen so idealen Maßstab dessen dar, was die religiöse Bedeutung des dezimalen Zahlensystems ausmacht, daß VERGIL sie für die Verszahlen und Gliederung seiner 10 Eklogen verwendete. Worin die Gemeinsamkeiten bestehen, soll hier knapp zusammengefaßt werden.

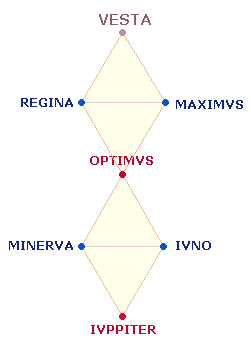
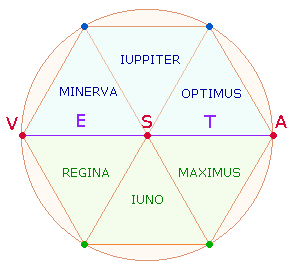
2. Die Eigenart der KT besteht darin, daß den drei Gottheiten IUPPITER IUNO MINERVA ebenso drei Beinamen entsprechen, aber so, daß zwei zu IUPPITER und einer zu IUNO gehören, während MINERVA leer ausgeht:

1.+2			2.+1		3.+0
IVPPITER			IVNO		MINERVA
	OPTIMVS	MAXIMVS		REGINA
3			2		1

Kennzeichen gematrischer Konstruktionen sind Zahlenverhältnisse, die ihren vollen Sinn stets in Kombination von Zahlensummen (ZS) und Faktorensummen (FS) gewinnen. Dies zeigt sich exemplarisch an den sechs Bezeichnungen der KT: Die drei Götternamen und die drei Beinamen in der Kombination der ZS+FS sind gleich:

	ZS	FS	sm
I I M	242	173	415
OMR	252	163	415
	494	336	830
494 = 2*13*19
336 = 3*7*16

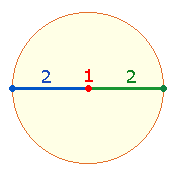
Vorbild dieser Gleichheit der Werte dürfte die mathematische Gleichung 1+2 = 3 sein. Auch der Kreis und das Hexagon mit zweimal drei Dreiecken sind von Bedeutung.

3. Die 10 Eklogen des Vergil sind auf folgende Weise gegliedert:

1	2	3	4	5	6	7	8	9	10
83	73	111	63	90	86	70	110	67	77
	247					247

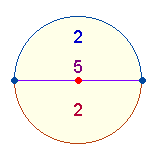
Die Zahl 10 setzt sich zusammen aus zweimal 5 Einheiten. 1 und 5, 6 und 10 bilden jeweils Anfang und Ende jeder Einheit. Die zwei umschlossenen Dreiergruppen haben jeweils die ZS 247 = 13*19, also jeweils die Hälfte der ZS 494 der 6 Kapitolinischen Namen. In paralleler Zuordnung beider Gruppen ist jedes der drei Zahlenpaare durch 13 teilbar: 73+70 = 143 = 11*13; 111+110 = 221 = 17*13; 63+67 = 130 = 10*13.

Die Summen der Umrahmungszahlen 83+90 und 86+77 sind identisch mit den beiden kapitolinischen FS 173 und 163.

4. Auch die Summe der 10 FW fügt sich zur kapitolinischen FS 336:

	1	2	3	4	5	6	7	8	9	10
ZS	83	73	111	63	90	86	70	110	67	77	830
FW	83	73	40	13	13	45	14	18	67	18	384

Das Verhältnis der beiden FS ist 336:384 = 48*(7:8).

II. VESTA

1. VESTA ist einerseits eine weibliche Gottheit, andererseits das übergreifende Sinnprinzip römischer Gematrie. Der Name ist zu verstehen als Gleichung V EST A: die untere Tetraktys ist gleich der oberen, repräsentiert durch den 20. und 1. Buchstaben. Nach dem bereits bekannten Gliederungsmuster sind die 5 Buchstaben den 5 Elementen der Kreisachse zuzuordnen:

SQ	V	E	S	T	A
ZW		5	18	19		42
	20				1	21
21:42 = 21*(1:2)

Bereits die Einzelziffern des Verhältnisses zeigen zweimal drei Radialelemente der Kreisachse:

2. Von beiden Bestandteilen des Namens VESTA lassen sich nicht nur die ZS und FS, sondern auch deren FW ermitteln:

	ZS	FS	sm	FW1	FW2	sm	GS
VA	21	10	31	10	7	17	48
EST	42	32	74	12	10	22	96
	63	42	105	22	17	39	144

Das Verhältnis der Endsummen der 4Werte 48:96 beträgt wie das der ZS 21:42 wiederum 1:2. Die beiden Endsummen erweisen sich als Kernbausteine der FS der 6 kapitolinischen Namen:

IVPPITER	78			IVNO	37
OPTIMVS	66			REGINA	49
		MAXIMVS		MINERVA	58
	144		48		144
144:48:144 = 48*(3:1:3)

3. Das FS:ZS-Verhältnis des Namens VESTA ist 21*(2:3). Die Verhältniszahlen 3 und 2 lassen sich als drei Radialelemente der Kreisachse und zwei Elemente zur Ergänzung der 5 Durchmesserelemente verstehen. Das Differenzverhältnis zwischen FS und ZS beträgt 2:1.

Dieselben Verhältnisse verkörpert die Zahl 9 allein: 6:9 = 3*(2:3). Die Buchstabenentsprechung der Zahl 9 ist das I. In den 6 kapitolinischen Namen ist es 7 mal enthalten, vertritt also mit seiner ZS 63 den Namen VESTA.

Das Verhältnis 2:3 besteht schließlich zwischen der ZS+FS der Vokale und Konsonanten:

	ZS	FS	sm
Vok.	209	123	332
Kons.	285	213	498
	494	336	830
332:498 = 166*(2:3)

4. Durch seine ZS 63 bezieht sich VESTA auf die Figur der Doppelraute (DR), die aus 21 Elementen besteht und dreimal im Tetraktysstern zu erkennen ist. Eine DR besteht wie das Hexagon aus 7 Punkten. Da inzwischen die Bedeutung VESTA für die KT deutlich geworden ist, liegt es nahe, sie den 6 Namen hinzuzufügen:

Ein Achsenkreuz aus zwei DR kann zu einem Oktaeder zusammengefügt werden. Die zweite DR kann mit den FS der 6 Namen besetzt werden. VESTA bleibt unsichtbar im Hintergrund, da bei der Oktaederbildung ihr Platz mit dem von IUPPITER zusammenfällt. Der Oktaeder hat 6 Ecken. Ihre vereinten Werte weisen auf jeweils 2*2 bzw. 2*6 Tetraktys hin:

	ZS	FS	sm	FW1	FW2	sm	GS
IVPPITER	109	78	187	109	18	127	314
VESTA	63	42	105	13	12	25	130
	172	120	292	122	30	152	444
292 = 4*73; 444 = 12*37

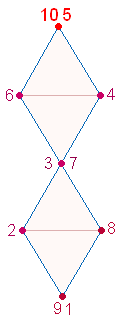
Ein Numerierungsmodus der DR zeigt auf dem Platz der VESTA die Zahlen 10 und 5, die in dreistelliger Zusammensetzung 105 der ZS+FS von VESTA entsprechen:

III. Modelle

1. Zu Beginn dieses Abschnittes muß ein entscheidende Frage geklärt werden. Ein geometrisches Modell kann sinnvollen Kriterien entsprechen, aber kann es auch als historische Rekonstruktion gewertet werden? Die Frage mag in anderen Zusammenhängen weniger wichtig zu sein, im Falle der Kapitolinischen Trias ist sie mit einem unbedingten Ja zu beantworten, sonst kann man hier abbrechen und sich mit dem bisher Gesicherten begnügen. Denn das zentrale Modell des Doppelrautenkreuzes führt zu neuen Ergebnissen, deren Existenz ich bei VERGIL und OVID nachzuweisen versuchte. Im Rahmen dieser Einleitung geht es um eine überzeugende Begründung von zwei Modellen.

2. Das erste Modell orientiert sich wiederum an der Kreisachse, die aus 5 Elementen besteht. Diese teilt sowohl die Kreislinie als auch die Kreisfläche in zwei Teile. Beide sind als jeweils 2 Elemente anzusehen. Die Kreisteilung führt zu einer Gesamtzahl von 9 Elementen:

Eine Hälfte ist nur zu definieren aus 2+5 Elementen, für die zweite Hälfte bleiben dann 2 Elemente übrig. Um die Ungleichheiten auszugleichen, ist der Kreis zweimal zu berechnen, einmal als je eigenständig definierte Hälfte und einmal im Ganzen: (7+7)+9 = 23.

Überträgt man dieses Prinzip auf das Hexagon, besteht jede Hälfte ohne Achsenelementen aus 10 Elementen. Das Zahlenverhältnis der ersten Hälfte zur zweiten ist demnach (10+5):10 = 5*(3:2). Die analoge Gesamtrechnung lautet (15+15)+25 = 55. Da die Summe der Zahlen 1-10 55 beträgt, ist dieses Hexagon-Ergebnis von besonderer Bedeutung.

3. Nimmt man VESTA als siebten Namen in die KT auf, ist die Gesamtzahl der Buchstaben 44 und aufteilbar in 2*22. Letzteres ist möglich, da die drei Namen JUPPITER OPTIMUS MAXIMUS bereits eine Hälfte von 22 Buchstaben ausmacht. Wie OPTIMUS MAXIMUS besteht auch MINERVA aus 7 Buchstaben. Wenn man nun MAXIMUS gegen MINERVA austauscht, erhält man ein Zahlenverhältnis der ZS+FS:

	ZS	FS	sm		ZS	FS	sm
IVPPITER	109	78	187	MAXIMUS	93	48	141
OPTIMUS	107	66	173	IUNO	56	37	93
MINERVA	77	58	135	REGINA	52	49	101
				VESTA	63	42	105
	293	202	495		264	176	440
495:440 = 55*(9:8)

Den Austausch der beiden Namen ist im geometrischen Modell zu erreichen, wenn man die kapitolinischen Namen den 6 Dreiecken zuordnet und mit IUPPITER in der oberen Mitte beginnt:

Die Mittelachse VESTA wird benötigt, um die untere Hexagonhälfte zu definieren. Wenn man für jedes Dreieck 7 Elemente zählt, ergibt sich für die untere und obere Hälfte die Rechnung 26+21 = 47. Nun ist die ZS von DEUS – Gott 47 und die FS 26. Die Summe 21 ist die Differenz zwischen FS und ZS. Die ZS 47 + FS 26 von DEUS ergibt demnach die Summe 73, die für die ZS+FS von IUPPITER VESTA das Vierfache betrug.

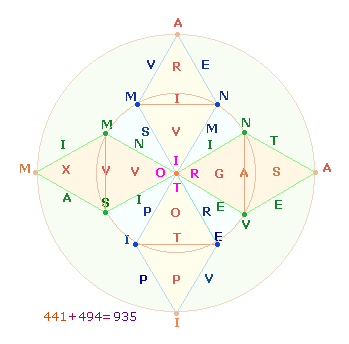
4. Zweimal 22 Buchstaben kann man auf einem DR-Kreuz anordnen, indem man die für das Hexagon gefundene Reihenfolge einhält. Der Mittelpunkt wird dabei für jede einzelne Raute besetzt. Die Anordnung erfolgt in Zickzack-Form:

Aus den 4 Buchstaben des Mittelpunktes und 4 Buchstaben der äußeren Punkte lassen sich die Anagramme ORTI MAIA ermitteln. Diese beiden Wörter haben, wie ich glaube nachgewiesen zu haben, VERGIL und OVID in der Aeneis und den Metamorphosen durch gematrische Konstruktionen berücksichtigt.

5. Neben diesem Sondermodell dürften noch drei weitere DR-Kreuz-Modelle existiert haben. Das erste entspricht dem Sondermodell, hält aber die reguläre Reihenfolge IUPPITER OPTIMUS MAXIMUS ein. Das zweite beginnt in jeder DR mit ES – Du bist, das dritte fügt zu ES noch VESTA hinzu. Die Buchstabenzahlen sind dann 43+44+48 = 135. In ersterem Fall besteht der Mittelpunkt aus 2+1 Buchstaben, in letzterem sind jeweils 24 Buchstaben je DR nach einem bestimmten Numerierungsmuster unterzubringen:

Diese insgesamt vier Muster sind auf einer eigenen Seite dokumentiert.

Erstellt: Januar 2013

Inhalt