Bedeutung der Faktorenwerte

I. Einleitung

II. Differenzverhältnis zwischen Faktorenwert und Zahlenwert

III. Die 4Werte

IV. Tabellen

I. Einleitung

1. Im Unterschied zu den Griechen gingen die Römer weniger abstrakt mit den Zahlen um, sondern versuchten, sie in ihrer Bedeutung zu verstehen. Göttliche Ordnung war für sie Vorbild für menschliche Ordnung. Göttliches manifestierte sich in den Zahlen. Sie griffen auf, was sie an Zahlenspekulationen vorfanden, wie etwa das pythagoreische System, und entwickelten es selbständig weiter. Was die Römer an objektiven Erkenntnissen gewannen, ist rekonstruierbar. Dieser Aufgabe habe ich mich unterzogen. Grundsätzliches habe ich unter "Entwicklung des Dezimalsystems" dargelegt. Dort werden geometrische Modelle vorgestellt.

Zu den Prinzipien der Zahlenbetrachtung gehört, daß sich alle Zahlen einem Ursprung verdanken, aus dem sie hervorgehen.

2. Wenn man einmal anfängt, alles nach seiner Bedeutung erkennen zu wollen, dann erscheint es nicht zufällig, daß es Zahlen gibt, die nur aus einem Faktor bestehen und Primzahlen genannt werden und solche, die aus Primfaktoren zusammengesetzt sind.

Wie man nun Zahlen nach verschiedenen Gesichtspunkten zusammenzählen kann, so ist das auch bei der Zählung von Primfaktoren der Fall. Die Zahl 12 z.B. besteht aus den Primfaktoren 2*2*3, die Addition der drei Primfaktoren ist sodann ihr Faktorenwert 7.

Wenn man daran geht, Primfaktoren von Zahlen zu addieren, ist die derzeit nach pragmatischen Gesichtspunkten gefaßte Definition von Primzahlen hinfällig, gemäß der die Zahl 1 nicht zu den Primzahlen zu rechnen ist. Sie bei der Zählung von Primfaktoren zu ignorieren, wäre gegen jede Logik. Vielmehr ist die Definition von Primzahlen sachgerecht so zu formulieren:

3. Wenn man nun zwei Additionsreihen von Zahlen und ihren Faktoren erstellt, entdeckt man, daß es proportionale Beziehungen zwischen beiden geben kann. Damit die gemeinsamen Teiler sichtbar bleiben, habe ich folgende Konvention eingeführt: Die Faktorensumme (FS) der Zahlen 1-21 ist 165 = 5*33, die Zahlensumme (ZS) 231 = 7*33. Ich stelle das Verhältnis dann so dar: 33*(5:7). Ich stelle die Verhältniszahl der FS voran, damit die Differenz zur Verhältniszahl der ZS besser sichtbar wird. Für Primzahlen gilt, daß Zahlenwert (ZW) und Faktorenwert (FW) identisch sind. Dies führt zu folgender Unterscheidung von Primzahlen und zusammengesetzten Zahlen:

Die Summe der Primzahlen von 1-21 ist 78, die Summe der zusammengesetzten Zahlen 231-78 = 153. Die Differenz der identischen FS 78 der Primzahlen zur gesamten FS 156 beträgt 87. Es ergibt sich folgende Rechnung für die ZS+FS:

	ZS	FS	sm
PZ	78	78	156
zsg.Z.	153	87	240
	231	165	396

Die ZS+FS der Primzahlen und der zusammengesetzten Zahlen haben das Verhältnis 156:240 = 12*(13:20). Einige weitere Verhältnisse folgen weiter unten. Nach vorigem Muster füge ich noch ZS und FS der Zahlen 1-13 hinzu. Alle Einzelwerte sind durch 7 teilbar:

	ZS	FS	sm
PZ	42	42	84
zsg.Z.	49	35	84
	91	77	168

Besonders erwähnen möchte ich die Zahlen 11-100, deren 21 Primzahlen und 69 zusammengesetzten Zahlen das FS-Verhältnis 149*(7:8) bilden. Sie sind ein beeindruckendes Beispiel für die ontologische Einheit von Zahl und Geometrie.

4. ZW+FW, ZS+FS bilden eine Sinneinheit, die einmal leichter, einmal schwerer deutbar ist. Die Zahl 17 z.B. besitzt u.a. Bedeutung durch die Addition der Zahl 10 und ihres FW 7. Die Zahl 11 erweist dadurch einen besonderen Stellenwert, daß 123 als dreistellige Zusammensetzung der Zahlen 1-3 sich aus der ZS 66 der Zahlen 1-11 und ihrer FS 57 zusammensetzt.

5. Ein Online-Programm berechnet Zahlenwerte und Faktorenwerte von Texten.

II. Differenzverhältnis zwischen Faktorenwert und Zahlenwert

1. Ist eine Zahl keine Primzahl, besteht eine Differenz zwischen FW und ZW. Es gibt zwei Betrachtungsmöglichkeiten: erstens, FW und ZW werden als eigenständige Größen behandelt und addiert, zweitens, FW + Differenz zum ZW bilden zusammen den ganzen ZW. Erstere Betrachtungsweise sei externes, letzteres internes Verhältnis (Differenzverhältnis) genannt. Z.B. das externe FW:ZW-Verhältnis von 12 ist 7:12, das Differenzverhältnis 7:5. Es ergeben sich daraus die Summen 19+12 = 31.

2. Da die Zahlen des Dezimalsystem einen Organismus bilden, indem nachfolgende Zahlen aus vorhergehenden zusammengesetzt sind, ist es von Bedeutung, eine Zahl (z) nicht nur für sich selbst, sondern auch als Endzahl einer Additionsreihe ab der Zahl 1 zu betrachten. Die bekannte Formel hierfür lautet: z/2*(z+1), für 10 ist also zu rechnen 5*11 = 55, für 11 5,5*12 = 66.

Addiert man auch FW fortlaufend, entsteht ein FS:ZS-Verhältnis. Als Verhältnis sei jedes Ergebis bezeichnet, im besonderen jedoch ein Ergebnis mit gemeinsamem Teiler.

Die nachfolgende Tabelle zeigt die ersten 9 Zahlenreihen (ZR) ab 1, die einen gemeinsamen Teiler (T) ab 3 haben. Um den gemeinsamen Teiler angemessen darstellen zu können, wird die nachfolgende Notationsroutine verwendet:

ZR	FS	ZS	T	FS:ZS	sm
8	33	36	3*	(11:12)	= 69
9	39	45	3*	(13:15)	= 84
11	57	66	3*	(19:22)	= 123
13	77	91	7*	(11:13)	= 168
16	102	136	34*	(3:4)	= 238
17	119	153	17*	(7:9)	= 272
20	155	210	5*	(31:42)	= 365
21	165	231	33*	(5:7)	= 396
24	210	300	30*	(7:10)	= 510
	957	1268			2225

Die Gesamtsumme 2225 = 25*89 verdient nähere Betrachtung und Deutung.

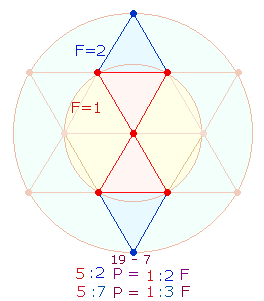
Die Zahlen 1-21, bedeutsam durch die 21 Buchstaben des lateinischen Alphabets (ohne Y, Z), sind ein anschauliches Beispiel für externes und internes FS:ZS-Verhältnis 5:7 und 5:2:

Der Tetraktysstern enthält drei Doppelrauten, bestehend aus jeweils 21 Elementen. Die 5 Punkte des hexagonalen Doppeldreiecks werden um 2 Punkte erweitert. Das Kreisflächenverhältnis des hexagonalen Kreises zum äußeren Kreisring beträgt 1:2 und zum ganzen äußeren Kreis 1:3. Diesen beiden Flächenverhältnissen entsprechen 5:2 und 5:7 Punkte der Doppelraute. Siehe auch Die Zahlen 1-21.

1. FS:ZS-Verhältnisse von Zahlenreihen (mit gemeinsamem Teiler) sind nur eine Weise, um ein näheres Verständnis von Zahlen, bis zu denen die Addition ab 1 führt, zu gewinnen. In den Ergebnissen können z.B. Grundstrukturen des Dezimalsystems erkannt werden, ZS und FS können außerdem addiert und miteinander verrechnet werden.

Nach der Zahl 25 sind FS:ZS-Verhältnisse mit gemeinsamem Teiler selten.

III. Die 4Werte

1. Von einer Gruppe von Zahlen lassen sich 4 Werte (4W) bilden: 1. die Zahlensumme (ZS), 2. die Faktorensumme (FS), 3. den FW der ZS (=FW1), 4. den FW der FS (=FW2).

Als Beispiel mögen die 5 Zahlen 14-18 dienen: ZS = 80, FS = 50, FW1 = 13, FW2 = 12. Die 4W können einander verschieden zugeordnet werden. Hier stehen ZS und FS mit den beiden FW in einem numerischenVerhältnis: ZS 80+FS 50 = 130; FW1+FW2 13+12 = 25; 130:25 = 5*(26:5) = 155 = 5*31. Der Durchschnitt der 4Werte für die 5 Zahlen ist demnach 31.

2. Bei einer gegebenen Anzahl von Buchstaben bleiben ZS und FS stets gleich, während FW1 und FW2 sich nach Wortlänge und Wortzahl richten: Sie sind also unterschiedlich im Wort AMORES – Liebesgeschichten und den zwei Wörtern AMOR ES – Du bist die Liebe:

	ZS	FS	sm	FW1	FW2	sm	GS
AMORES	67	47	114	67	47	114	228
AMOR	44	34	78	15	19	34	112
ES	23	13	36	23	13	36	72
	67	47	114	38	32	70	184

Das 4Werte-Verhältnis der beiden Wörter AMOR ES ist 112:72 = 8*(14:9).

Eine weitere Möglichkeit additiver Zusammenfassung besteht in der Zuordnung von FW1 zur ZS und FW2 zur FS, wie das Beispiel von PENSATOR zeigt: ZS 102+FW1 22 = 124; FS 80+FW2 13 = 93; 124:93 = 31*(3:4).

IV. Fortsetzung der Zahlenreihen

Die folgenden Tabellen stellen Zahlenreihen (ZR) ab 1 bis zur jeweiligen Endzahl mit deren Faktorenwert und der laufenden Faktorensumme und Zahlensumme dar:

ZR	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
FW	1	2	3	4	5	5	7	6	6	7	11	7	13	9	8
FS	1	3	6	10	15	20	27	33	39	46	57	64	77	86	94
ZS	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120

ZR	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
FW	8	17	8	19	9	10	13	23	9	10	15	9	11	29	10
FS	102	119	127	146	155	165	178	201	210	220	235	244	255	284	294
ZS	136	153	171	190	210	231	253	276	300	325	351	378	406	435	465

ZR	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50
FW	31	10	14	19	12	10	37	21	16	11	41	12	43	15	11	25	47	11	14	12
FS	325	335	349	368	380	390	427	448	464	475	516	528	571	586	597	622	669	680	694	706
ZS	496	528	561	595	630	666	703	741	780	820	861	903	946	990	1035	1081	1128	1176	1225	1275

51	20	726	1326	61	61	1021	1891	71	71	1312	2556
52	17	743	1378	62	33	1054	1953	72	12	1324	2628
53	53	796	1431	63	13	1067	2016	73	73	1397	2701
54	11	807	1485	64	12	1079	2080	74	39	1436	2775
55	16	823	1540	65	18	1097	2145	75	13	1449	2850
56	13	836	1596	66	16	1113	2211	76	23	1472	2926
57	22	858	1653	67	67	1180	2278	77	18	1490	3003
58	31	889	1711	68	21	1201	2346	78	18	1508	3081
59	59	948	1770	69	26	1227	2415	79	79	1587	3160
60	12	960	1830	70	14	1241	2485	80	13	1600	3240

81	12	1612	3321	91	20	1990	4186
82	43	1655	3403	92	27	2017	4278
83	83	1738	3486	93	34	2051	4371
84	14	1752	3570	94	49	2100	4465
85	22	1774	3655	95	24	2124	4560
86	45	1819	3741	96	13	2137	4656
87	32	1851	3828	97	97	2234	4753
88	17	1868	3916	98	16	2250	4851
89	89	1957	4005	99	17	2267	4950
90	13	1970	4095	100	14	2281	5050

ZS und FS mit gemeinsamem Teiler (2-stellig): 56 (76); 60 (30); 64 (13); 78 (13); 80 (40); 95 (12)

Erstellt: Dezember 2004

Letzte Änderung: 2024

domum

index