Die gematrischen Werte von
SENATUS POPULUSQUE ROMANUS
II.
POPULUSQUE
e) 10 Punktepositionen der DR
e) 10 Punktepositionen der DR
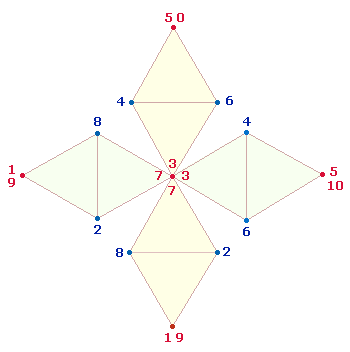
1. Die
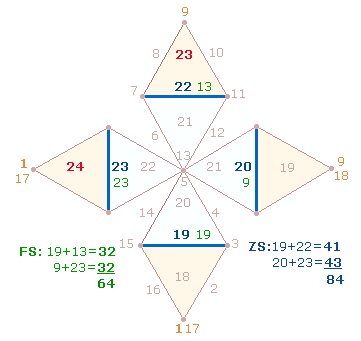
Doppelraute (DR) ist die eckige Schwester der Ziffer 8, die man kreisförmig umfahren kann.
Numeriert man auf diese Weise die Punkte der DR, bis man den Anfang erreicht,
erhält man 9 Positionen. Nun ist das Ziel des Tetraktyssterns die Erreichung
einer dreidimensionalen Figur, des Oktaeders. Durch die Vereinigung der
Endpunkte kommt eine weitere Numerierungsposition hinzu. Besetzt man die 10
Positionen einmal von 1-0 und einmal von 1-10, ergibt
sich ein gleiches FS:ZS-Verhältnis 17:20 der zweimal 6 vertikalen und 4
horizontalen Zahlen, 3*(17:20) und 2*(17:20):
|
|
Der
Buchstabe Q bezeichnet durch den Schrägstrich
das Überschreiten der 9. zur 10. Position. Sein ZW 16 geht
aus den nunmehr 6 (statt 7) Punkten + den 10 Linien hervor,
der ZW 20 des begleitende V aus den
nunmehr 20 Elementen der DR. Wenn nun die Verbindungspartikel
–QUE in der
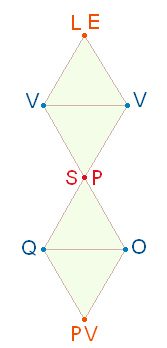
Kurzformel SPQR eine eigene Initiale bildet, könnte auch die
Besetzung der 10 Buchstaben von POPULUSQUE nach
dem besprochenen Numerierungsmodus eine bedeutende Rolle spielen:
|
|
Die ZS+FS der
horizontalen und vertikalen Buchstaben sind:
|
|
ZS |
FS |
sm |
|
QO-VV |
70 |
35 |
105 |
|
PV-SP-LE |
84 |
49 |
133 |
|
|
154 |
84 |
238 |
|
70:84 =
14*(5:6); 35:49 = 7*(5:7) |
|||
|
49:84 = 7*(7:12) |
|||
Alle
vier Werte sind durch 7 teilbar und bilden entsprechende Verhältnisse. Diese
sind im Folgenden näher zu betrachten.
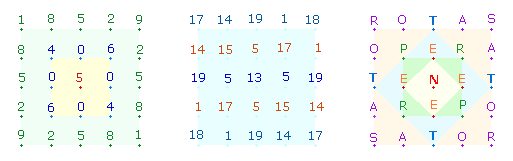
2. Die FS 35 der horizontalen
Buchstaben beträgt die Hälfte ihrer ZS 70. Die Kenner des gematrischen
Systems erkannten darin eine Parallele zum einstelligen 1x1-Modell des SATOR-Quadrats:
|
|
Nach
Abzug der fehlenden Zahlen 3 und 7 des linken
Quadrats bleibt von der Summe 45 der Zahlen 1-9 die
Summe 35 übrig. Die Zahlen einer jeden
Zeile bilden komplementäre Paare mit der Summe 10. Nach Häufigkeit (Hf) ergibt
sich:
|
|
1+9 |
2+8 |
4+6 |
5 |
35 |
|
Hf |
2 |
4 |
2 |
5 |
13 |
|
sm |
20 |
40 |
20 |
25 |
105 |
In
beiden Quadraten besteht die mittlere Zeile aus Primzahlen. Die Differenz
zwischen FS und ZS in je zwei Randzeilen des SQ und des
1x1-Quadrats
beträgt 27+8 = 35, zusammen 70. POPULUSQUE mit
demselben Differenzbetrag faßt beide Quadrate gewissermaßen zusammen.
Eine
weitere Gemeinsamkeit mag etwas willkürlich erscheinen, soll aber dennoch nicht
unerwähnt bleiben:
|
|
SQ |
1x1Q |
|
FW |
4 h.P |
FW |
6v.P |
FW |
|
ZS |
303 |
105 |
408 |
26 |
70 |
14 |
84 |
14 |
|
FS |
249 |
89 |
338 |
28 |
35 |
12 |
49 |
14 |
|
|
|
|
|
54 |
|
26 |
|
28 |
|
26:28
= 2*(13:14) |
||||||||
Die
Verhältniszahlen 13:14 wurden im Zusammenhang mit den ZS+FS 277 besprochen.
Statt
der geteilten Differenz 35+35 in den beiden Quadraten ist für POPULUSQUE eine
Teilung in die Konstitutivzahlen 34+36 möglich:
|
SQ |
P |
O |
U |
L |
U |
sm |
P |
U |
S |
Q |
E |
sm |
|
ZW |
15 |
14 |
20 |
11 |
20 |
80 |
15 |
20 |
18 |
16 |
5 |
74 |
|
FW |
8 |
9 |
9 |
11 |
9 |
46 |
8 |
9 |
8 |
8 |
5 |
38 |
|
|
23 |
23 |
29 |
22 |
29 |
126 |
23 |
29 |
26 |
24 |
10 |
112 |
|
80-46 = 34; 74-38 = 36;
126:112 = 14*(9:8) |
||||||||||||
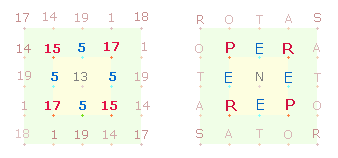
3. Das ZS-Verhältnis
84:70 der 6 vertikalen
zu den 4 horizontalen Buchstaben gibt die FS 84 und die interne Differenz 70 wieder.
In Verschiebung der Zuordnung stellen diese beide Summen eine Parallele zum
inneren Rahmen des SQ dar:
|
84 ist die ZS , 70 die FS , 14 die interne Differenz.
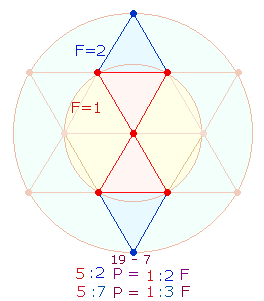
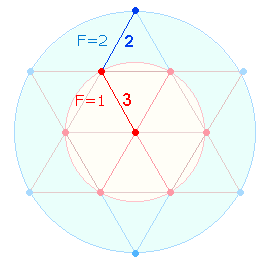
4. Das FS:ZS-Verhältnis
49:84 = 7*(7:12) der 6
vertikalen Buchstaben ist auf das Verhältnis der 5+2 Punkte der Doppelraute zu den
entsprechenden Kreisflächeneinheiten (F) zu beziehen:
|
|
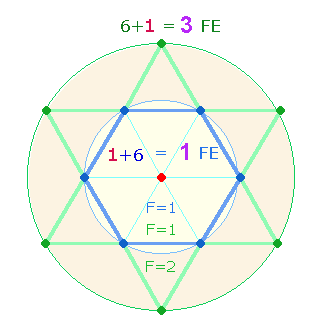
Die
Verhältniszahl 12 ist bereits vordefiniert durch
die interne Differenz 7:5 mit der
Flächenentsprechung 3:1. Das
ganze Verhältnis 7:12 gibt 3+4 = 7 Kreisflächeneinheiten
wieder, die im gemeinsamen Teilungsfaktor 7 erscheinen. Beim FS-Verhältnis 35:49 = 7*(5:7) kann man den gemeinsamen Teiler
auch als Entsprechung von 3 Flächeneinheiten zu den 1:3 Flächeneinheiten des Klammerausdrucks hinzunehmen.
5. Die ZS+FS der
Mittelpunktbuchstaben SP 33+16 = 49 ist für
sich durch 7 teilbar, was ein weiteres Verhältnis 49:84 = 7*(7:12) zu den
anderen 4 Buchstaben PVLE
ermöglicht.
Verbindet
man die Mittelpunktsbuchstaben mit den 4 horizontalen
Buchstaben, ergibt sich als ZS+FS einmal
die ZS 154 und einmal die FS 84:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
QO-VV+SP |
103 |
51 |
154 |
103 |
20 |
123 |
277 |
|
PVLE |
51 |
33 |
84 |
20 |
14 |
34 |
118 |
|
|
154 |
84 |
238 |
123 |
34 |
157 |
395 |
Von
Bedeutung ist die zweifache Summe 51, durch
die der numerische Zusammenhang der Zahl 238 an
Überzeugung gewinnt, nämlich aus der ZS 136 und der FS 102 der
Zahlen 1-16 zu bestehen.
Die
Gesamtsumme 395 = 5*79 ist, passend zu
Intention der Zahlen- und Buchstabenbelegung der DR, auf 79+5 Oktaederelemente zu beziehen. Die Summe 79 kommt
zustande durch Numerierung der DR-Elemente von 1-4, die Zahl 5 ist als
Volumen zu verstehen:
|
|
MP |
Pu. |
Li. |
Fl. |
|
|
Nummer |
1 |
2 |
3 |
4 |
|
|
Hf. |
1 |
5 |
12 |
8 |
26 |
|
sm |
1 |
10 |
36 |
32 |
79 |
Die
Einzelziffern der Zahl 157 sind
auf das Volumen des Oktaeders beziehbar, die Zahl 1 bei fehlender Numerierung, die Zahl 7 bei einer Numerierung der übrigen Elemente von 1-6.
Eine
Verrechnungsweise der Werte führt wieder zum inneren Rahmen des SQ:
|
|
ZS/FS |
FW1/2 |
sm |
FW |
|
|
238 |
157 |
395 |
84 |
|
FW |
26 |
157 |
183 |
64 |
|
sm |
|
|
|
148 |
Zweimal PR haben die ZS 64, die die FS der 4 Querlinien der DR-Kreuznumerierung 23/24 darstellt:
|
|
Die 4 E des SQ-Rahmens mit der ZS 20 bilden die
interne Differenz zwischen 64 und 84. Der beschriebene Zusammenhang ist unter
Strukturelle Aspekte des SQ ausführlich dargestellt.
1. POPULUSQUE besteht
aus 5 Konsonanten und 5 Vokalen. Auffällig sind zwei Gemeinsamkeiten
mit den geteilten 5+5 Buchstaben. Die erste besteht in den
gleichen ZS 75 und 79, die zweite in denselben ZS+FS 120 und 118, den
Konstitutivzahlen von 238:
|
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS1 |
FW |
GS2 |
|
POPUL- |
75 |
45 |
120 |
13 |
11 |
24 |
144 |
14 |
158 |
|
USQUE |
79 |
39 |
118 |
79 |
16 |
95 |
213 |
74 |
287 |
|
|
154 |
84 |
238 |
92 |
27 |
119 |
357 |
88 |
445 |
|
PPLSQ |
75 |
43 |
118 |
13 |
43 |
56 |
174 |
34 |
208 |
|
OUUUE |
79 |
41 |
120 |
79 |
41 |
120 |
240 |
16 |
256 |
|
|
154 |
84 |
238 |
92 |
84 |
176 |
414 |
50 |
464 |
Zahlenverhältnisse
von GS1, FW und GS2 ergeben
sich, wenn man jeweils die Werte der gleichen ZS+FS 120 und 118 addiert:
|
144 |
240 |
384 |
14 |
16 |
30 |
158 |
256 |
414 |
|
213 |
174 |
387 |
74 |
34 |
108 |
287 |
208 |
495 |
|
|
|
717 |
|
|
138 |
|
|
909 |
|
384:387
= 3*(128:129) = 3*257 |
||||||||
|
30:108
= 6*(5:18) = 6*23 |
||||||||
|
414:495
= 9*(46:55) = 9*101 |
||||||||
– Die Klammerzahlen des ersten Verhältnisses
sind die Konstitutiven der Zahl 257, deren
Einzelziffern die Gleichung 2+5 = 7 bilden und auf ein DR-Kreuz aus
zweimal 7 Punkten beziehbar ist. Die
Gesamtsumme 717 gibt die 15 Elemente des DR-Rahmens wieder.
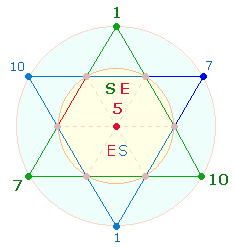
– Das Verhältnis 5:18 weist
auf die numerierte Tetraktys hin, in deren Mittelpunkt die Zahl 5 steht und deren 3
Eckwerte die Summe 18 ausmachen. Die
Buchstabenentsprechung ES – Du bist ist als eine bedeutende theologische Aussage zu
verstehen:
|
|
– Das Verhältnis 46:55 ist wohl
das erstaunlichste Ergebnis. Es gibt die FS 46 und ZS 55 der Zahlen 1-10 wieder. Der FW 107 der Summe 909 gibt die 10 Punkte der Tetraktys und 7 Punkte des Hexagons wieder. Die FW 31+22 der
Einzelsummen 414 und 495 setzen in ihren Einzelziffern
Radialelemente in Beziehung zu Kreisflächeneinheiten:
|
|
Das
wiedergegebene Kreisflächenverhältnis ist 1:2. Die
Einzelziffern der Summe 53 jedoch können für sich als
Radialelemente verstanden werden und geben dann das Flächenverhältnis 3:1 wieder.
2. Die
Zahlen 75 und 79 haben in der Kombination
offensichtlich eine besondere Bedeutung. In ihre Einzelziffern aufgeteilt
bedeuten 7+7 Punkte der beiden Tetraktyskreise das
Flächenverhältnis 1:3:
|
|
Das
Flächenverhältnis 1:3 wird
ebenfalls durch 5:9 Durchmesserelemente repräsentiert.
Die FW von 75 und 79 sind 13+79 = 92 = 4*23 = 2*46. Das Produkt 2*46 als dreistellige Zahl ist auch die Summe der 4
Einzelwerte: 75+79+13+79 = 246 = 6*41. In der Aufteilung 24+6 setzen
sich die beiden Zahlen komplementär zusammen aus (9+8+7)+(1+2+3). Die
fehlenden komplementären Zahlen 4 und 6 haben durch 92 = 2*46 zum
Ergebnis 246 beigetragen.
6*41 ist auf 3 DR beziehbar, denn von jedem äußeren Punkt einer DR lassen sich drei geometrische Figuren bilden, deren
Elemente zusammen jeweils 41 betragen:
|
|
Wenn man
für eine DR 41 nur
einmal rechnet, ist 264 auf 3 Oktaeder aus 3 DR-Kreuze beziehbar. Dies wird auch aus
der ZW/FW-Verrechnung ersichtlich:
|
|
|
|
sm |
FW |
sm |
|
ZS |
75 |
79 |
154 |
20 |
|
|
FW |
13 |
79 |
92 |
27 |
|
|
sm |
|
|
246 |
47 |
293 |
|
FW |
|
|
46 |
47 |
93 |
|
sm |
|
|
|
|
386 |
|
386 =
2*193 |
|||||
Die
Primzahl 293 ist zu verstehen als 29*3, als drei DR-Kreuze,
deren Rahmen aus jeweils 29 Elementen besteht. Die Einzelziffern der Zahl 193 geben die Punktegliederung des Tetraktyssterns wieder.
Erstellt: Januar 2013