Die
Zahlenwert/Faktorenwert-Verrechnung
I. Einleitung
II. Einzelgruppe
von 2 und mehr Zahlen
IV.a) Die dreifache Verrechnung
IV.b) Die Teilung und das Ganze
I. Einleitung
1.
Unter
den Methoden der Zahlentheorie ist die Zahlenwert/Faktorenwert-Verrechnung völlig unbekannt. Zwar ist es üblich, Zahlen
in Primzahlfaktoren zu zerlegen, doch deren Addition findet keine Beachtung oder
Verwendung. Der Bedeutung der
Faktorenwerte ist ein
eigenes Kapitel gewidmet.
Dieses bisher unbekannte Verfahren dient der
Erkenntnis von Zahlenbeziehungen und Zahlenbedeutungen. Es nutzt eine dem Zahlengefüge inhärente Eigenschaft, besitzt also
systemische Objektivität.
2.
Das im
römischen VESTA-Kult entwickelte System der Zahlenbedeutungen
verwendet die ZW/FW-Verrechnung als unerläßliches Instrument. Alle römischen
Autoren setzten sie für ihre Zahlenkonstruktionen ein.
3.
Ich habe
dieses Verfahren so weit systematisiert, daß sie zu verläßlichen Ergebnissen
einsetzbar ist. Die Vollendung des Systems sind
zukünftigen Bemühungen vorbehalten.
4.
Die
Methode ist im Grunde einfach: Es werden Einzelzahlen und deren Faktorenwerte (FW) addiert und von den Ergebnissen erneut die FW ermittelt. Hierauf weren die ersten zwei
Summen und die gefundenen FW addiert und
von beiden Summen die FW ermittelt. Eine dreimalige Durchführung
dieses Vorgangs ergibt meistens einen verwertbaren Überblick.
II. Einzelgruppe von zwei und mehr Zahlen
1. Aus praktischen Gründen seien als erstes
Beispiel zwei Zahlen, als die kleinste mögliche Zahlengruppe, verwendet:
|
|
|
|
sm |
FW |
sm |
FW |
|
Zahl |
12 |
13 |
25 |
10 |
|
|
|
FW |
7 |
13 |
20 |
9 |
|
|
|
sm |
|
|
45 |
19 |
64 |
12 |
|
FW |
|
|
11 |
19 |
30 |
10 |
|
sm |
|
|
|
|
|
22 |
Der vorstehende Verrechnungsvorgang enthält drei Additionen von FW.
Der fortlaufenden Verrechnung liegen die 4Werte zugrunde: Von einer Zahlensumme und
Faktorensumme werden wiederum die FW ermittelt:
|
ZS |
FS |
sm |
FW1 |
FW2 |
sm |
GS |
|
25 |
20 |
45 |
10 |
9 |
19 |
64 |
Der Rechenvorgang kann so lange fortgesetzt
werden, bis beide FW Primzahlen sind. Dazu ein Beispiel,
das, unabhängig von seinem konkreten
Zusammenhang, zwei Zahlen zueinander in Beziehung setzt und in der Verrechnung
zu zwei Primzahlen führt:
|
|
|
|
sm |
FW |
|
Zahl |
526 |
530 |
1056 |
24 |
|
FW |
265 |
60 |
325 |
23 |
|
sm |
|
|
1381 |
47 |
|
FW |
|
|
PZ |
PZ |
2. Als zweites Beispiel – mit Interpretation – diene die
Zahlensumme (ZS) und die Faktorensumme (FS) der Zahlen 1-49
(aus 49 Elementen besteht der Tetraktysstern):
|
|
ZS |
FS |
sm |
FW |
sm |
FW |
|
FW |
|
|
1225 |
694 |
1919 |
120 |
|
|
|
|
|
FW |
24 |
349 |
373 |
373 |
|
|
|
|
|
sm |
|
12*191 |
2292 |
493 |
2785 |
562 |
5*557 |
|
|
FW |
|
|
198 |
46 |
244 |
65 |
|
|
|
sm |
|
|
|
13*233 |
3029 |
627 |
|
|
|
FW |
|
|
|
|
246 |
33 |
279 |
37 |
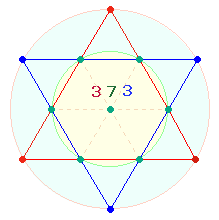
Die Summe 373 gibt eine
Punkteaufteilung des Tetraktyssterns wieder: 7 hexagonale Punkte
und jeweils 3 Eckpunkte für zwei Tetraktys:
|
|
Zur FS 694 = 2*347
= FW 349: Eine Tetraktysseite besteht aus 4 Punkten
und 3 Linien.
Zwei Erklärungsmöglichkeiten gibt es:
– Die Teilsumme 4 wird zur
Gesamtsumme 7 ins Verhältnis gesetzt.
– Eine Tetraktysseite entsteht durch
Verlängerung der 6 hexagonalen Segmentlinien. Zu den den 3 Elementen
einer Segmentlinie kommen weitere 4 Elemente hinzu, die zur
Gesamtsumme ins Verhältnis gesetzt werden.
Die Zahl 347 ist somit
als 3*(4:7) auf drei
Tetraktysseiten zu beziehen, der FW 349 als 3*4 Punkte + 9 Linien zu
verstehen.
3.
Die Durchführung
der ZW/FW-Verrechnung ist
nur sinnvoll, wenn sie in ihrer ontologischen Relevanz
interpretiert wird: Sie ist von jedem Verdacht des
"Hineininterpretierens" freizuhalten. Bei der Interpretation ist fast
immer eine beschränkte Auswahl der Erklärungen zu treffen.
Erstellt:
März 2006
Überarbeitet:
2016