Die römischen
Zahlen und die übrigen lateinischen Buchstaben (3)
und ihre Beziehung zum Dezimalsystem
A. Entwicklungen
IV. Die Zahlen 3 und 7 und ihre Zusammensetzungen
a) Die Zahl 21
b) Das Verhältnis 3:7
c) Die Zahl 37
d) 7+3
V. Die Lösung des
Geheimnisses
VI. Die Zahl 33
IV. Die Zahlen 3 und 7 und ihre Zusammensetzungen
a) Die Zahl 21
1.
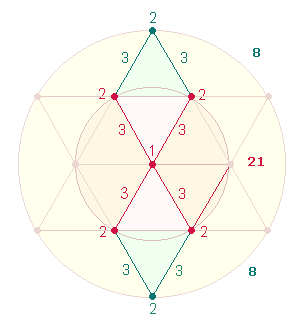
Die Bedeutung der Zahl 21 wurde im vorhergehenden
Abschnitt dargelegt. Sie besteht aus den Faktoren 3*7, die addiert den Faktorenwert (FW) 10 ergeben.
2.
Die Ziffern 2 und 1 weisen auf die 3 göttlichen Personen hin. Sie sind im
Flächenverhältnis 2:1 des äußeren Kreisrings und des inneren Kreises des Doppelkreises des
Tetraktyssterns zeichenhaft vertreten. In der Doppelraute (DR) mit ihren 21 Elementen stehen 2 Punkte für die
Flächengröße 2 und 5 Punkte für die Flächengröße 1.
3.
Dasselbe Flächenverhältnis 2:1 läßt sich auch für
die Tetraktys selbst erkennen. Denn 3 Punkte liegen auf der Kreislinie des äußeren Kreises, und aus 6+1 Punkten besteht das Hexagon. Durch
Addition erhält man für die Flächeneinheit 2 die Punktezahl 2+3 = 5 und für die
Flächeneinheit 1 5+7 = 12 Punkte. Fügt man die jeweilige
Flächengröße hinzu, ergeben sich die Zahlen 7 und 13. Die Zahl 7 vertritt nun 1 Flächeneinheit des
Hexagons, die Zahl 13 3 Flächeneinheiten des äußeren Kreises. Zählt man wiederum beide
Flächeneinheiten hinzu, erhält man das Verhältnis 8:16 = 8*(1:2). Flächenanteile und
Punkte verteilen sich nun 3+5 und 4+12.
Nehmen die drei Eckpunkte der Tetraktys noch den
Mittelpunkt hinzu, repräsentieren die Punkte 4:6 die Flächengrößen 3:1, so daß ein gleiches Verhältnis von 7:7 entsteht.
4.
Sowohl die DR als auch die Tetraktys enthalten Gliederungen nach den
Faktoren 3*7. In der DR sind es 7 Punkte und 10 Linien + 4 Dreiecke, in der
Tetraktys 3 Seitenlängen aus je 4
Punkten und 3 Linien.
Die DR läßt sich auch in 7*3 Einheiten gliedern, bestehend aus 1*3
Vertikalpunkte, 2*3 Fläche–Querlinie–Fläche
und 4*3 Linie–Punkt–Linie der
linken und rechten Seite.
1.
Das Verhältnis 3:7 ist eine
Analogbildung zum Verhältnis 1:3, das aus 1+(1+2) entsteht. Das Verhältnis
1:3 geht aus dem Flächenverhältnis des inneren zum äußeren Kreis des
Tetraktyssterns hervor und steht zeichenhaft für den einen Gott in drei
Personen. Das zweite Kreisverhältnis 1:2 berücksichtigt nur den äußeren Kreisring. Beide
Verhältnisse begründen in der jeweiligen Addition der Flächengrößen die
Bedeutung der Zahlen 4 und 3. Das Verhältnis 3:7 entsteht also aus der Rechnung 3+(3+4).
Das Verhältnis 3:4 setzt die Analogbildung der benachbarten Zahlen 1:2 fort. Am
deutlichsten ist die an der Zahl 12 erkennbar, die aus 3*4 besteht. Das
Produkt 3*7 = 21 stellt also das Verhältnis 1:3 dar.
Die Umkehrform 21 läßt auch and die Umkehrung des
Verhätnisses 1:3 zu 3:1 denken. Als zweistellige Zahlen
sind 31 und 37 die Primzahlen ihrer 10-er Reihe. Die Distichen c.85 und
c.93 des Catull bestehen jeweils aus 37 und 31 Buchstaben. Die analoge Beziehung
zwischen den beiden genannten Verhältnissen mag dabei eine Rolle spielen.
2.
Während 1:3 ein reines
Flächenverhältnis darstellt, ist dies beim Verhältnis 3:7 nicht erkennbar.
Zwei mögliche Erklärungen sind:
–
Das Verhältnis 3:4:3 bedeutet 3 Punkte der
hexagonalen Mittelachse, 4 Punkte der Achsen 2 und 3 sowie die 3 Eckpunkte der
Tetraktys. Die umgekehrte Reihenfolge ist ebenso denkbar.
–
Eine Tetraktysseite enthält 3 Linien und 4 Punkte = 7 Elemente. Um die Ganzheit der Zahl 7 auszudrücken, wird
die Teilmenge zur Gesamtzahl ins Verhältnis gesetzt.
c) 7+3
1.
Am Zustandekommen der Zahl 10 als wiederkehrender
Einheit des Dezimalsystems wirkt auch die Zahl 7 mit. Sie ist mit der Zahl 11 vergleichbar, da 7 Streckenpunkte 6 Maßeinheiten von einander
trennen, wie dies die Zahl 11 mit 10 Maßeinheiten tut. Die
Zahlen 6 und 10 sind Summen aus den Zahlen 1-3 und 1-4.
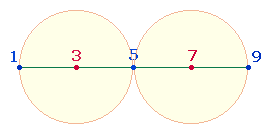
Aus 7 Punkten werden 10 Punkte, indem das Hexagon zum Tetraktysstern erweitert wird und das
Zahlendreieck der Tetraktys entsteht.
2.
Die dezimale Numerierung der DR zeigt
die Zahlen 73 in der
Mittelachse nebeneinander.
1.
Die Zahl 37 besteht aus den
Zahlen 19+18 und sind analog zu den Zahlen 9 und 8 als
Komplementärzahlen zu 1+2 zu verstehen. Ihre Berühmtheit
verdankt sie besonders den 37 Elementen der Tetraktys: 10 Punkte + 9 Dreiecke = 19 + 18 Linien. Die Zahlen 3 und 7 bilden Mittelpunkte auf der Skala der Grundzahlen 1-9:
|
|
Entsprechend stabil erweist sich die Zahl 37, wenn man ihre
Konstitutiven 19+18 verrechnet:
|
|
ZW |
FW |
Sm. |
FW |
|
|
19 |
19 |
|
|
|
|
18 |
8 |
|
|
|
Sm. |
37 |
27 |
64 |
12 |
|
FW |
37 |
9 |
46 |
25 |
|
|
|
|
|
37 |
Die Zahl 37 bleibt auch am Ende der Verrechnung
bestehen. Sie bedarf keiner anderen Erklärung, sie ist selbst Bezugspunkt anderer
Zahlen.
2.
Mittelpunkt, Punkte und Linien kann
man die Numerierung 1-2-3 geben. Der DR-Rahmen aus 15 Elementen erzielt durch diese Numerierung die Zahl 37, eine einzelne DM-Linie die Zahl 3*7 = 21:
|
|
3.
Die Zahl 37 ist zusammen mit 36 die einzige Konstitutive ihrer
Umkehrzahl 73.
V. Die Lösung
des Geheimnisses
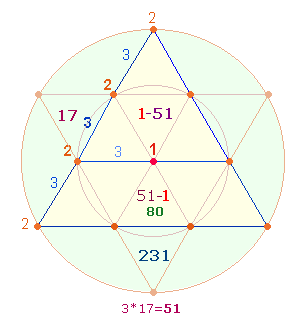
1. Numeriert man die 7 Elemente des Tetraktysrahmens mit den Zahlen 2 und 3, erhält man als Summe für die Punkte 8, für die Linien 9, zusammen die Zahl 17. Wie schon
dargelegt, sind die Zahlen 9 und 8 komplementär
zu 1 und 2 zu verstehen. Die Summe der drei
Seiten beträgt 51.
|
|
2.
Auf der Suche nach einem gleichsam göttlichen Kriterium für die Aufteilung
der ZW der Zahlzeichen und
der übrigen Buchstaben machten die Römer eine Entdeckung, wie die 7 Punkte der DR mit den 10 Punkten der Tetraktys und ihren
übrigen Elementen verbunden werden könnten: Den 3*7 = 21 Elementen des Tetraktysrahmens fehlt noch der Mittelpunkt. Durch
Hinzufügung des Mittelpunktes ergibt sich die Zahl 21-1 oder 1-21. Dieser Zahlenfolge aber
entspricht das Flächenverhältnis 3:1 des inneren Kreises zum äußeren Kreis, dessen Fläche
durch den inneren Kreis im Verhältnis 2:1 durch die Kreislinie des inneren
Kreises geteilt wird.
3.
Ähnlich kann man der numerierten
Summe 51 des Tetraktysrahmens noch den Mittelpunkt 1 hinzufügen und erhält die Zahlen 51-1 bzw. 1-51. (Die Gesamtsumme ist nun 52 = 4*13. Das Produkt 4*13 bedeutet als Gleichung 4 = 1+3. Die Zahl 4 enthält also die Einheit in der Dreiheit.) Die Tetraktys, die die göttliche Ordnung enthält, erweist sich – zusammen mit der
Doppelraute – als Ausgangspunkt der Einteilung der Zahlzeichen und Buchstaben.
Denn die Faktoren von 511 sind 7*73 und ergeben den FW 80. Betrachtet man den Faktor 7 als die Punkte des Hexagon und die Zahl 73 als 7+3 als die 10 Punkte der Tetraktys, ist das
dadurch repräsentierte Flächenverhältnis 1:3. In den Faktoren der Zahl 511 ist also die göttliche Ordnung der Zahlen in besonderer Weise
manifest und kann als Basis für die Zahlbuchstaben verwendet werden.
Grundlegender und rationaler erscheint als
Ausgangspunkt die Summe der Zahlen 1-10 = 55
= 5*11 mit der dreistelligen Zusammensetzung der Faktoren zu 511 und Umkehrung 115.
4.
Die 3 Zahlen 115, 151 und 511 haben folgende ZS+FS:
|
|
|
|
. |
Sm |
|
ZW |
115 |
151 |
511 |
777 |
|
FW |
28 |
151 |
80 |
259 |
|
|
|
|
|
1036 |
|
259:777
= 7*37*(1:3) |
||||
Zwischen der FS 259 und der ZS 777 besteht das
externe Verhältnis 1:3 und das interne 1:2, wodurch beide Flächenverhältnisse des Doppelkreises des Tetraktyssterns
in einem einzigen vereint sind.
Zieht man aus der ZS+FS 1036 die ZS+FS 396 der
Zahlen 1-21 ab, zeigt sich folgendes Verrechnungsergebnis der Teilsummen:
|
|
ZW |
FW |
Sm. |
Fakt. |
FW |
|
|
540 |
18 |
|
|
|
|
|
396 |
21 |
|
|
|
|
Sm. |
1036 |
39 |
1075 |
25*43 |
53 |
|
FW
|
48 |
16 |
64 |
|
12 |
|
|
|
|
|
|
65 |
Das Verhältnis der FW 48 und 16 ist 16*(3:1). Die Zahlen 25 und 43 ergeben in den Einzelziffern jeweils 7 und stehen
bei der Quadratbildung nebeneinander. Sie können sich auch auf die jeweils 7 Punkte der
DR und des Hexagons beziehen.
5.
Auch von den Zahlenbedeutungen der
Zahlzeichen kann man FW bilden. Die ZS+FS der Buchstabenwerte und der Zahlzeichenwerte kann man zu einer einzigen
Summe addieren. Die mit 4 mit 1 und 3 mit 5 beginnenden Zahlenbedeutungen sollen
dabei getrennt werden:
|
|
I |
X |
C |
M |
|
V |
L |
D |
|
|
ZW-Bu |
9 |
21 |
3 |
12 |
45 |
20 |
11 |
4 |
35 |
|
FW |
6 |
10 |
3 |
7 |
26 |
9 |
11 |
4 |
24 |
|
ZW-ZZ |
1 |
10 |
100 |
1000 |
1111 |
5 |
50 |
500 |
555 |
|
FW |
1 |
7 |
14 |
21 |
43 |
5 |
12 |
19 |
36 |
|
|
|
|
|
|
1225 |
|
|
|
650 |
|
1225:650 = 25*(49:26) = 25*75 |
|||||||||
Die Werte der beiden Buchstabengruppen sind
jeweils durch 25 teilbar. Die beiden Produktzahlen 25 und 75 bedeuten auf die Punkteverteilung der DR bezogen das –
oben behandelte – Flächenverhältnis 2:1 und 3:1; zu einander stehen sie im Verhältnis 1:3.
6.
Die 7 Zahlzeichen ergeben zusammen 1666 = 2*7*7*17, jedes Zahlzeichen hat also den
durchschnittlichen Wert von 17*14 = 238. Die beiden
Produktzahlen haben die Buchstabenentsprechung RO, die in ROMA und ROTA enthalten ist. Die Zahl 17 setzt sich aus den FW 7+10 der Zahlen 12 und 21 zusammen, die Zahl 14 ist der FW der
Zahlensume 33.
Der FW von 1666 ist 16+17 = 33. Die Zahl 16 gibt die Werte 1-7-1-7 des numerierten und zum Quadrat verschobenen Achsenkreuz wieder.
VII. Die Zahl 33
und weitere Erforschung des Geheimnisses
Im weiteren Verlauf dieser Untersuchung geht es immer wieder um die Zahl 33. Unter IV.b) wurde dargelegt,
daß die Zahlen 12 und 21 den
Flächenverhältnissen 1:2 und 1:3 entsprechen. Dasselbe gilt für die Zahlen 17 und 16, die die symmetrische Mitte zwischen
12 und 21 bilden. Denn sie bestehen aus den
Konstitutiven 9+8, und 9+7, den Komplementärzahlen zu 1+2 und 1+3.
Die Konstitutiven 9+7 haben ihren Ort in der Doppelzählung
der 3*3 = 9 Axialpunkte des
Hexagon, die sich bei einem Mittelpunkt auf 7 reduzieren. In der Rundumzählung der
DR-Punkte wird andererseits die Zahl 7 auf 9 erweitert,
während die Zahl 8 der Linien stets gleich bleibt.
Erstellt: März
2007