Die
römischen Zahlen und die übrigen lateinischen Buchstaben (4)
und ihre Beziehung zum Dezimalsystem
B. INNERE ZUSAMMENHÄNGE
I. Einleitung
II. Symbiose zweier Zahlengruppen
III. Die vier Werte
von Zahlensummen
IV. Berechnungen
I. Einleitung
1. Im vorhergehenden Kapitel
wurde dargelegt, daß die Zahlen 115, 151
und 511 konstitutiv für die Einteilung
der 7 Zahlzeichen (ZZ) und der 14 übrigen Buchstaben sind.
Hintergrund dafür bildet die Punkteverteilung der Doppelraute (DR) 1-5-1, aber auch eine andere Erklärung für die Zahl 151, die später gegeben wird.
2. Die folgenden
Untersuchungen führen immer wieder zur Zahl 33.
II. Symbiose zweier Zahlengruppen
Die genannten drei Zahlen gehen
mit der Zahlensumme (ZS) und Faktorensumme (FS) der Zahlen 1-21 eine Symbiose ein. Die Gründe sind hauptsächlich
folgende:
1.
Die Zahl 21 enthält die Faktoren 3*7. Die Summe der drei Zahlen 115, 151 und 511 ist 777 = 21*37. Die Summe der Zahlen 1-21 ist 21*11.
2.
Die ZS+FS haben jeweils denselben Teilungsfaktor: ZS 231 = 21*11, FS = 15*11; ZS 777 = 21*37, FS = 7*37.
3.
Die Addition beider ZS ergibt 21*(11+37) = 21*48.
Die Produktverteilung 24*42 bezieht sich insbesondere auf die beiden Tetraktysrahmen:
6*4 = 24 Punkte werden und 6*3 = 18
Linien werden zum Verhältnis 24:42, wenn man den Teil zur Gesamtzahl in Beziehung setzt. Der FW des Produkts ist 21.
III. Die vier Werte von Zahlensummen
1.
Von einer Zahl läßt sich nur deren FW ermitteln. Dies ist bei
115, 151 und 511 der Fall. Aus einer ZS läßt sich zunächst eine FS und aus beidenFW1 und FW2 bilden.
Für die Zahlen 1-21 gilt daher:
|
ZS |
FS |
Sm. |
FW1 |
FW2 |
Sm. |
GS |
|
231 |
165 |
396 |
21 |
19 |
40 |
436 |
2.
Die Teilung der Buchstaben in ZZ und übrige Buchstaben
ändert nichts an der ZS+FS ,
aber ermöglicht ein weiteres Paar von FW1 und FW2.
3.
Zunächst sollen die ZW und FW der 3 Umkehrzahlen angegeben
werden, um zu sehen, welche davon in das Buchstabensystem übernommen werden und
welche nicht:
|
ZW |
115 |
151 |
511 |
777 |
|
FW |
28 |
151 |
80 |
259 |
|
|
|
|
|
1036 |
Die 4-Werte Tabelle zeigt folgende
Werte:
|
|
ZS |
FS |
FW1 |
FW2 |
Sm. |
|
14 Bu. |
151 |
115 |
151 |
28 |
445 |
|
7 ZZ |
80 |
50 |
13 |
12 |
155 |
|
|
231 |
165 |
164 |
40 |
|
|
|
396 |
204 |
600 |
||
3 von 8 Werten des Buchstabensystems
(BuS) sind nicht von den Umkehrzahlen (UZ) übernommen: 50+13+12 = 75, während 1 von 6 Werten der Umkehrzahlen nicht am
BuS beteiligt ist: 511.
1.
Auf diese Weise ergibt sich eine Einteilung in gemeinsame
und nicht gemeinsame Zahlen, die dann einzeln und gesamt verrechnet werden:
|
BS |
525 |
75 |
600 |
|
UK |
525 |
511 |
1036 |
|
|
|
|
1636 |
Es erfolgt die Berechnung der Werte des BS und der UZ,
anschließend deren beider Ergebnisse. Bei den Zahlen 525+75, die im Verhältnis 25*(20:3) stehen fällt die Ausschließlichkeit
der Zahlen 5, 2 und 7 auf. Die runde Zahl 600 verweist durch die Produktaufteilung 25*24 auf die 49 Elemente des Tetraktyssterns:
|
|
ZW |
FW |
Sm. |
FW |
ZW |
FW |
Sm. |
FW |
||
|
|
525 |
20 |
|
|
525 |
20 |
|
|
||
|
|
75 |
13 |
|
|
511 |
80 |
|
|
||
|
Sm. |
600 |
33 |
633 |
214 |
1036 |
100 |
|
|
||
|
FW |
19 |
14 |
33 |
14 |
48 |
14 |
62 |
33 |
||
|
Sm. |
|
|
|
228 |
|
|
|
|
||
|
|
ZW |
FW |
Sm. |
FW |
|
|||||
|
|
33 |
14 |
|
|
|
|||||
|
|
62 |
33 |
|
|
|
|||||
|
Sm. |
|
47 |
|
|
|
|||||
Die 1. Verrechnung enthält zweimal die Zahl 33. Schon an dieser Stelle sei darauf
hingewiesen, daß sich die Zahlen 19 und 14 als FW von 34 und 33 verstehen lassen. In der dritten Verrechnung erscheint die Zahl
14 als FW von 33, das hier allerdings auch FW ist.
2.
Weiteren Aufschluß erhält man durch die Verrechnung der
Gesamt-ZS 1636
mit der Gesamt-FS 20+13+20+18 = 133:
|
ZS |
FS |
Sm. |
|
1636 |
133 |
|
|
413 |
26 |
439 |
Die Primzahl 439 ist am engsten auf die DR zu
beziehen. Sie besagt, daß 4*3 = 12 Außenelemente durch Hinzufügung
von 9 Vertikalelemente zur Gesamtzahl 21 gelangen. Auch auf den
Tetraktysrahmen ist diese Rechnung anwendbar, wenn man 43 als 3*4 versteht.
3.
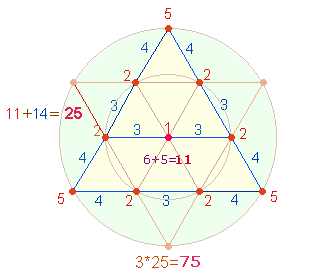
Die ZS+FS der Zahlen 1-21 ist 396. Nach Trennung der 21 Buchstaben
in ZZ und übrige Buchstaben, ergibt sich die Summe 204 der FW1 und FW2. Deren Verhältnis zur ZS+FS ist 3*4*(17:33). Die beiden Verhältniszahlen sind deshalb so bedeutsam,
da das Produkt 17*33 die Summe der Zahlen 1-33 darstellt. Deren FS ist 349.
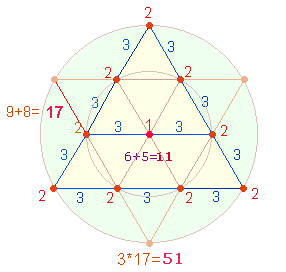
Diese Zahl bezieht sich – wie vorher schon angedeutet – auf die 3*4= 12 Punkte des Tetraktysrahmens + 9 Linien = 21 Elemente. Die Zahlen 17+16 aber bilden die Mitte zwischen 12 und 21.
Der gesamte Tetraktysrahmen
besteht aus 3*3 = 9 Linien und 3*3 = 9 Punkten. Betrachtet man jedoch nur eine
Seite, zählt man 3 Linien und 4 Punkte. Diese doppelte Sicht gilt auch für das Achsenkreuz 5 (AK5). Jede Achse besteht aus 9P+8L = 17, zusammen
34 Elementen. Da aber eine Achsenkreuz nur einen MP besitzt, entfällt ein Punkt
und die Zahl der Elemente reduziert sich auf 33.
EXKURS
3: Die Zahlen 35 und 68
4.
Ausgangspunkt für die drei Umkehrzahlen 115, 151, 511 sind die Umkehrzahlen 15 und 51. Beide werden um einen Zähler
erhöht: 15+1 = 16 und 51+1 = 52. Beide Summen ergeben 68. Auf diese Weise wird die Zahl 17 sowohl mit 3 als auch 4 multipliziert. Die Verrechnung
der ZW+FW der Zahlen 51 und 68 führt zu 33, die der Zahlen 16 und 52 zu 65:
|
ZW |
FW |
Sm. |
FW |
ZW |
FW |
Sm. |
FW |
|
51 |
20 |
|
|
16 |
8 |
|
|
|
68 |
21 |
|
|
52 |
17 |
|
|
|
119 |
41 |
160 |
15 |
68 |
25 |
93 |
34 |
|
24 |
41 |
65 |
18 |
21 |
10 |
31 |
31 |
|
|
|
|
33 |
|
|
|
65 |
Die Zahlen 33 und 65 stellen die Elemente der
Achsenkreuze 5 und 9 dar.
5.
Die zwei benachbarten Zahlenpaare 15/16 und 51/52 ergeben die trinitarischen Summen
31+103 = 134 = 2*67= FW 69.
6.
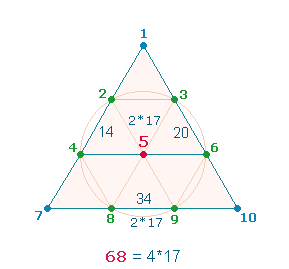
Die Beziehung zwischen 51 = 3*17 und 68 = 4*17 zeigt sich in einer zweifachen Numerierungsweise
des Tetraktysrahmens:
|
|
|
Die Zahl 51 der linken Grafik setzt sich aus 21 Positionen, die Zahl 68 der rechten aus 12 , zusammen 33 Positionen zusammen. Ohne
doppelte Zählung betragen die Summen 45+50 = 95,
die Zahl der Positionen ist 18+9 = 27. Zu den 33+27 Positionen kann man noch je 2 Mittelpunkte hinzunehmen. Die entsprechenden
Zahlensummen sind 119+6 = 125, 95+6 = 101. Die ZW/FW-Verrechnung ergibt:
|
ZW |
FW |
Sm. |
FW |
|
125 |
15 |
|
|
|
101 |
101 |
|
|
|
226 |
116 |
242 |
24 |
|
115 |
33 |
148 |
41 |
|
|
|
|
65 |
Das erste
Verrechnungsergebnis 148 weist mit den Faktoren 4*37 auf die Tetraktysseite mit 4+3 = 7 Elementen.
Wie in Exkurs 1 gezeigt, kann die Numerierung für
die Erweiterungselemente des Tetraktyssterns mit den Zahlen 4 und 5 fortgesetzt werden. Diese
Numerierung berücksichtigt die Zahl der Radial- und DM-Elemente, während die
Zahlen 1-3 mit den Flächenverhältnissen des
Tetraktyssterns in Verbindung stehen. Wegen der Parallelität der Produkte 3*17 und 4*17 erhält die Numerierung von 1-3 einen gewissen Vorzug vor der von
1-5:
|
|
Die Verbindung
dieser Numerierung mit der Tetraktysnumerierung für 33 und 27 Positionen zeigt eine eigene
Proportionalität: 75+68 = 143 = 13*11, 60+50 = 110 = 10*11. Die Gesamtsumme mit den 2*6 Mittelpunktwerten beträgt 253+12 = 265. Die Zahl 265 gibt die 13 Elemente des sanduhrförmigen
Doppeldreiecks des Hexagons wieder: 2 Dreiecke, 6 Linien, 5
Punkte. Die Zahl 11, Faktor beider Zahlenergebnisse,
ist die andere Figur im Hexagon mit 11 Elementen, die Raute.
Die Summen 226 und 265 und – ohne MP-Werte – 214 und 253 sollen nun verrechnet werden:
|
ZW |
FW |
Sm. |
FW |
ZW |
FW |
Sm. |
FW |
|
226 |
115 |
|
|
214 |
109 |
|
|
|
265 |
58 |
|
|
253 |
34 |
|
|
|
491 |
173 |
664 |
89 |
467 |
143 |
610 |
68 |
|
491 |
173 |
|
|
467 |
24 |
491 |
491 |
|
|
|
|
|
|
|
|
559 |
Die FW 173 und 89 weisen zurück auf die erste
Numerierung aus (8+9)*3
=17*3
Elementen. Die zweite Berechnung führt ebenfalls zu 491. Diese Zahl enthält die Zahlen 231 = 21*11 in der 2. Potenz. Sie kann
weiterhin verstanden werden als 49+1 und bedeutet die Hinzufügung eines 2. Mittelpunktes zu
den 49 Elementen des Tetraktyssterns.
Dieser zusätzliche Mittelpunkt reklamiert für den äußeren Kreis die
Flächengröße 3, so daß sich das bekannte Flächenverhältnis 1:3 bilden läßt.
-------------------------
7.
Die oben getrennt ermittelten 4 Werte für die 7 Zahlenbuchstaben und die übrigen 14 Buchstaben sollen hier wiederholt
werden und die Werte der Zahlzeichen hinzugefügt werden:
|
|
ZS |
FS |
FW1 |
FW2 |
Sm. |
|
14 Bu. |
151 |
115 |
151 |
28 |
445 |
|
7 ZZ |
80 |
50 |
13 |
12 |
155 |
|
Zahlen |
1666 |
79 |
33 |
79 |
1857 |
|
|
1897 |
244 |
197 |
119 |
2457 |
|
2457 = 9*13*21 = FW 29 |
|
||||
Die Zahlen 13 und 21 geben die beiden
bekannten Flächenverhältnisse wieder. Als zweistellige Zahlen bedeuten sie 13 hexagonale Elemente der DR und die
Gesamtzahl der 21 DR-Elemente. Das
dadurch repräsentierte Flächenverhältnis ist 1:3.
Die Zahlen 9 und 13 beziehen sich auf
die Elemente des Achsenkreuzes 2 und der 3 Achsen des Hexagon. Der FW 29 bedeutet
vorzugsweise die Elemente des DR-Rahmens.
Als Verhältnis des Teils zum Ganzen lassen sich die
Umkehrzahlen 34 und 43 bilden: 13+21 = 34 + 9 = 43.
8.
Es folgt nun die Verrechnung der 4 Werte der Zahlen und der 21 Buchstaben:
|
ZW |
FW |
Sm. |
FW |
|
1857 |
622 |
|
|
|
600 |
19 |
|
|
|
2457 |
641 |
3098 |
1551 |
|
29 |
641 |
670 |
74 |
|
|
|
|
1625 |
Der FW 1551 bezeugt die hohe Bedeutung der beiden 2-stelligen Umkehrzahlen,
die Zahl 670 der Zahlen 33+34. Das Endergebnis 1625 enthält als 2-stellige Zahlen die 16 Quadrate und 5*5 Punkte
des Satorquadrats. Die Faktoren 5*25*13 geben die
fünfache Summe der Zahlen 1-25 wieder. Die
Mitte des Satorquadrats wird in der Reihenfolge der Punktenumerierung durch die
Zahl 13 eingenommen, die auch der ZW des
Mittelpunkt N des SATOR-Quadrats ist.
9.
Schließlich sollen die Buchstabenwerte der Zahlzeichen mit
den durch sie bezeichneten Zahlen verbunden werden und den Werten der übrigen
14 Buchstaben entgegengestellt werden:
|
ZW |
FW |
Sm. |
FW |
|
2012 |
507 |
|
|
|
445 |
94 |
|
|
|
2457 |
601 |
3058 |
152 |
|
29 |
601 |
630 |
20 |
|
|
|
|
172 |
Der FW 152 der ZS+FS 3058 ist die Mittelpunktszahl der Zahl 303 aus 102 +201. Die Zahl 172 gibt die Punkteverteilung der Tetraktys wieder: Scheitelpunkt
des Dreiecks, 7 Hexagonalpunkte und 2 Basispunkte. Der Faktorenwert von 152 ist 4*43 = 47, das Grundverhältnis aller Umkehrzahlen.
1.
Aus den vorangehenden Darlegungen geht die besondere
Bedeutung des Tetraktysrahmens und die Numerierung der Punkte mit 2 und der Linien mit 3 hervor. Für eine Tetraktysseite
ergibt sich so die Summe 9+8 = 17 für 3 Linien und 4 Punkte. Die Summe
aller drei numerierten Seitenlängen ist 51. Diese 3*7 = 21 Positionen haben noch nicht die
Mittelpunktszahl 1 berücksichtigt. Diese kann der Zahl 21 vorangestellt oder nachgestellt
werden: 1-21, 21-1. Diese beiden Zahlen stellen das Flächenverhältnis des
Doppelkreises des Tetraktyssterns dar: 1 Einheit für den inneren Kreis, 2 Einheiten für den Kreisring des
äußeren Kreises und 1 Einheit für den inneren Kreisausschnitt. Die FW der beiden Zahlen ist 22+211 = 233, Primzahl. Es zeigt sich hier
eine Parallele zur Zahl 33, die die Summe der Umkehrzahlen 12+21 und weiterer 4 konzentrischer Paare mit der Mitte 17+16 darstellt. Nun handelt es sich um
die Zahlen 112+121. Die Faktorensumme 233 aus den Zahlen 121 und 211 hat so die dritte Umkehrzahl 112 auf den Plan gerufen.
2.
Analog zu den 21 Positionen wird nun der Zahl 51 , die Numerierungszahl 1 voran-
und nachgestellt: 1-51
und 51-1. Die FW dieser beiden Zahlen sind 151+80 = 231. Die Faktorensumme ist gleichzeitig die Zahlensumme der Zahlen 1-21.
Die Beziehung zwischen 2+1 und 5+1 besteht darin, daß
ein Radius aus 2+1 Elementen besteht, 2 Radien aber aus 2*3 bzw. aus 5
DM-Elementen und einem 2. Mittelpunkt.
Die Tetraktys mit
der genannte Numerierungsweise dient also als Richtmaß für die Summe der Buchstabenpositionen
im Alphabet, die eine bestimmte Zahl darstellen, nämlich 80 als FW von 511. Die Zahl dieser Buchstaben
richtet sich nach den 3*7
Elementen des Tetraktysrahmens und dem internen FW:ZS-Verhältnis
259*(1:2) der Umkehrzahlen 115, 151, 511. Die dritte Umkehrzahl 115 wurde als FS von 14
Buchstaben der Summe 151
bestimmt. Nun sind lediglich noch 50 Zähler als FS der 7
die Summe 80 ergebenden Buchstaben bis zur ZS+FS 231+165 = 396 übrig.
3.
Die beiden Umkehrzahlen, die die FS 231 ergeben, sollen nun noch
verrechnet werden:
|
ZW |
FW |
Sm. |
FW |
|
151 |
151 |
|
|
|
511 |
80 |
|
|
|
662 |
231 |
893 |
66 |
|
333 |
21 |
354 |
64 |
|
|
|
|
130 |
Das Verhältnis der
beiden Summanden 66:64
= 2*(33:32) gibt die 65 Elemente des Achsenkreuzes 9 wieder. Die Doppelung weist auf
die beiden konzentrischen Kreise des Tetraktysstern hin: Jeder Kreis für sich
besteht aus 2*3
Radialelementen, beide zusammen aus 2*(3+2) Radialelementen. Diesem Doppelaspekt der Radialemente
entsprechen die zwei Flächenverhältnisse 1:3 und 1:2.
Erstellt: März 2007